- 2021-11-11 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019年湖北省黄冈市中考数学模拟试卷(6月份)
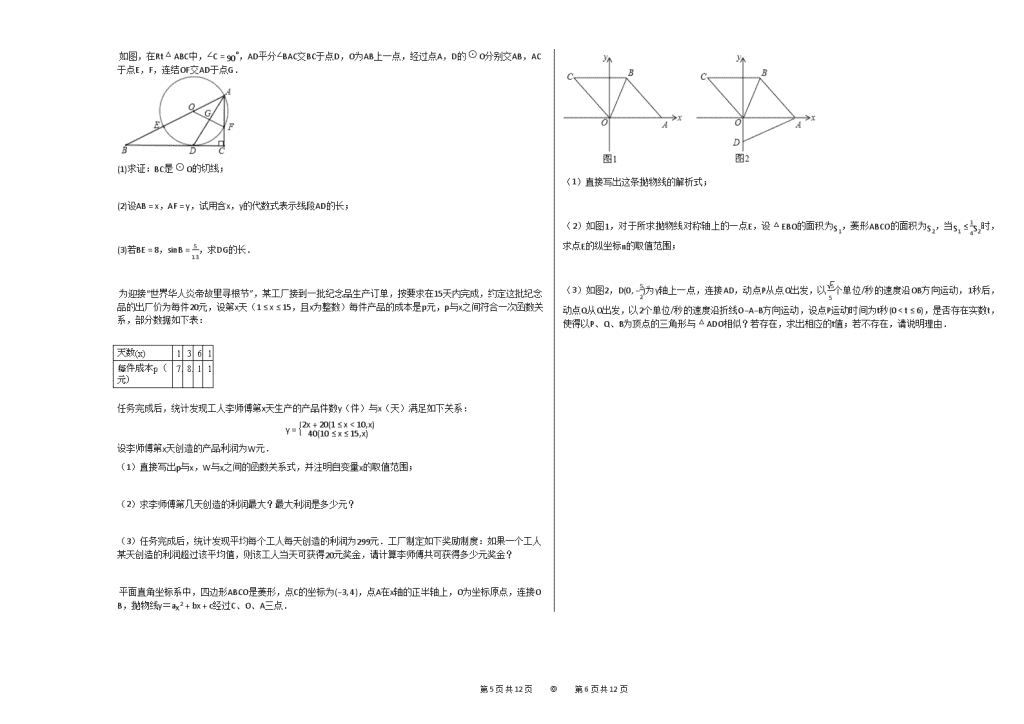
2019年湖北省黄冈市中考数学模拟试卷(6月份) 一、选择题(本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1. 比−4小2的数是( ) A.−2 B.−1 C.0 D.−6 2. 我国首艘国产航母于2018年4月26日正式下水,排水量约为65000吨,将65000用科学记数法表示为( ) A.6.5×104 B.6.5×10−4 C.−6.5×104 D.65×104 3. 下列运算正确的是( ) A.a−2=−1a2 B.a3⋅a2=a6 C.(a+2)(a−2)=a2+4 D.33−23=3 4. 下面几何体的主视图是( ) A. B. C. D. 5. 在平面直角坐标系的第二象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是( ) A.(4, −3) B.(3, −4) C.(−4, 3) D.(−3, 4) 6. 如图,若△ABC内接于半径为R的⊙O,且∠A=60∘,连接OB、OC,则边BC的长为( ) A.32R B.2R C.3R D.22R 7. 已知一组数据45,51,54,52,45,44,则这组数据的众数、中位数分别为( ) A.44,45 B.45,48 C.52,53 D.45,51 8. 如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,DN=32,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=( ) A.5.5 B.4.5 C.6 D.6.5 二、填空题(每题3分,满分24分) −12的倒数是________. 因式分解:a2(a−b)−4(a−b)=________. 计算:(−13)−1−12+3tan30∘−(π−3)0+|1−3|=________. 如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=________cm. 已知2是关于x的方程x2−2mx+3m=0的一个根,且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为________. 如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A点的最短的路线长是________. 第9页 共12页 ◎ 第10页 共12页 如图,点A是反比例函数y=4x(x>0)图象上一点,直线y=kx+b过点A并且与两坐标轴分别交于点B,C.过点A作AD⊥x轴,垂足为D,连结DC,若△BOC的面积是4,则△DOC的面积是________. A,B两地相距的路程为240千米,甲、乙两车沿同一线路从A地出发到B地,分别以一定的速度匀速行驶.甲车先出发40分钟后,乙车才出发.途中乙车发生故障,修车耗时20分钟,随后,乙车车速比发生故障前减少了10千米/小时(仍保持匀速前行),甲、乙两车同时到达B地.甲、乙两车相距的路程y(千米)与甲车行驶时间x(小时)之间的关系如图所示,求乙车修好时,甲车距B地还有________千米. 三、解答题(本大题共9小题,共72分.解答应写出文字说明、证明过程或演算步骤.) 先化简,再求值:(1+4x−2)÷x+2x2−4.其中x=3. 解分式方程:3x+1+5x−1=10x2−1 如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E. (1)求证:DE=AB. (2)以D为圆心,DE为半径作圆弧交AD于点G.若BF=FC=1,试求EG的长. 某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元? 为了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘成如图所示的频数分布直方图,已知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题: (1)图中a的值为________; (2)若要绘制该样本的扇形统计图,则成绩x在“70≤x<80”所对应扇形的圆心角度数为________度; (3)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,则获得“优秀“的学生大约有________人: (4)在这些抽查的样本中,小明的成绩为92分,若从成绩在“50≤x<60”和“90≤x<100”的学生中任选2人,请用列表或画树状图的方法,求小明被选中的概率. 如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30∘,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60∘,在斜坡上的D处测得楼顶B的仰角为45∘,其中点A,C,E在同一直线上. (1)求坡底C点到大楼距离AC的值; (2)求斜坡CD的长度. 第9页 共12页 ◎ 第10页 共12页 如图,在Rt△ABC中,∠C=90∘,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连结OF交AD于点G. (1)求证:BC是⊙O的切线; (2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长; (3)若BE=8,sinB=513,求DG的长. 为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如下表: 天数(x) 1 3 6 10 每件成本p(元) 7.5 8.5 10 12 任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系: y=2x+20(1≤x<10,x)40(10≤x≤15,x) 设李师傅第x天创造的产品利润为W元. (1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围; (2)求李师傅第几天创造的利润最大?最大利润是多少元? (3)任务完成后,统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金,请计算李师傅共可获得多少元奖金? 平面直角坐标系中,四边形ABCO是菱形,点C的坐标为(−3, 4),点A在x轴的正半轴上,O为坐标原点,连接OB,抛物线y=ax2+bx+c经过C、O、A三点. (1)直接写出这条抛物线的解析式; (2)如图1,对于所求抛物线对称轴上的一点E,设△EBO的面积为S1,菱形ABCO的面积为S2,当S1≤14S2时,求点E的纵坐标n的取值范围; (3)如图2,D(0, −52)为y轴上一点,连接AD,动点P从点O出发,以55个单位/秒的速度沿OB方向运动,1秒后,动点Q从O出发,以2个单位/秒的速度沿折线O−A−B方向运动,设点P运动时间为t秒(0查看更多
相关文章
- 当前文档收益归属上传用户