2009年北京市朝阳区中考数学一模试卷

2009年北京市朝阳区中考数学一模试卷

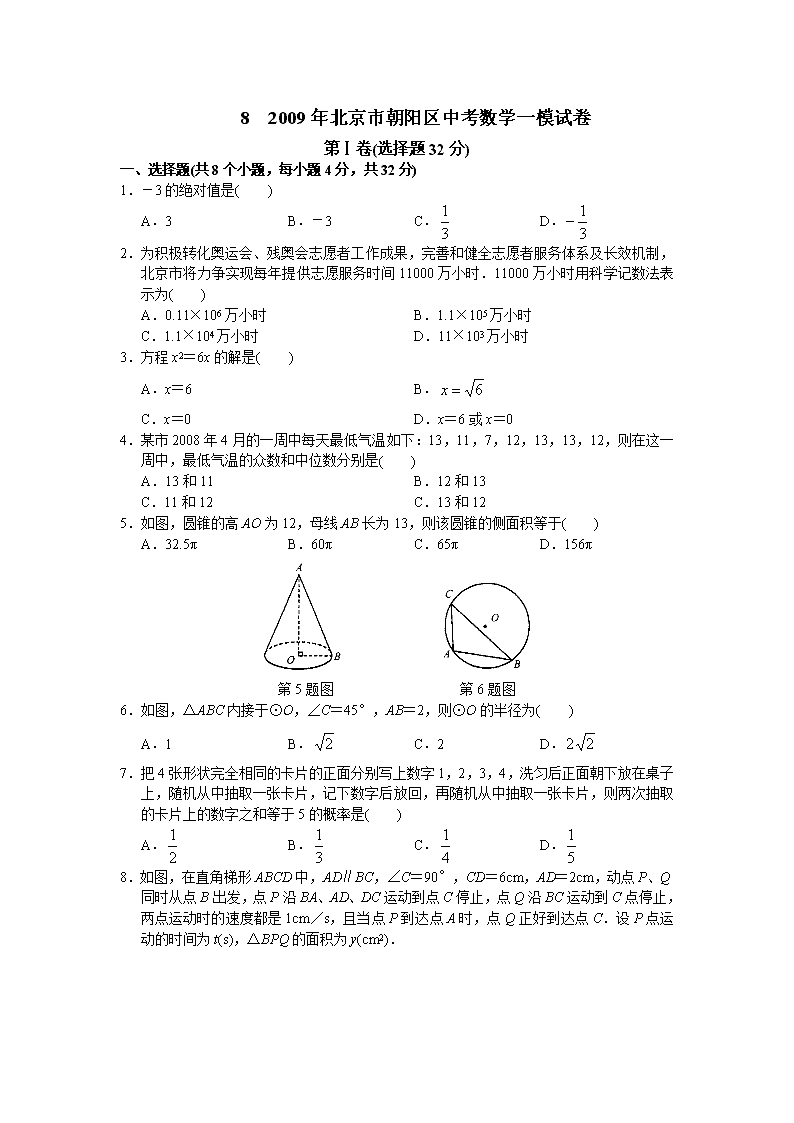
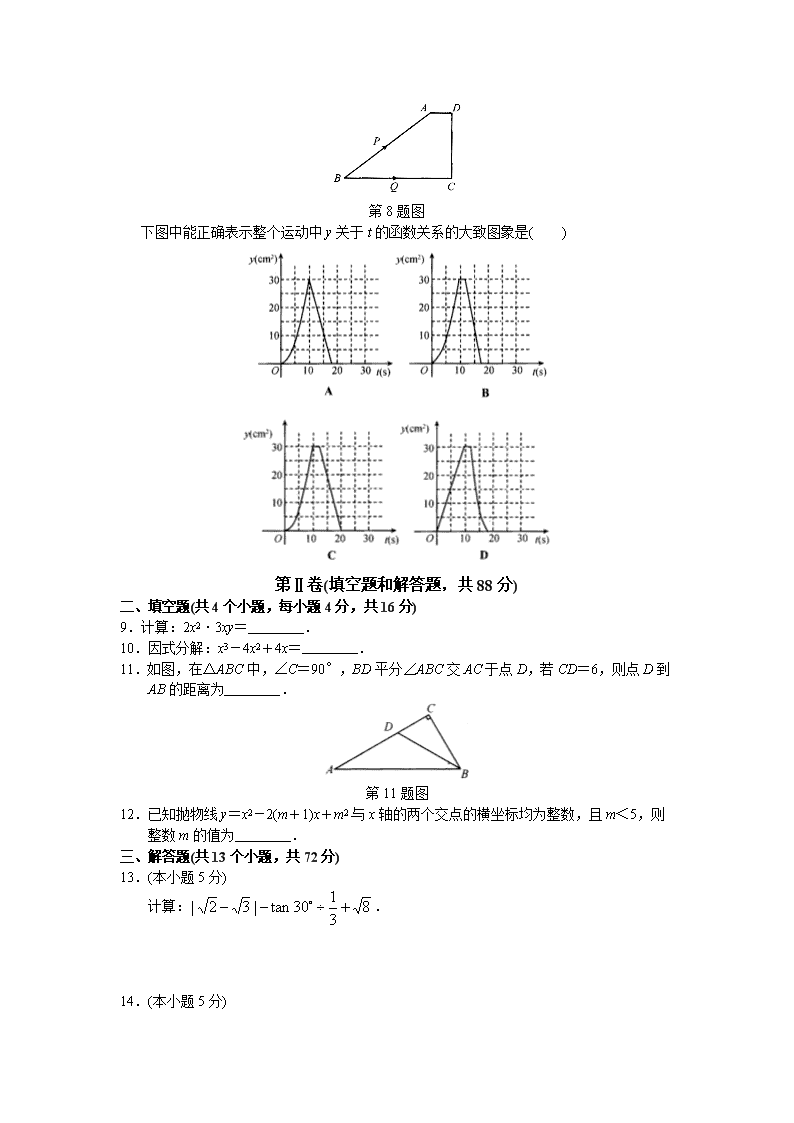
‎8 2009年北京市朝阳区中考数学一模试卷 第Ⅰ卷(选择题32分)‎ 一、选择题(共8个小题，每小题4分，共32分)‎ ‎1．－3的绝对值是( )‎ A．3 B．－‎3 ‎C． D．‎ ‎2．为积极转化奥运会、残奥会志愿者工作成果，完善和健全志愿者服务体系及长效机制，北京市将力争实现每年提供志愿服务时间11000万小时．11000万小时用科学记数法表示为( )‎ A．0.11×106万小时 B．1.1×105万小时 C．1.1×104万小时 D．11×103万小时 ‎3．方程x2＝6x的解是( )‎ A．x＝6 B．‎ C．x＝0 D．x＝6或x＝0‎ ‎4．某市2008年4月的一周中每天最低气温如下：13，11，7，12，13，13，12，则在这一周中，最低气温的众数和中位数分别是( )‎ A．13和11 B．12和13‎ C．11和‎12 ‎ C．13和12‎ ‎5．如图，圆锥的高AO为12，母线AB长为13，则该圆锥的侧面积等于( )‎ A．32.5π B．60π C．65π D．156π ‎ ‎ 第5题图 第6题图 ‎6．如图，△ABC内接于⊙O，∠C＝45°，AB＝2，则⊙O的半径为( )‎ A．1 B． C．2 D．‎ ‎7．把4张形状完全相同的卡片的正面分别写上数字1，2，3，4，洗匀后正面朝下放在桌子上，随机从中抽取一张卡片，记下数字后放回，再随机从中抽取一张卡片，则两次抽取的卡片上的数字之和等于5的概率是( )‎ A． B． C． D．‎ ‎8．如图，在直角梯形ABCD中，AD∥BC，∠C＝90°，CD＝‎6cm，AD＝‎2cm，动点P、Q同时从点B出发，点P沿BA、AD、DC运动到点C停止，点Q沿BC运动到C点停止，两点运动时的速度都是‎1cm／s，且当点P到达点A时，点Q正好到达点C．设P点运动的时间为t(s)，△BPQ的面积为y(cm2)．‎ 第8题图 下图中能正确表示整个运动中y关于t的函数关系的大致图象是( )‎ 第Ⅱ卷(填空题和解答题，共88分)‎ 二、填空题(共4个小题，每小题4分，共16分)‎ ‎9．计算：2x2·3xy＝________．‎ ‎10．因式分解：x3－4x2＋4x＝________．‎ ‎11．如图，在△ABC中，∠C＝90°，BD平分∠ABC交AC于点D，若CD＝6，则点D到AB的距离为________．‎ 第11题图 ‎12．已知抛物线y＝x2－2(m＋1)x＋m2与x轴的两个交点的横坐标均为整数，且m＜5，则 整数m的值为________．‎ 三、解答题(共13个小题，共72分)‎ ‎13．(本小题5分)‎ 计算：．‎ ‎14．(本小题5分)‎ 解方程：．‎ ‎15．(本小题5分)‎ 先化简，再求值：，其中a＝－1．‎ ‎16．(本小题5分)‎ 已知：如图，AD∥BC，AD＝BC，E为BC上一点，且AE＝AB．‎ 求证：DE＝AC．‎ 第16题图 ‎17．(本小题5分)如图，反比例函数的图象与直线y＝x－2交于点A，且A点纵坐标为1，求该反比例函数的解析式．‎ 第17题图 ‎18．(本小题5分)通常情况居民一周时间可以分为常规工作日(周一至周五)和常规休息日(周六和周日)．居民一天的时间可以划分为工作时间、个人生活必需时间、家务劳动时间和可以自由支配时间等四部分．2008年5月，北京市统计局在全市居民家庭中开展了时间利用调查，并绘制了统计图：‎ 第18题图 ‎(1)由图①调查表明，我市居民人均常规工作日工作时间占一天时间的百分比为________；‎ ‎(2)调查显示，看电视、上网、健身游戏、读书看报是居民在可自由支配时间中的主要活动方式，其中平均每天上网占可自由支配时间的12％，比读书看报的时间多8分钟．请根据以上信息补全图②；‎ ‎(3)由图②调查表明，我市居民在可自由支配时间中看电视的时间最长．根据这一信息，请你在可自由支配时间的利用方面提出一条建议：________．‎ ‎19．(本小题5分)‎ 如图，在梯形ABCD中，AB∥CD，∠D＝90°，CD＝4，∠ACB＝∠D，tanB＝求梯形ABCD的面积．‎ 第19题图 ‎20．列方程(组)解应用题(本小题5分)‎ 改革开放30年来，我国的文化事业得到了长足发展，以公共图书馆和博物馆为例，1978年全国两馆共约有1550个，至2008年已发展到约4650个．2008年公共图书馆的数量比1978年公共图书馆数量的2倍还多350个，博物馆的数量是1978年博物馆数量的5倍．2008年全国公共图书馆和博物馆各有多少个?‎ ‎21．(本小题5分)‎ 响应“绿色环保，畅通出行”的号召，越来越多的市民选择乘地铁出行，为保证市民方便出行，我市新建了多条地铁线路，与旧地铁线路相比，新建地铁车站出入口上下楼梯的高度普遍增加，已知原楼梯BD长‎20m，在楼梯水平长度(BC)不发生改变的前提下，楼梯的倾斜角由30°增大到45°，那么新修建的楼梯高度将会增加多少?‎ ‎(结果保留整数，参考数据：≈1.414，≈1.732)‎ 第21题图 ‎22．(本小题7分)‎ 已知：如图在⊙O中，AB是直径，AC是弦，OE⊥AC于点E，过点C作直线FC，使∠FCA＝∠AOE，交AB的延长线于点D．‎ ‎(1)求证：FD是⊙O的切线；‎ ‎(2)设OC与BE相交于点G，若OG＝2，求⊙O半径的长；‎ ‎(3)在(2)的条件下，当OE＝3时，求图中阴影部分的面积．‎ 第22题图 ‎23．(本小题5分)‎ 将图①，将一张直角三角形纸片ABC折叠，使点A与点C重合，这时DE为折痕，则△CBE为等腰三角形；再继续将纸片沿△CBE的对称轴EF折叠，这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形)，我们称这样两个矩形为“叠加矩形”．‎ 第23题图 ‎(1)如图②，正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能，请在图②中画出折痕；‎ ‎(2)如图③，在正方形网格中，以给定的BC为一边，画出一个斜三角形ABC，使其顶点A在格点上，且△ABC折成的“叠加矩形”为正方形；‎ ‎(3)如果一个三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是________；‎ ‎(4)如果一个四边形一定能折成“叠加矩形”，那么它必须满足的条件是________．‎ ‎24．(本小题7分)‎ 抛物线与x轴交于A(－1，0)、B两点，与y轴交于点C(0，－3)，抛物线顶点为M，连结AC并延长AC交抛物线对称轴于点Q，且点Q到x轴的距离为6．‎ ‎(1)求此抛物线的解析式；‎ ‎(2)在抛物线上找一点D，使得DC与AC垂直，求出点D的坐标；‎ ‎(3)抛物线对称轴上是否存在一点P，使得S△PAM＝3S△ACM，若存在，求出P点坐标；若不存在，请说明理由．‎ ‎25．(本小题8分)‎ 第25题图 ‎(1)已知：如图①，Rt△ABC中，∠ACB＝90°，AC＝BC，点D、E在斜边AB上，且∠DCE＝45°．求证：线段DE、AD、EB总能构成一个直角三角形；‎ ‎(2)已知：如图②，等边三角形ABC中，点D、E在边AB上，且∠DCE＝30°，请你找出一个条件，使线段DE、AD、EB能构成一个等腰三角形，并求出此时等腰三角形顶角的度数；‎ ‎(3)在(1)的条件下，如果AB＝10，求BD·AE的值．‎ 答 案 ‎8．2009年北京市朝阳区中考数学一模试卷 一、选择题 ‎1．A 2．C 3．D 4．D 5．C 6．B 7．C 8．B 二、填空题 ‎9．6x3y 10．x(x－2)2 11．6 12．0或4‎ 三、解答题 ‎13．解：原式 ‎14．解：x＝3(x－2)‎ x＝3x－6，‎ 解得x＝3．‎ 经检验，x＝3是原分式方程的解．‎ ‎15．解：原式．‎ 当a＝－1时，原式．‎ ‎16．证明：∵AD∥BC，∴∠DAE＝∠1．‎ 第16题答图 ‎∵AE＝AB，‎ ‎∴∠1＝∠B．‎ ‎∴∠B＝∠DAE．‎ 又AD＝BC，‎ ‎∴△ABC≌△AED．‎ ‎∴DE＝AC．‎ ‎17．解：把y＝1代入y＝x－2，得x＝3.‎ ‎∴点A的坐标为(3，1)．‎ 把点A(3，1)代入，得k＝3．‎ ‎∴该反比例函数的解析式为．‎ ‎18．解：(1)31.6％：‎ ‎(2)补全统计图：‎ 第18题答图 ‎(说明：本问共3分，①补全“上网”给1分；②补全“健身游戏”给2分．)‎ ‎(3)答案不唯一，如：适当减少看电视的时间，多做运动，有益健康．(合理即给分)‎ ‎19．解：在梯形ABCD中，AB∥CD，‎ 第19题答图 ‎∴∠1＝∠2．‎ ‎∵∠ACB＝∠D＝90°．‎ ‎∴∠3＝∠B．‎ ‎．‎ 在Rt△ACD中，CD＝4，‎ ‎．‎ ‎．‎ 在Rt△ACB中，，‎ ‎．‎ ‎.‎ ‎20．解：设1978年全国有公共图书馆x个，博物馆y个，‎ 由题意，得 解得 则2x＋350＝2650，5y＝2000．‎ 答：2008年全国有公共图书馆2650个，博物馆2000个．‎ ‎21．解：由题意，可得△ABC和△BDC都是直角三角形，‎ 在Rt△BDC中，BD＝20，∠DBC＝30°，‎ ‎，．‎ 在Rt△ABC中，∠ABC＝45°，‎ ‎∴AC＝BC＝10．‎ ‎∴AD＝AC－CD＝10－10．‎ ‎∴AD≈7(m)．‎ 答：新修建的楼梯高度会增加‎7米．‎ ‎22．证明：(1)连结OC(如图①)，‎ ‎①‎ ‎②‎ 第22题答图 ‎∵OA＝OC．∴∠1＝∠A．‎ ‎∵OE⊥AC．∴∠A＋∠AOE＝90°．‎ ‎∴∠1＋∠AOE＝90°．‎ 又∠FCA＝∠AOE，‎ ‎∴∠1＋∠FCA＝90°．即∠OCF＝90°．‎ ‎∴FD是⊙O的切线．‎ ‎(2)连结BC(如图②)，‎ ‎∵OE⊥AC，∴AE＝EC．‎ 又AO＝OB，‎ ‎∴OE∥BC且．‎ ‎∴△OEG∽△CBG．‎ ‎．‎ ‎∴OG＝2，∴CG＝4．‎ ‎∴OC＝6．‎ 即⊙O半径是6．‎ ‎(3)∵OE＝3，由(2)知BC＝2OE＝6．‎ ‎∵OB＝OC＝6，‎ ‎∴△OBC是等边三角形．‎ ‎∴∠COB＝60°．‎ 在Rt△OCD中，CD＝OC·tan60°＝6，‎ ‎∴S阴＝S△OCD－S扇OBC ‎＝18－6p ．‎ ‎23．(1) (2)‎ ‎ ‎ ‎① ②‎ ‎(说明：只需画出折痕．)‎ 第23题答图 ‎(说明：只需画出满足条件的一个三角形；答案不唯一，所画三角形的一边长与该边上的高相等即可．)‎ ‎(3)三角形的一边长与该边上的高相等．‎ ‎(4)对角线互相垂直．(注：回答菱形、正方形不给分)‎ ‎24．解：(1)设直线AC的解析式为y＝kx－3，把A(－1，0)代入得k＝－3．‎ ‎∴直线AC的解析式为y＝－3x－3．‎ 依题意知，点Q的纵坐标是－6．‎ 把y＝－6代入y＝－3x－3中，解得x＝1，∴点Q(1，－6)．‎ ‎∵点Q在抛物线的对称轴上，‎ ‎∴抛物线的对称轴为直线x＝1．‎ 设抛物线的解析式为y＝a(x－1)2＋n，‎ 由题意，得解得 ‎∴抛物线的解析式为y＝(x－1)2－4．‎ ‎(2)如图①，过点C作AC的垂线交抛物线于点D，交x轴于点N，则∠ACO＝∠ANC，‎ ‎∴tan∠ANC＝tan∠ACO，．‎ ‎∵OA＝1，OC＝3，∴ON＝9．‎ ‎∴点N的坐标为(9，0)．‎ 可求得直线CN的解析式为．‎ 由解得 即点D的坐标为．‎ ‎ ‎ ‎① ②‎ 第24题答图 ‎(3)设抛物线的对称轴交x轴于点E，‎ 依题意，得AE＝2，EM＝4，AM＝2．‎ ‎∵S△ACM＝S△AOC＋S梯形OCME－S△AME＝1，‎ 且，‎ 又∵S△PAM＝3S△ACM，∴PM＝3．‎ 设P(1，m)，‎ ‎①当点P在点M上方时，PM＝m＋4＝3，‎ ‎∴m＝－1，∴P(1，－1)．‎ ‎②当点P在点M下方时，PM＝－4－m＝3，‎ ‎∴m＝－7，∴P(1，－7)．‎ 综上所述，点P的坐标为P1(1，－1)，P2(1，－7)．‎ ‎25．(1)证明：如图①，∵∠ACB＝90°，AC＝BC，‎ ‎∴∠A＝∠B＝45°．‎ 以CE为一边作∠ECF＝∠ECB，在CF上截取CF＝CB，则CF＝BC＝AC．‎ 连结DF、EF，则△CFE≌△CBE．‎ ‎∴FE＝BE，∠1＝∠B＝45°．‎ ‎∵∠DCE＝∠ECF＋∠DCF＝45°，‎ ‎∴∠DCA＋∠ECB＝45°．‎ ‎∵∠DCF＝∠DCA．‎ ‎∴△DCF≌△DCA．‎ ‎∴∠2＝∠A＝45°，DF＝AD．‎ ‎∴∠DFE＝∠2＋∠1＝90°．‎ ‎∴△DFE是直角三角形．‎ 又AD＝DF，EB＝EF，‎ ‎∴线段DE、AD、EB能构成一个直角三角形．‎ ‎ ‎ ‎① ②‎ 第25题答图 ‎(2)当AD＝BE时，线段DE、AD、EB能构成一个等腰三角形．‎ 如图②，与(1)类似，以CE为一边，作∠ECF＝∠ECB，在CF上截取CF＝CB，可得△CFE≌△CBE，△DCF≌△DCA．‎ ‎∴AD＝DF，EF＝BE．‎ ‎∴∠DFE＝∠1＋∠2＝∠A＋∠B＝120°．‎ 若使△DFE为等腰三角形，只需DF＝EF，即AD＝BE．‎ ‎∴当AD＝BE时，线段DE、AD、EB能构成一个等腰三角形．‎ 且顶角∠DFE为120°．‎ ‎(3)证明：如图①，‎ ‎∵∠ACE＝∠ACD＋∠DCE，∠CDB＝∠ACD＋∠A．‎ 又∠DCE＝∠A＝45°，‎ ‎∴∠ACE＝∠CDB．‎ 又∠A＝∠B，‎ ‎∴△ACE∽△BDC．‎ ‎．‎ ‎∴BD·AE＝AC·BC．‎ ‎∵Rt△ACB中，由AC2＋BC2＝AB2＝102，得AC2＝BC2＝50．‎ ‎∴BD·AE＝AC·BC＝AC2＝50．‎ 说明：各解答题不同的正确解法参照以上标准给分．‎