- 2021-11-11 发布 |
- 37.5 KB |
- 11页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019九年级数学上册 专题突破讲练 与圆有关的动态问题试题 (新版)青岛版
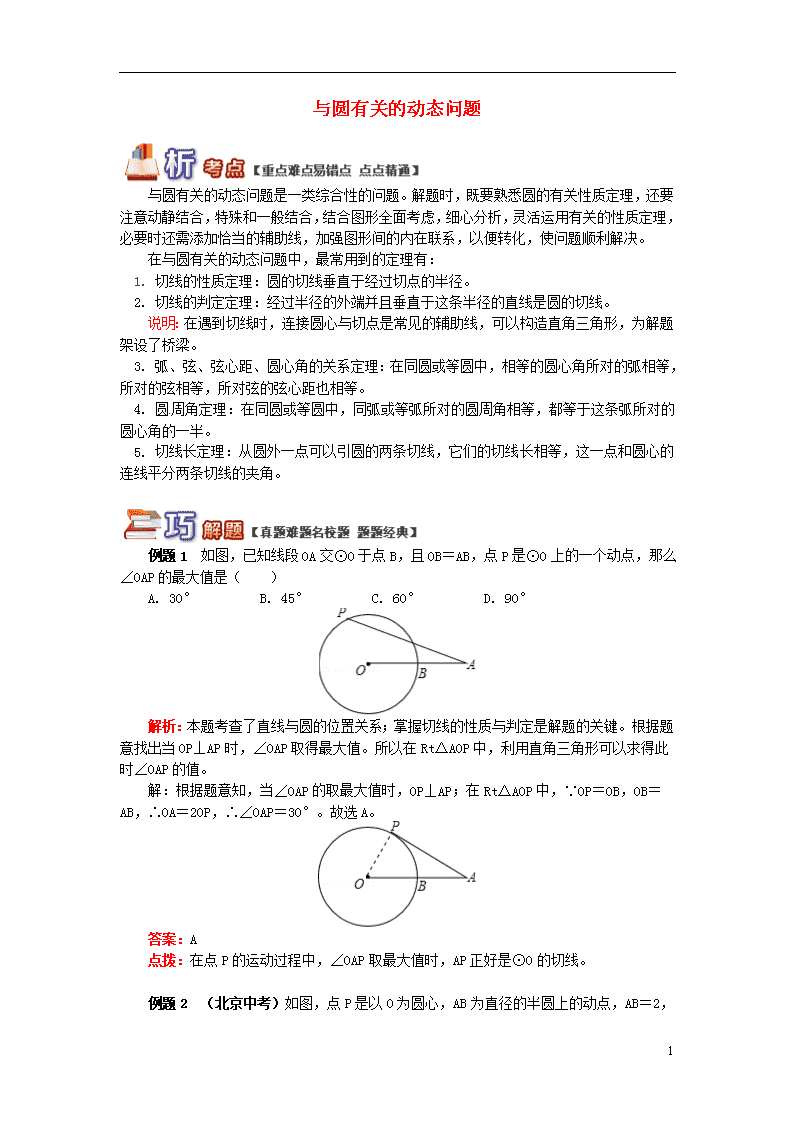
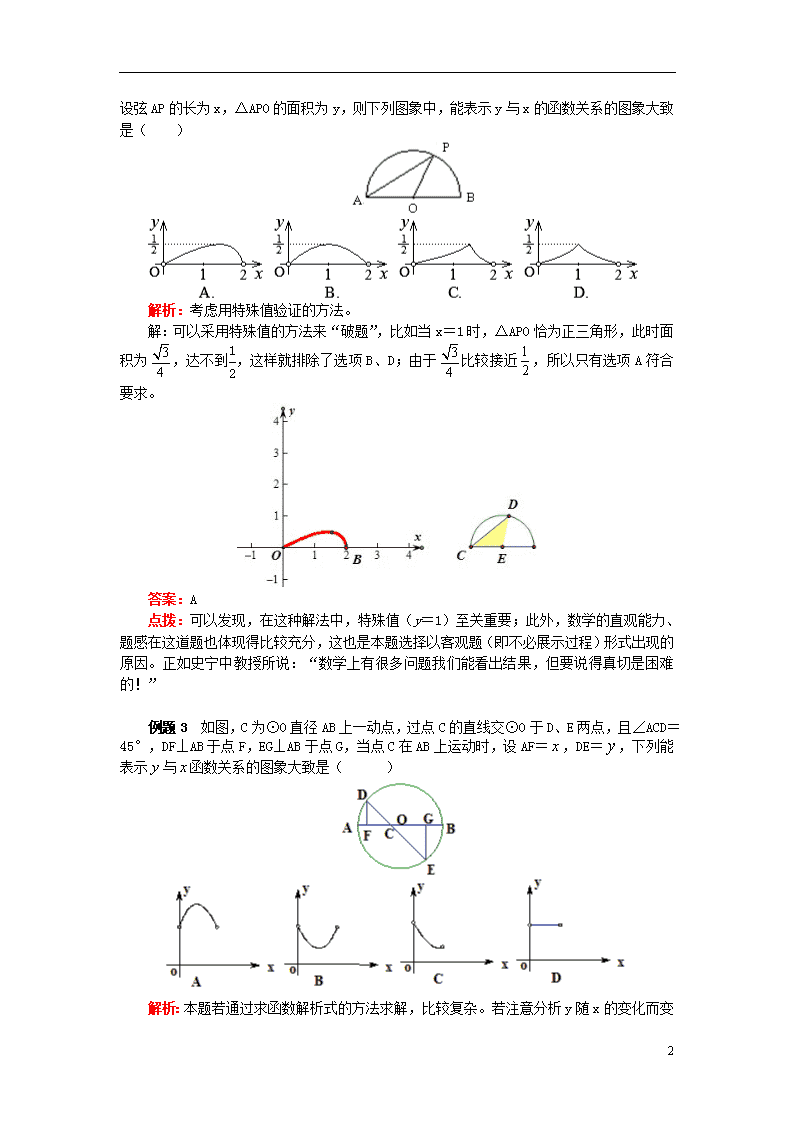
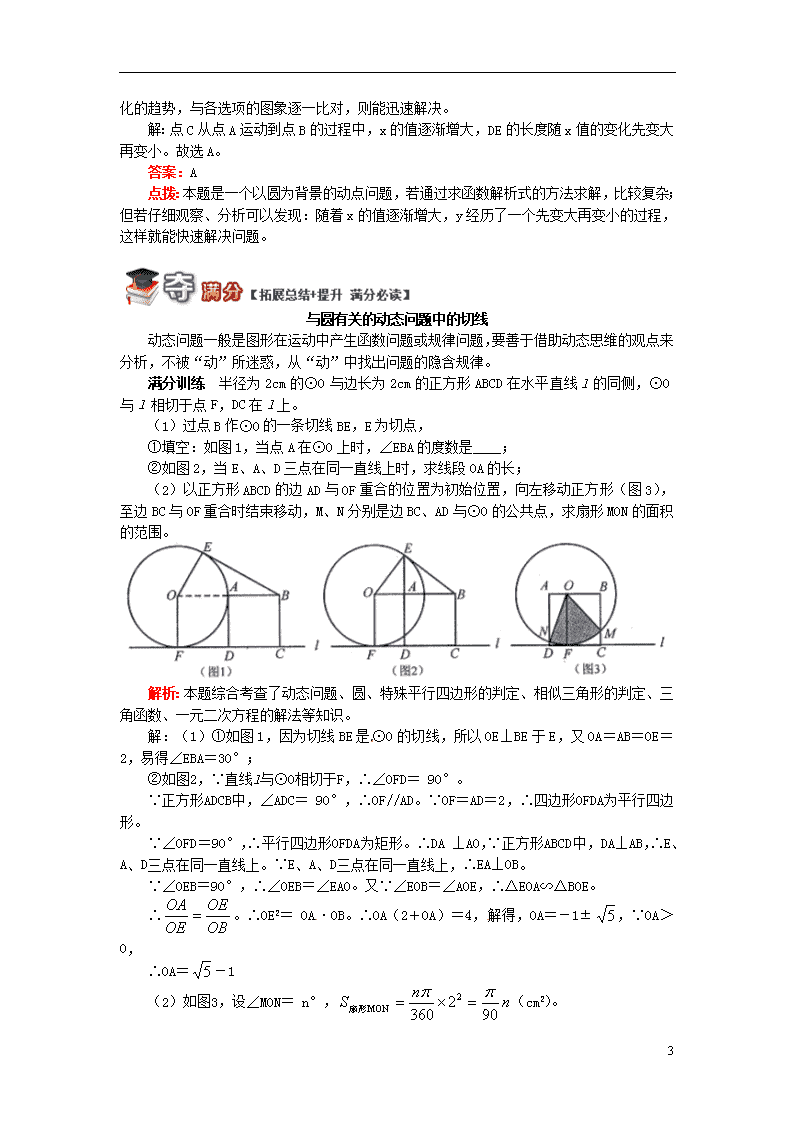
与圆有关的动态问题 与圆有关的动态问题是一类综合性的问题。解题时,既要熟悉圆的有关性质定理,还要注意动静结合,特殊和一般结合,结合图形全面考虑,细心分析,灵活运用有关的性质定理,必要时还需添加恰当的辅助线,加强图形间的内在联系,以便转化,使问题顺利解决。 在与圆有关的动态问题中,最常用到的定理有: 1. 切线的性质定理:圆的切线垂直于经过切点的半径。 2. 切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。 说明:在遇到切线时,连接圆心与切点是常见的辅助线,可以构造直角三角形,为解题架设了桥梁。 3. 弧、弦、弦心距、圆心角的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距也相等。 4. 圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。 5. 切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。 例题1 如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( ) A. 30° B. 45° C. 60° D. 90° 解析:本题考查了直线与圆的位置关系;掌握切线的性质与判定是解题的关键。根据题意找出当OP⊥AP时,∠OAP取得最大值。所以在Rt△AOP中,利用直角三角形可以求得此时∠OAP的值。 解:根据题意知,当∠OAP的取最大值时,OP⊥AP;在Rt△AOP中,∵OP=OB,OB=AB,∴OA=2OP,∴∠OAP=30°。故选A。 答案:A 点拨:在点P的运动过程中,∠OAP取最大值时,AP正好是⊙O的切线。 例题2 (北京中考) 11 如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( ) 解析:考虑用特殊值验证的方法。 解:可以采用特殊值的方法来“破题”,比如当x=1时,△APO恰为正三角形,此时面积为,达不到,这样就排除了选项B、D;由于比较接近,所以只有选项A符合要求。 答案:A 点拨:可以发现,在这种解法中,特殊值(y=1)至关重要;此外,数学的直观能力、题感在这道题也体现得比较充分,这也是本题选择以客观题(即不必展示过程)形式出现的原因。正如史宁中教授所说:“数学上有很多问题我们能看出结果,但要说得真切是困难的!” 例题3 如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=,DE=,下列能表示与函数关系的图象大致是( ) 解析: 11 本题若通过求函数解析式的方法求解,比较复杂。若注意分析y随x的变化而变化的趋势,与各选项的图象逐一比对,则能迅速解决。 解:点C从点A运动到点B的过程中,x的值逐渐增大,DE的长度随x值的变化先变大再变小。故选A。 答案:A 点拨:本题是一个以圆为背景的动点问题,若通过求函数解析式的方法求解,比较复杂;但若仔细观察、分析可以发现:随着x的值逐渐增大,y经历了一个先变大再变小的过程,这样就能快速解决问题。 与圆有关的动态问题中的切线 动态问题一般是图形在运动中产生函数问题或规律问题,要善于借助动态思维的观点来分析,不被“动”所迷惑,从“动”中找出问题的隐含规律。 满分训练 半径为2cm的⊙O与边长为2cm的正方形ABCD在水平直线l的同侧,⊙O与l 相切于点F,DC在l上。 (1)过点B作⊙O的一条切线BE,E为切点, ①填空:如图1,当点A在⊙O上时,∠EBA的度数是____; ②如图2,当E、A、D三点在同一直线上时,求线段OA的长; (2)以正方形ABCD的边AD与OF重合的位置为初始位置,向左移动正方形(图3),至边BC与OF重合时结束移动,M、N分别是边BC、AD与⊙O的公共点,求扇形MON的面积的范围。 解析:本题综合考查了动态问题、圆、特殊平行四边形的判定、相似三角形的判定、三角函数、一元二次方程的解法等知识。 解:(1)①如图1,因为切线BE是⊙O的切线,所以OE⊥BE于E,又OA=AB=OE=2,易得∠EBA=30°; ②如图2,∵直线l与⊙O相切于F,∴∠OFD= 90°。 ∵正方形ADCB中,∠ADC= 90°,∴OF//AD。∵OF=AD=2,∴四边形OFDA为平行四边形。 ∵∠OFD=90°,∴平行四边形OFDA为矩形。∴DA ⊥AO,∵正方形ABCD中,DA⊥AB,∴E、A、D三点在同一直线上。∵E、A、D三点在同一直线上,∴EA⊥OB。 ∵∠OEB=90°,∴∠OEB=∠EAO。又∵∠EOB=∠AOE,∴△EOA∽△BOE。 ∴。∴OE2= OA·OB。∴OA(2+OA)=4,解得,OA=-1±,∵OA>0, ∴OA=-1 (2)如图3,设∠MON= n°,(cm2)。 11 S随n的增大而增大,∠MON取最大值时,最大。 过O点作OK⊥MN于K,∴∠MON=2∠NOK,NM=2NK, 在Rt△ONK中,sin∠NOK= ∴∠NOK随NK的增大而增大,∠MON随MN的增大而增大,∴当MN最大时∠MON最大,当MN最小时∠MON最小。 ①当N、M、O分别与D、B、A重合时,MN最大,MN=BD,∠MON=∠BOD=90°,(cm2) ② 当MN=DC=2时,MN最小。 ∴ON=MN=OM,∴∠NOM=60°。 (cm2),∴。 答案:(1)30°;-1;(2) 点拨:这类问题可细分为点动型、线动型、形动型。解答这类问题时,要求对几何元素的运动过程有一个完整、清晰的认识,不管点动、线动还是形动,从特殊情形入手,变中求不变,动中求静,抓住静的瞬间,把动态的问题转化为静态的问题来解决,从而找到“动”与“静”的联系,揭示问题的本质,发现运动中的各个变量之间互相依存的函数关系,从而找到解决问题的突破口,也就找到了解决这类问题的途径。 (答题时间:45分钟) 【友情提示】因本讲内容综合性较强,故在解题过程中可能会涉及到相似和锐角三角函数相关知识,请敢于挑战自我、勇于得满分的“童鞋”提前预习相关知识点。 1. 如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD上移动。当∠APB的度数最大时,则∠ABP的度数为( ) A. 15° B. 30° C. 60° D. 90° 2.(湖南中考)如图所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过的时间为t,正方形除去圆部分的面积为S(阴影部分),则S与t的大致图象为( ) 11 A. B. C. D. 3. (甘肃中考)如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为( ) *4. (甘肃中考)如图,已知⊙P的圆心在定角(0°<<180°) 的角平分线上运动,且⊙P与的两边相切,则图中阴影部分的面积S关于⊙P的半径r(r>0)变化的函数图象大致是( ) 5. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于的函数图像大致是( ) 11 A. B. C. D. 6. 如图,A、B、C、D为⊙O的四等分点,动点P从圆心O出发,沿OC→→DO的路线做匀速运动,设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y(度)与t(秒)的函数关系最恰当的是( ) A. B. C. D. 7. 如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( ) A. 2周 B. 3周 C. 4周 D. 5周 8. 如图,△ABC中,∠BAC=60°,∠ABC =45°,AB=2,D 是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 。 9. 如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,∠AOB=45°,点P在x轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P(x,0),则x的取值范围是________。 11 *10. 如图,∠APB=30°,圆心在边PB上的⊙O半径为1cm,OP=3cm,若⊙O沿BP方向移动,当⊙O与PA相切时,求圆心O移动的距离。 ***11. 在矩形ABCD中,点P是边AD上的动点,连接BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,连接QP(如图)。已知AD=13,AB=5,设AP=x,BQ=y。 (1)求y关于x的函数解析式,并写出x的取值范围; (2)当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时,求的值; (3)点E在边CD上,过点E作直线QP的垂线,垂足为F,如果EF=EC=4,求x的值。 ***12. 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6)。动点Q从点O、动点P从点A同时出发,分别沿OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0查看更多
相关文章
- 当前文档收益归属上传用户