- 2021-11-11 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学总复习专题课件:两圆相切2
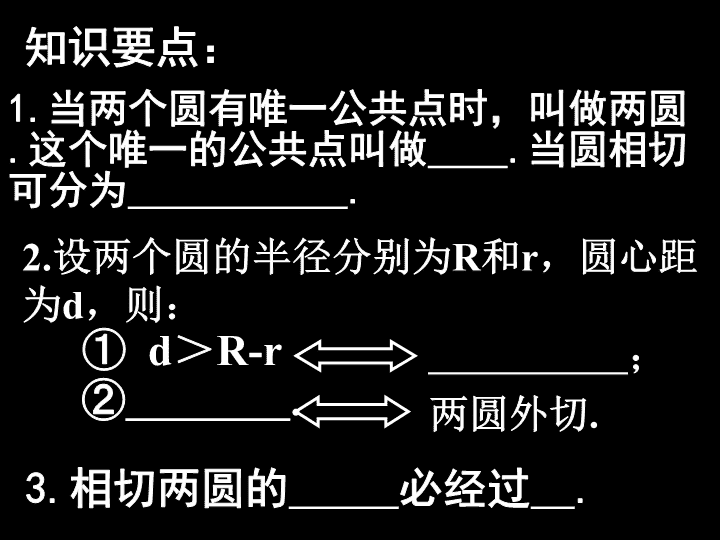
复习六 两圆相切 复习目标: 1. 了解两圆相切、外切、内切的概念 ; 理解相切两圆的性质 . 2. 会判断两圆外切或内切 , 会用两圆相切的判定、性质进行计算或证明 . 3. 会用相切两圆的知识解相关的综合性问题 . 复习指导: 回忆下列知识点 , 会的直接写 , 不会的可翻书查找 , 边填边记 ,5 分钟后 , 比谁能正确填写 , 并能运用它们解题 . 知识要点: 1. 当两个圆有唯一公共点时,叫做两圆 . 这个唯一的公共点叫做 . 当圆相切可分为 . 2. 设两个圆的半径分别为 R 和 r ,圆心距为 d ,则: ② . 两圆外切 . ① d > R-r ; 3. 相切两圆的 必经过 . 检测练习: 1. 已知两圆相切 , 半径分别为 4 和 9, 那么两圆的圆心距为 . 2. 已知 ⊙O 1 与 ⊙O 2 , 连结 O 1 、 O 2 . 若 O 1 O 2 =6, ⊙O 2 的半径为 11, 则 ⊙O 1 的半径为 . 3. 若 ⊙O 1 、 ⊙O 2 、 ⊙O 3 两两外切 , 且半径分别为 2cm 、 3cm 和 10cm ,则 △O 1 O 2 O 3 的形状是 . 4. 已知两个半径为 1 的圆相外切,半径为 2 且和这两个圆都相切的圆共有 个 . A B C D O 1 O 2 5. 如图 , 已知正方形 ABCD 的边长为 4cm, 两个等圆 ⊙O 1 、 ⊙O 2 外切 , ⊙O1 与 AB 、 AD 相切 ,⊙O2 与 BC 、 DC 相切 , 则这两个的半径为 . B A C D O 1 O 2 6. 如图 ,⊙O1 与 ⊙O2 外切于 A,AB 是 ⊙O1 的直径 ,BD 切 ⊙O2 于 D, 交 ⊙O1 于 C, 连结 AC 、 AD. 求证 : AB AC CD BD = 7. 如图 ,⊙O 1 与 ⊙O 2 外切于 P, 过 P 的直线分别交两圆于 B,A,⊙O 1 的切线交 ⊙O 2 于 M,N,AC 为 ⊙O 2 的弦 , 设弦 AC 交 BN 于 D. ⑴ 求证 :PA·AB=AC·AD. B A C D O 1 O 2 M N ⑵ 当弦 AC 绕 A 点旋转 , 弦 AC 的延长线交直线 BN 于 D 点时 , 试问 ⑴ 的结论是否成立 ? 试证明 . A C D P B O 8.如图⊙ O 和⊙ B 外切于 A 点,两圆的外公切线 CD 交 OB 的延长线于点 P,C、D 为切点.连结 OC,BD, 设 R,r 分别为⊙ O, ⊙ B 的 半径( R>r),Rr =25,AC,AD 是方程 x 2 -2(m+2)x+2m 2 -m+3=0 的两个根( AC>AD). ⑴ 求证:∠ CAD=90 0 ⑵求 m 的值; ⑶求 PO 的长. 课堂作业: 1.已知两圆半径是方程 x 2 -12x+6=0 的两根,且圆心距为12,则两圆的位置关系是 . 2.两圆相切,公切线共有 条. 3.若半径分别为4 cm 和2 cm 的两圆外切,则外公切线长是 . B A C D E O 1 O 2 4.两圆内切于 A, 大圆的弦 BC 交小圆于 D,E. ⑴ 求证:∠ BAD=∠EAC . ⑵若 大圆的弦 BC 与小圆相切于 P( 即 D 与 E 重合于 P), 此时类似⑴的结论是否成立?试证明之.查看更多