北京市石景山区2007年初中升学模拟考试

北京市石景山区2007年初中升学模拟考试

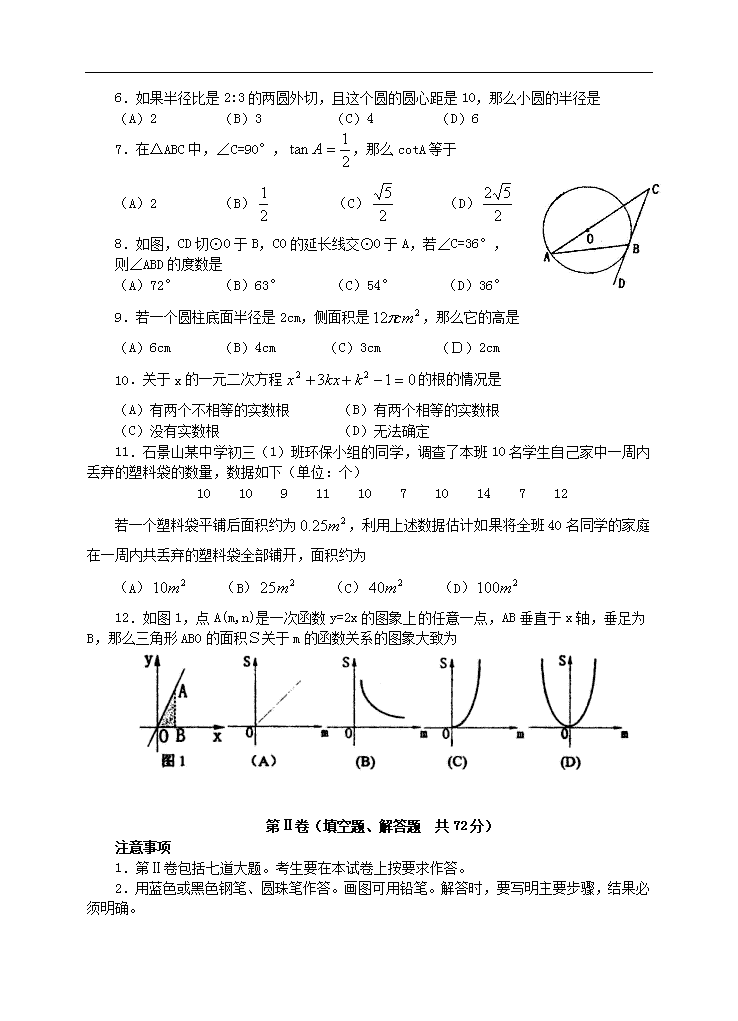
北京市石景山区2007年初中升学模拟考试 数学试卷 ‎2007．5‎ 考生须知 ‎1．本试卷满分为120分，考试时间为120分钟。‎ ‎2．本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（填空题、解答题）两部分，共8页。‎ ‎3．认真填写第1、5页密封线内的学校、姓名、报名号和座位号。‎ 第Ⅰ卷（选择题 48分）‎ 注意事项 ‎1．考生按要求在机读答题卡上作答，题号要对应，填涂要规范。‎ ‎2．考试结束，将试卷和机读答题卡一并交回。‎ 一、选择题（共12小题，每小题4分，共48分）‎ 在每个小题给出的四个备选答案中，只有一个是正确的，请将所选答案前的字母按规定要求涂抹在“机读答题卡”第1-12题的相应位置上。‎ ‎1．的倒数是 ‎（A）3　　　　 （B）-3　　　　 （C）　　　　 （D）‎ ‎2．计算的结果是 ‎（A）0　　　　 （B）1　　　　　（C）2004-π　　 （D）π-2004‎ ‎3．下列运算正确的是 ‎（A）　　　　　　　 （B）‎ ‎（C）　　　　　　　　（D）‎ ‎4．据国家统计局发布的《2003年国民经济和社会发展统计公报》显示，2003年我国国内生产总值约为116700亿元，这个国内生产总值用科学记数法可表示为 ‎（A）　　　　　 （B）‎ ‎（C）　　　　　 （D）‎ ‎5．在函数中，自变量x的取值范围是 ‎（A）x≥3　　　（B）x≠3　　　 （C）x>3　　　 （D）x<3‎ ‎6．如果半径比是2:3的两圆外切，且这个圆的圆心距是10，那么小圆的半径是 ‎（A）2　　　　 （B）3　　　　　（C）4　　　　 （D）6‎ ‎7．在△ABC中，∠C=90°，，那么cotA等于 ‎（A）2　　　　 （B）　　　　 （C）　　　 （D）‎ ‎8．如图，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，‎ 则∠ABD的度数是 ‎（A）72°　　　（B）63°　　　 （C）54°　　　 （D）36°‎ ‎9．若一个圆柱底面半径是‎2cm，侧面积是，那么它的高是 ‎（A）‎6cm　　　 （B）‎4cm　　　 （C）‎3cm　　　　（Ｄ）‎‎2cm ‎10．关于x的一元二次方程的根的情况是 ‎（A）有两个不相等的实数根　　　 （B）有两个相等的实数根 ‎（C）没有实数根　　　　　　　　 （D）无法确定 ‎11．石景山某中学初三（1）班环保小组的同学，调查了本班10名学生自己家中一周内丢弃的塑料袋的数量，数据如下（单位：个）‎ ‎10　　10　　9　　11　　10　　7　　10　　14　　7　　12‎ 若一个塑料袋平铺后面积约为，利用上述数据估计如果将全班40名同学的家庭在一周内共丢弃的塑料袋全部铺开，面积约为 ‎（A）　　 （B）　　 （C）　　 （D）‎ ‎12．如图1，点A(m,n)是一次函数y=2x的图象上的任意一点，AB垂直于x轴，垂足为B，那么三角形ABO的面积Ｓ关于m的函数关系的图象大致为 第Ⅱ卷（填空题、解答题　共72分）‎ 注意事项 ‎1．第Ⅱ卷包括七道大题。考生要在本试卷上按要求作答。‎ ‎2．用蓝色或黑色钢笔、圆珠笔作答。画图可用铅笔。解答时，要写明主要步骤，结果必须明确。‎ 二、填空题（本题共16分，每小题4分）‎ ‎13．不等式3x+2>5x-3的正整数解是_____________。‎ ‎14．在你学过的几何图形中，是轴对称图形的有______________（写出两个即可）。‎ ‎15．如图，四边形ABCD是⊙O的内接矩形，AB=2，BC=4，‎ E是BC的中点，AE的延长线交⊙O于点F，则EF的长 是_________。‎ ‎16．观察下表中三角形个数变化规律，填表并回答下面问题。‎ 问题：如果图中三角形的个数是102个，则图中应有___________条横截线。‎ 三、（共4个小题，共19分）‎ ‎17．（本小题满分4分）‎ 分解因式：‎ 解：‎ ‎18．（本小题满分4分）‎ 计算：‎ 解：‎ ‎19．（本小题满分5分）‎ 用换元法解方程：‎ 解：‎ ‎20．（本小题满分6分）‎ 如图，为了测量河对岸某建筑物AB的高度，在平地上点C处测得建筑物顶端A的仰角为30°，沿CB方向前进‎12米到达D处，在D处测得建筑物顶端A的仰角为45°，求建筑物AB的高度（结果保留根号）。‎ 四、（本题6分）‎ ‎21．请看下面小明同学完成的一道证明题的思路：‎ ‎【证明题】如图1，已知△ABC中，AB=AC，CD⊥AB，垂足是D，P是BC边上任意一点，PE⊥AB，PF⊥AC，垂足分别是E、F 求证：PE+PF=CD 证明思路：‎ 如图2，过点P作PG⊥AB交CD于G，‎ 则四边形PGDE为矩形，PE=GD 又可证△PGC≌△CFP，则PF=CG 所以PE+PF=DG+GC=DC ‎【问题】若P是BC延长线上任意一点，其它条件不变，则PE、PF与CD有何关系？请你写出结论并完成证明过程。‎ 结论：‎ 证明：‎ 五、（本题6分）‎ ‎22． 列方程或方程组解应用题：‎ 某商场销售某种商品，第一个月将此商品的进价加价20%作为销售价，共获利6000元，第二个月商场搞促销活动，将商品的进价加价10%作为销售价，第二个月的销售量比第一个增加了100件，并且商场第二个月比第一个月多获利2000元，问此商品进价是多少元？商场第二个月共销售多少件？‎ 解：‎ 六、（本题8分）‎ ‎23．已知：等边△ABC中，AB、cosB是关于x的方程的两个实数根。若D、E分别是BC、AC上的点，且∠ADE=60°，设BD=x，AE=y，求y关于x的函数关系式，并求出y的最小值。‎ 解：‎ 七、（本题8分）‎ ‎24．已知：如图：BC是半圆O的直径，D、E是半圆O上两点，，CE的延长线与BD的延长线交于点A，过点E作EF⊥BC于点F，交CD与点G。‎ ‎（1）求证：AE=DE ‎（2）若，,求DG；‎ 解：‎ 八、（本题9分）‎ ‎25．已知抛物线 ‎（1）证明抛物线顶点一定在直线y=-x+3上；‎ ‎（2）若抛物线与x轴交于M、N两点，当OM·ON=3，且OM≠ON时，求抛物线的解析式；‎ ‎（3）若（2）中所求抛物线顶点为C，与y轴交点在原点上方，抛物线的对称轴与x轴交于点B，直线y=-x+3与x轴交于点A。点P为抛物线对称轴上一动点，过点P作PD⊥AC，垂足D在线段AC上。试问：是否存在点P，使？若存在，求出点P的坐标；若不存在，请说明理由。‎ 解：‎ 参考答案 一、选择题（每小题4分，共48分）‎ ‎1．B　2．B　3．D　4．A　 5．C　 6．C ‎7．A　8．B　9．C　10．A　11．D　12．D 二、填空题（每小题4分，共16分）‎ ‎13．1，2；‎ ‎14．等腰三角形，矩形，菱形等；‎ ‎15．；‎ ‎16．12……1分；18……1分；16……2分 三、（共4个小题，共19分）‎ ‎17．解：‎ ‎……………………………………2分 ‎=(x-a+1)(x-a-1)……………………………………4分 ‎18．解：‎ ‎……………………………………3分 ‎=2…………………………………………………………4分 ‎19．解：设 则原方程化为：‎ 解得：y=3，y=-1……………………………………………2分 当时，解得：……………………………3分 当时，解得：………………………………4分 经检验：‎ 都是原方程的解………………………………5分 ‎∴原方程的解是 ‎20．解：设AB=x，‎ 在Rt△ACB和Rt△ADB中，‎ ‎∵∠C=30°，∠ADB=45°，CD=12‎ ‎∴DB=x，…………………………………………3分 ‎…………………………………………………5分 ‎∴…………………………………………………6分 答：建筑物AB的高度是米。‎ 四、（本题6分）‎ ‎21．结论：PE-PF=CD…………………………………………2分 证明：证法一 过点C作CG⊥AB于G，‎ ‎∵PE⊥AB，CD⊥AB ‎∴∠CDE=∠DEG=∠EGC=90°‎ ‎∴四边形CGED为矩形，……………………………………3分 CD=GE，GC//AB ‎∴∠GCP=∠B 又AB=AC ‎∴∠B=∠ACB ‎∴∠FCP=∠ACB=∠B=∠GCP 在△PFC和△PGC中，‎ ‎∴△PFC≌△PGC………………………………………………5分 ‎∴PF=PG ‎∴PE-PF=PE-PG=GE=CD………………………………………6分 证法二：‎ 过点P作PG⊥AB于DC延长线于G仿证法一证明步骤酌情给分。‎ 五、（本小题满分6分）‎ ‎22．解：设此商品进价是x元………………………………1分 则………………………………3分 解得：x=500……………………………………………………4分 经检验：x=500是方程的根……………………………………5分 答：此商品进价是500元，商场第二个月共销售160件………………6分 六、（本小题满分8分）‎ ‎23．（1）∵△ABC是等边三角形 ‎∴‎ ‎∴……………………………………2分 解得：‎ ‎∵‎ ‎∵m=0不合题意，舍去 ‎∴m=2即AB=8……………………………………………4分 ‎（2）∵∠ADE=60°‎ ‎∴∠ADB+∠CDE=120°‎ 又∠ADB+∠BAD=180°-∠B=120°‎ ‎∴∠BAD=∠CDE 又∵∠B=∠C=60°‎ ‎∴△ABD∽△DCE……………………………………6分 ‎∴‎ 设BD=x，EA=y则DC=8-x，CE=8-y ‎∴‎ ‎∴‎ ‎∴当BD=4，即D为BC的中点时，EA有最小值6。……………………8分 七、（本小题满分8分）‎ ‎24．‎ ‎（1）证明：∵BC是半圆O直径 ‎∴∠ADC=∠BDC=90°‎ ‎∵‎ ‎∴∠EDC=∠ECD ‎∴∠A=∠ADE ‎∴AE=DE……………………………………………………3分 ‎（2）连结BE ‎∵‎ ‎∴DE=EC ‎∴‎ ‎∵BC是半圆O直径 ‎∴∠BEC=90°即BE⊥AC ‎∴BA=BC ‎∵Rt△BDC中，‎ 设BD=3x，CD=4x，则BC=5x ‎∴AB=BC=5x，AD=2x ‎∵AE·AC=AD·AB ‎∴‎ 解得：x=2，即CD=8……………………………………6分 ‎∵EF⊥BC ‎∴∠CEF+∠ECB=90°‎ ‎∵B，C，E，D四点共圆 ‎∴∠ADE=∠ECB 又∵∠EDC+∠ADE=90°‎ ‎∴∠CEF=∠EDC ‎∵∠DCE为公共角 ‎∴△ECG∽△DCE ‎∴‎ ‎∴……………………………………8分 注：其它解法酌情给分。‎ 八、（本小题满分9分）‎ ‎25．解：‎ ‎（1）‎ ‎∴顶点坐标为（m,-m+3）‎ ‎∴顶点在直线y=-x+3上………………………………2分 ‎（2）∵抛物线与x轴交于M、N两点 ‎∴△>0‎ 即：‎ 解得：m<3……………………………………3分 ‎∵OM·ON=3‎ ‎∴‎ 当时，‎ ‎，‎ ‎∴m=0，m=-1‎ ‎∴当m=0时，‎ ‎（与OM≠ON矛盾，舍）‎ ‎∴m=-1‎ 当时，‎ ‎，‎ ‎∴m=2，m=-3‎ ‎∴‎ ‎……………………………………6分 ‎（3）∵抛物线与y轴交点在原点的上方 ‎∴，‎ ‎∴C（-1，4），B（-1，0）‎ ‎∵直线y=-x+3与x轴交于点A ‎∴A（3，0）‎ ‎∵BA=BC ‎∴∠PCD=45°‎ ‎∴设PD=DC=x，‎ 则，‎ ‎∵‎ ‎∴‎ 解得：‎ 当时，‎ ‎∴‎ ‎∴‎ ‎∴‎ 当时，‎ ‎∴‎ ‎∴‎ ‎∴或………………………………9分