- 2021-11-11 发布 |
- 37.5 KB |
- 20页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版数学九年级上册课件-第24章- 复习课
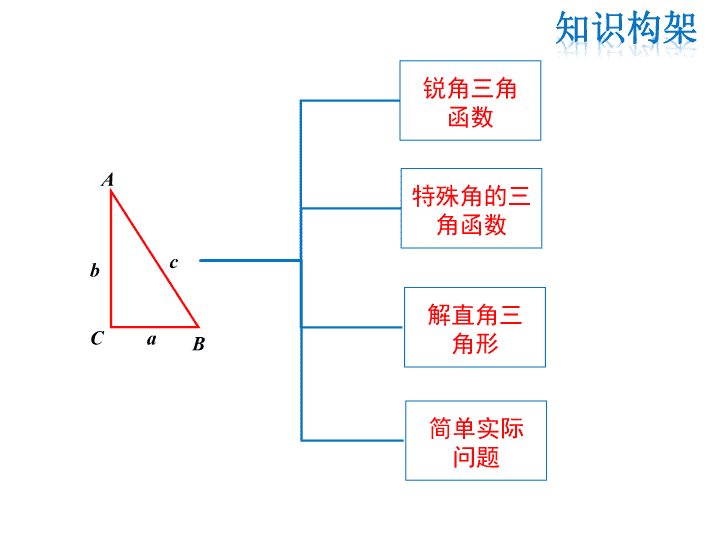
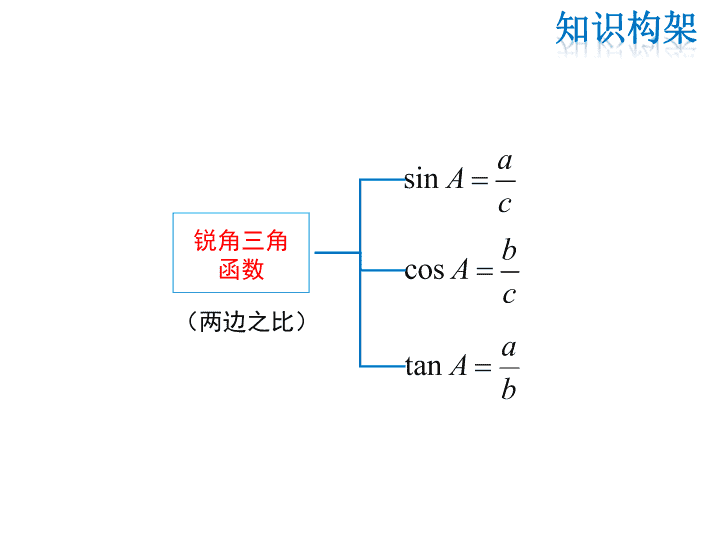
第24章 解直角三角形 复习课 锐角三角 函数 特殊角的三 角函数 解直角三 角形 简单实际 问题 c a b A BC 锐角三角 函数 sin aA c cos bA c b aA tan (两边之比) 特殊角的三 角函数 2 130sin 2 330cos 3 330tan 2 245sin 2 245cos 145tan 2 360sin 2 160cos 360tan 3 2 1 30° 21 1 45° 3 2 1 60° 解直角 三角形 ∠A+ ∠ B=90° a2+b2=c2 三角函数 关系式 计算器 由锐角求三角函数值 由三角函数值求锐角 AbBcAca tancossin A aBcAcb tan sincos B b A b B a A ac sincoscossin 简单实 际问题 数学模型 解直角三角形 梯形 组合图形 三角形 构建 作高转 化为直 角三角 形 (2)∠A的余弦:cosA= = ; (3)∠A的正切:tanA= = . ∠A的邻边 斜边 b c ∠A的对边 ∠A的邻边 a b 易错点: 忽视用边的比表示锐角的正弦、余弦和正切的 前提是在直角三角形中. 2.30°、45°、60°角的三角函数值 sin30°= ,sin45°= ,sin60°= ; cos30°= ,cos45°= ,cos60°= ; tan30°= ,tan45°= ,tan60°= . 3.解直角三角形的依据 (1)在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、 ∠C的对边. 1 2 2 2 3 2 3 2 2 2 1 2 3 3 1 3 三边关系: ; 三角关系: ; 边角关系:sinA=cosB= ,cosA=sinB= , tanA= ,tanB= . (2)直角三角形可解的条件和解法 条件:解直角三角形时知道其中的2个元素(至少有一个是 边),就可以求出其余的3个未知元素. a2+b2=c2 ∠A=90°-∠B a c sinA cosA sinB cosB 解法:①一边一锐角,先由锐角关系求出另一锐角;知 斜边,再用正弦(或余弦)求另两边;知直角边用正切求另一 直角边,再用正弦或勾股定理求斜边.②知两边:先用勾股 定理求另一边,再用边角关系求锐角.③斜三角形问题可通 过添加适当的辅助线转化为解直角三角形问题. 1.如图,在△ABC中,∠C=90°,点D在BC上,BD=4,AD =BC,cos∠ADC= ,求:(1)DC的长;(2)sinB的值. 5 3 分析:题中给出了两个直角三角形,DC和sinB可分别在 Rt△ACD和Rt△ ABC中求得,由AD=BC,图中CD=BC-BD, 由此可列方程求出CD. A B CD 解:(1)设CD=x,在Rt△ACD中,cos∠ADC= , xAD AD x 3 5, 5 3 , 3 5, xBCBCAD 又BC-CD=BD, 4 3 5 xx 解得x=6. ∴CD=6. A B CD 5 3 . , (2) BC=BD+CD=4+6=10=AD. 在Rt△ACD中, 8610 2222 CDADAC 在Rt△ABC中, 4121006422 BCACAB 41 414 412 8sin AB ACB . , . 解析: 要求△ABC的周长,先通过解Rt△ADC求出CD 和AD的长,然后根据勾股定理求出AB的长. 解:在 Rt△ADC 中, ∵sin∠ADC= AC AD, ∴AD= AC sin∠ADC= 3 sin60°=2. ∴BD=2AD=4. ∵tan∠ADC= AC DC, ∴DC= AC tan∠ADC= 3 tan60°=1. ∴BC=BD+DC=5. 在 Rt△ABC 中,AB= AC2+BC2=2 7. ∴△ABC 的周长=AB+BC+AC=2 7+5+ 3. 3.如图所示,电视塔高AB为610米,远处有一栋大楼, 某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔 顶B的仰角为39°. (1)求大楼与电视塔之间的距离AC; (2)求大楼的高度CD(精确到1米). 解析: (1)利用△ABC是等腰直角三角形易得AC的长; (2)在Rt△BDE中,运用直角三角形的边角关系即可求出 BE的长,用AB的长减去BE的长度即可. 解:(1)由题意,得∠ACB=45°,∠A=90°, ∴△ABC是等腰直角三角形, ∴AC=AB=610(米). (2)DE=AC=610.在Rt△BDE中, tan∠BDE= , ∴BE=DE·tan 39°. ∵CD=AE, ∴CD=AB-DE·tan 39°=610- 610×tan39°≈116(米). 即大楼的高度CD约为116米. tan A aA A b 的对边 的邻边 sin A aA c 的对边 斜边 cos A bA c 的邻边 斜边 sin B bB c 的对边 斜边 cos B aB c 的邻边 斜边 tan B bB B a 的对边 的邻边 A B Cb ac 解应用题时,先要将实际问题转化为数学问题,找出直 角三角形并寻找联系已知条件和未知量的桥梁,从而利用解 直角三角形的知识得到数学问题的答案,最后得到符合实际 情况的答案. 解直角三角形的一般思路是:有斜(斜边)用弦(正弦、余 弦),无斜用切(正切),宁乘勿除,取原避中.对于较复杂的 图形,要善于将其分解成简单的图形,并借助桥梁(相等的边、 公共边、相等的角等)的作用将两个图形有机地联系在一起, 从而达到解题的目的.查看更多