北师版九年级数学下册-单元清-第一章检测试卷

北师版九年级数学下册-单元清-第一章检测试卷

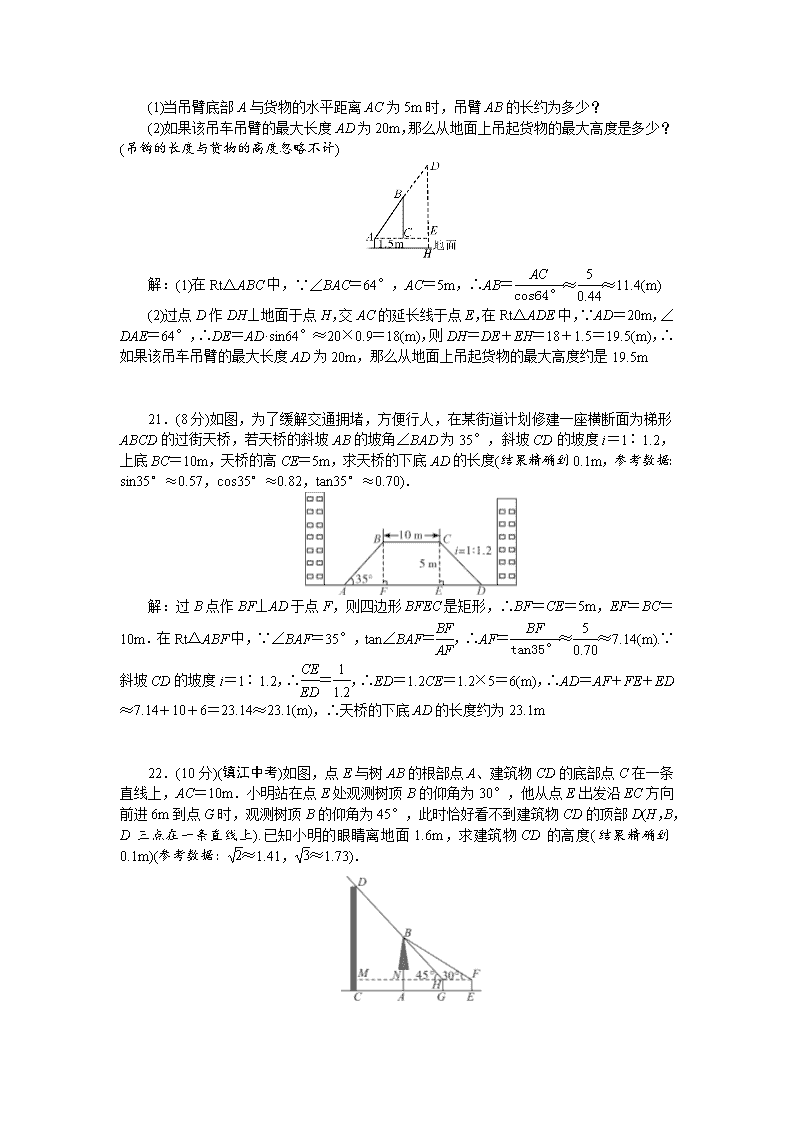
检测内容：第一章 得分________卷后分________评价________ 一、选择题(每小题 3 分，共 30 分) 1．计算 2cos60°的值为(A) A．1B． 3C． 2D．1 2 2．如图，在 8×4 的矩形网格中，每格小正方形的边长都是 1，若△ABC 的三个顶点 在图中相应的格点上，则 tan∠ACB 的值为(A) A．1 3B．1 2C． 2 2 D．3 第 2 题图 第 3 题图 第 4 题图 第 5 题图 3．如图，某地修建高速公路，要从 B 地向 C 地修一条隧道，为测量 B，C 两地间的距 离，某工程师乘热气球从 C 地出发，垂直上升 100m 到达 A 处．在 A 处观察 B 地的俯角为 30°，则 B，C 两地之间的距离为(A) A.100 3mB．50 2mC．50 3mD．100 3 3m 4．如图，点 P 在第二象限，OP 与 x 轴负半轴的夹角是α，且 OP＝10，tanα＝4 3 ，则点 P 的坐标是(B) A．(6，8) B．(－6，8) C．(－8，6) D．(－6，10) 5．如图，在△ABC 中，∠A＝30°，tanB＝ 3 2 ，AC＝2 3，则 AB 的长是(C) A．4B．3＋ 3C．5D．2＋2 3 6．某简易房示意图如图所示，它是一个轴对称图形，则坡屋顶上弦杆 AB 的长为(B) A． 9 5sinαmB． 9 5cosαmC． 5 9sinαmD． 5 9cosαm 第 6 题图 第 7 题图 第 8 题图 第 9 题图 7．如图，在距离铁轨 200m 的 B 处，观察由沈阳开往大连的“和谐号”动车，当动车 车头在 A 处时，恰好位于 B 处的北偏东 60°方向上；10 秒钟后，动车车头到达 C 处，恰好 位于 B 处的西北方向上，则这时段动车的平均速度是(A) A．20( 3＋1) m/sB．20( 3－1) m/sC．200m/sD．300m/s 8．小菁同学在数学实践活动课中测量路灯的高度．如图，已知她的目高 AB 为 1.5m， 她先站在 A 处看路灯顶端 O 的仰角为 35°，再往前走 3m 站在 C 处，看路灯顶端 O 的仰角 为 65°，则路灯顶端 O 到地面的距离约为(已知 sin35°≈0.6，cos35°≈0.8，tan35°≈0.7， sin65°≈0.9，cos65°≈0.4，tan65°≈2.1)(C) A．3.2mB．3.9mC．4.7mD．5.4m 9．(重庆中考)如图，在距某居民楼 AB 楼底 B 点左侧水平距离 60m 的 C 点处有一个山 坡，山坡 CD 的坡度(或坡比)i＝1∶0.75，山坡坡底 C 点到坡顶 D 点的距离 CD＝45m，在坡 顶 D 点处测得居民楼楼顶 A 点的仰角为 28°，居民楼 AB 与山坡 CD 的剖面在同一平面内， 则居民楼 AB 的高度约为(参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53)(B) A．76.9mB．82.1mC．94.8mD．112.6m 10．如图，在矩形 ABCD 中，点 E 是边 BC 的中点，AE⊥BD，垂足为 F，则 tan∠BDE 的值是(A) A. 2 4 B．1 4C．1 3D． 2 3 第 10 题图 第 12 题图 第 14 题图 第 15 题图 二、填空题(每小题 3 分，共 24 分) 11．在△ABC 中，∠C＝90°，AB＝13，BC＝5，则 tanB＝__12 5 __． 12．如图，在 Rt△ABC 中，CD 是斜边 AB 上的中线，已知 CD＝5，BC＝6，则 tanB 的 值是__4 3__． 13．已知α为锐角，且 cos(90°－α)＝ 2 2 ，则α＝__45°__． 14．如图，人字梯 AB，AC 的长都为 2m，当α＝50°时，人字梯顶端离地面的高度 AD 约是 1.5m.(结果精确到 0.1m，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19) 15．(荆州中考)“健康荆州，你我同行”，市民小张积极响应“全民健身动起来”号召， 坚持在某环形步道上跑步．已知此步道外形近似于如图所示的 Rt△ABC，其中∠C＝90°， AB 与 BC 间另有步道 DE 相连，D 地在 AB 正中位置，E 地与 C 地相距 1km.若 tan∠ABC＝3 4 ， ∠DEB＝45°，小张某天沿 A→C→E→B→D→A 路线跑一圈，则他跑了 24km. 16．如图，航拍无人机从 A 处测得一幢建筑物顶部 B 的仰角为 45°，测得底部 C 的俯 角为 60°，此时航拍无人机与该建筑物的水平距离 AD 为 110m，那么该建筑物的高度 BC 约为__300__m．(结果保留整数， 3≈1.73) 第 16 题图 第 17 题图 第 18 题图 17．如图，一艘轮船自西向东航行，航行到 A 处测得小岛 C 位于北偏东 60°方向上， 继续向东航行 10 海里到达点 B 处，测得小岛 C 在轮船的北偏东 15°方向上，此时轮船与小 岛 C 的距离为__5 2__海里．(结果保留根号) 18．(深圳中考)如图，在四边形 ABCD 中，AC 与 BD 相交于点 O，∠ABC＝∠DAC＝90°， tan∠ACB＝1 2 ，BO OD ＝4 3 ，则S△ABD S△CBD ＝ 3 32 ． 三、解答题(共 66 分) 19．(8 分)在 Rt△ABC 中，∠C＝90°，c＝4，a＝2 3，解这个直角三角形． 解：∵在 Rt△ABC 中，∠C＝90°，c＝4，a＝2 3，∴b＝ c2－a2＝2，∴b＝1 2c，∴∠ B＝30°，∠A＝60° 20．(8 分)如图，吊车在水平地面上吊起货物时，吊绳 BC 与地面保持垂直，吊臂 AB 与 水平线的夹角为 64°，吊臂底部 A 距地面 1.5m．(计算结果精确到 0.1m，参考数据：sin64 °≈0.90，cos64°≈0.44，tan64°≈2.05) (1)当吊臂底部 A 与货物的水平距离 AC 为 5m 时，吊臂 AB 的长约为多少？ (2)如果该吊车吊臂的最大长度 AD 为 20m，那么从地面上吊起货物的最大高度是多少？ (吊钩的长度与货物的高度忽略不计) 解：(1)在 Rt△ABC 中，∵∠BAC＝64°，AC＝5m，∴AB＝ AC cos64° ≈ 5 0.44 ≈11.4(m) (2)过点 D 作 DH⊥地面于点 H，交 AC 的延长线于点 E，在 Rt△ADE 中，∵AD＝20m， ∠DAE＝64°，∴DE＝AD·sin64°≈20×0.9＝18(m)，则 DH＝DE＋EH＝18＋1.5＝19.5(m)， ∴如果该吊车吊臂的最大长度 AD 为 20m，那么从地面上吊起货物的最大高度约是 19.5m 21．(8 分)如图，为了缓解交通拥堵，方便行人，在某街道计划修建一座横断面为梯形 ABCD 的过街天桥，若天桥的斜坡 AB 的坡角∠BAD 为 35°，斜坡 CD 的坡度 i＝1∶1.2， 上底 BC＝10m，天桥的高 CE＝5m，求天桥的下底 AD 的长度(结果精确到 0.1m，参考数据： sin35°≈0.57，cos35°≈0.82，tan35°≈0.70)． 解：过 B 点作 BF⊥AD 于点 F，则四边形 BFEC 是矩形，∴BF＝CE＝5m，EF＝BC＝ 10m．在 Rt△ABF 中，∵∠BAF＝35°，tan∠BAF＝BF AF ，∴AF＝ BF tan35° ≈ 5 0.70 ≈7.14(m). ∵斜坡 CD 的坡度 i＝1∶1.2，∴CE ED ＝ 1 1.2 ，∴ED＝1.2CE＝1.2×5＝6(m)，∴AD＝AF＋FE ＋ED≈7.14＋10＋6＝23.14≈23.1(m)，∴天桥的下底 AD 的长度约为 23.1m 22．(10 分)(镇江中考)如图，点 E 与树 AB 的根部点 A、建筑物 CD 的底部点 C 在一条 直线上，AC＝10m．小明站在点 E 处观测树顶 B 的仰角为 30°，他从点 E 出发沿 EC 方向 前进 6m 到点 G 时，观测树顶 B 的仰角为 45°，此时恰好看不到建筑物 CD 的顶部 D(H，B， D 三点在一条直线上).已知小明的眼睛离地面 1.6m，求建筑物 CD 的高度(结果精确到 0.1m)(参考数据： 2≈1.41， 3≈1.73)． 解：延长 FH 交 CD 于点 M，交 AB 于点 N，则 BN＝NH.设 BN＝NH＝xm，在 Rt△BFN 中，∵HF＝6m，∠BFN＝30°，∴tan∠BFN＝BN NF ＝ BN NH＋HF ，即 tan30°＝ x x＋6 ，∴x＝3 3 ＋3，∴NH＝(3 3＋3) m，∴DM＝MH＝MN＋NH＝AC＋NH＝10＋3 3＋3＝(3 3＋13) m， ∴CD＝DM＋MC＝DM＋EF＝(3 3＋13)＋1.6≈19.8(m)，∴建筑物 CD 的高度约为 19.8m 23．(10 分)如图，某大楼的顶部竖有一块广告牌 CD，小明与同学们在山坡的坡脚 A 处 测得广告牌底部D的仰角为53°，沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°， 已知山坡 AB 的坡度 1∶ 3，AB＝10m，AE＝21m(测角器的高度忽略不计，参考数据：tan53° ≈4 3 ，cos53°≈0.60)． (1)求点 B 到地面 AE 的高度； (2)求广告牌 CD 的高度． 解：(1)过点 B 分别作 BG⊥DE 于点 G，BH⊥AE 于点 H，在 Rt△ABH 中，∵i＝tan∠ BAH＝ 1 3 ，∴∠BAH＝30°，∴BH＝1 2AB＝5m，∴点 B 到地面 AE 的高度为 5m (2)易得 AH＝5 3m，∴BG＝HE＝AH＋AE＝(5 3＋21) m．在 Rt△BGC 中，∵∠CBG ＝45°，∴CG＝BG＝(5 3＋21) m．在 Rt△ADE 中，∵∠DAE＝53°，AE＝21m，∴DE＝ AEtan∠DAE≈21×4 3 ＝28(m)，∴CD＝CG＋GE－DE＝5 3＋21＋5－28＝(5 3－2)m，∴广 告牌 CD 的高为(5 3－2)m 24．(10 分)如图，海上观察哨所 B 位于观察哨所 A 的正北方向，距离为 25 海里．在某 时刻，哨所 A 与哨所 B 同时发现一走私船，其位置 C 位于哨所 A 北偏东 53°的方向上，位 于哨所 B 南偏东 37°的方向上． (1)求观察哨所 A 与走私船所在的位置 C 的距离； (2)若观察哨所 A 发现走私船从 C 处以 16 海里/小时的速度向正东方向逃窜，并立即派 缉私艇沿北偏东 76°的方向前去拦截，求缉私艇的速度为多少时，恰好在 D 处成功拦截．(结 果保留根号)(参考数据：sin37°＝cos53°≈3 5 ，cos37°＝sin53°≈4 5 ，tan37°≈3 4 ，tan76° ≈4) 解：(1)∵在△ABC 中，∠ACB＝180°－∠B－∠BAC＝180°－37°－53°＝90°， ∴在 Rt△ABC 中，sinB＝AC AB ，∴AC＝AB·sin37°≈25×3 5＝15(海里).故观察哨所 A 与走私 船所在的位置 C 的距离约为 15 海里 (2)过点 C 作 CM⊥AB 于点 M，由题意易知 D，C, M 在一条直线上，在 Rt△AMC 中， CM＝AC·sin∠CAM≈15×4 5＝12(海里)，AM＝AC·cos∠CAM≈15×3 5＝9(海里).在 Rt△AMD 中，tan∠DAM＝DM AM ，∴DM＝AM·tan76°≈9×4＝36(海里)，∴AD＝ AM2＋DM2＝ 92＋362＝9 17(海里)，CD＝DM－CM＝36－12＝24(海里)，∴当缉私艇的速度约为 16×9 17÷24＝6 17(海里/小时)时，恰好在 D 处成功拦截 25．(12 分)某挖掘机的底座高 AB＝0.8m，动臂 BC＝1.2m，CD＝1.5m，BC 与 CD 的固 定夹角∠BCD＝140°.初始位置如图①，斗杆顶点 D 与铲斗顶点 E 所在的直线 DE 垂直于地 面 AM 于点 E，测得∠CDE＝70°(示意图②)．工作时如图③，动臂 BC 会绕点 B 转动，当 点 A，B，C 在同一直线时，斗杆顶点 D 升至最高点(示意图④)． (1)求挖掘机在初始位置时动臂 BC 与 AB 的夹角∠ABC 的度数； (2)问斗杆顶点 D 的最高点比初始位置高了多少？(精确到 0.1m，参考数据：sin50°≈ 0.77，cos50°≈0.64，sin70°≈0.94，cos70°≈0.34， 3≈1.73) 解：(1)过点 C 作 CG⊥AM 于点 G，∵AB⊥AM，DE⊥AM，∴AB∥CG∥DE，∴∠ DCG＝180°－∠CDE＝110°，∴∠BCG＝∠BCD－∠DCG＝30°，∴∠ABC＝180°－ ∠BCG＝150° (2)过点 C 作 CP⊥DE 于点 P，过点 B 作 BQ⊥DE 于点 Q，交 CG 于点 N，如图②，在 Rt△CPD 中，DP＝CD·cosD＝1.5cos70°≈0.51(m)，在 Rt△BCN 中，CN＝BC·cos∠BCG＝ 1.2cos30°≈1.04(m)，∴DE＝DP＋PQ＋QE＝DP＋CN＋AB＝0.51＋1.04＋0.8＝2.35(m).如 图④，过点 D 作 DH⊥AM 于点 H，过点 C 作 CK⊥DH 于点 K，在 Rt△CKD 中，DK＝CDsin ∠DCK＝1.5sin50°≈1.16(m)，∴DH＝DK＋KH＝DK＋AB＋BC＝1.16＋0.8＋1.2＝ 3.16(m).∵3.16－2.35≈0.8(m)，∴斗杆顶点 D 的最高点比初始位置高了约 0.8m