北师大版数学九年级上册同步练习课件-第1章 特殊平行四边形-第1章 2 一节一练矩形的性质与判定

北师大版数学九年级上册同步练习课件-第1章 特殊平行四边形-第1章 2 一节一练矩形的性质与判定

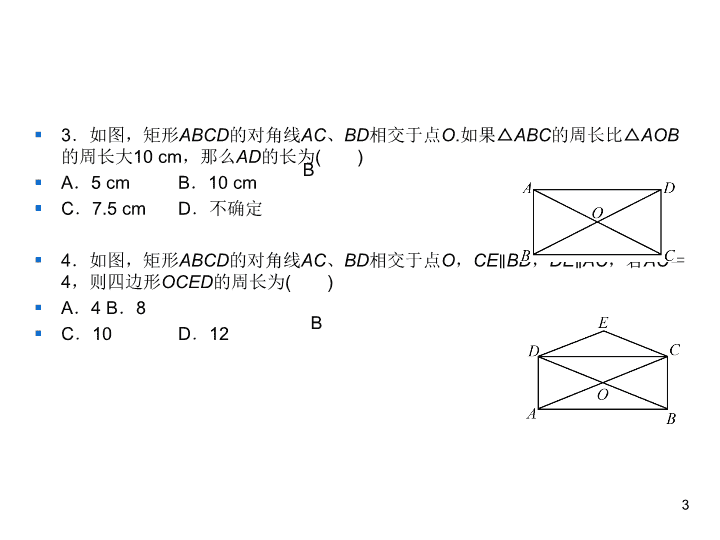
第一章　特殊平行四边形 2　矩形的性质与判定 § 1．【上海中考】已知平行四边形ABCD，AC、BD是它的两条对角线， 那么下列条件中，能判断这个平行四边形为矩形的是(　　) § A．∠BAC＝∠DCA B．∠BAC＝∠DAC § C．∠BAC＝∠ABD D．∠BAC＝∠ADB § 2．如图，在矩形ABCD中，DE⊥AC于点E，∠ADE∶ ∠EDC＝3∶ 2， 则∠BDE的度数为(　　) § A．12° B．18° § C．22° D．36° 2 C 　 B 　 § 3．如图，矩形ABCD的对角线AC、BD相交于点O.如果△ABC的周长比△AOB 的周长大10 cm，那么AD的长为(　　) § A．5 cm B．10 cm § C．7.5 cm D．不确定 § 4．如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若 AC＝4，则四边形OCED的周长为(　　) § A．4 B．8 § C．10 D．12 3 B 　 B 　 § 5．在△ABC中，AB＝3，AC＝4，BC＝5，P为BC上一动点，PE⊥AB 于点E，PF⊥AC于点F，则EF的最小值为(　　) § A．2B．2.2 § C．2.4 D．2.5 § 6．在矩形ABCD中，AB＝1，BC＝2，则BD＝_________. § 7．在矩形ABCD中，对角线AC、BD相交于点O.若∠AOB＝100°，则 ∠OBC＝___________. 4 C 　 50°　 § 8．【2018·湖南株洲中考】如图，矩形ABCD的对角线AC与BD相交于 点O，AC＝10，P、Q分别为AO、AD的中点，则PQ的长度为 ___________. 5 2.5　 9．如图，△ABC中，AC的中垂线交AC、AB于点D、 F，BE⊥DF交DF的延长线于点E，若∠A＝30°，BC＝2， AF＝BF，则四边形BCDE的面积是__________. § 10．如图，已知MN∥PQ，AB、CB分别平分∠MAC、∠PCA，AD、 CD分别平分∠NAC、∠QCA.求证：四边形ABCD是矩形． § 证明：∵MN∥PQ，∴∠MAC＋∠PCA＝180°.∵AB、CB分别平分 ∠MAC、∠PCA，∴∠BCA＋∠BAC＝90°，∴∠B＝90°.同理，∠D ＝90°.∵∠MAC＋∠CAN＝180°，AB、AD分别平分∠MAC、 ∠NAC，∴∠BAD＝90°，∴四边形ABCD是矩形． 6 § 11．如图，四边形ABCD是矩形，△PBC和△QCD都是等边三角形，且 点P在矩形上方，点Q在矩形内．求证： § (1)∠PBA＝∠PCQ＝30°； § (2)PA＝PQ. 7 证明：(1)∵四边形ABCD是矩形，∴∠ABC＝∠BCD＝90°.又∵△PBC是正 三角形，∴∠PBC＝∠PCB＝60°，∴∠PBA＝∠PCD＝30°.又∵△QCD是正三 角形，∴∠QCD＝60°，∴∠PCQ＝∠QCD－∠PCD＝30°，∴∠PBA＝∠PCQ ＝30°.　(2)∵CD＝CQ，CD＝BA，∴BA＝CQ.又∵∠PBA＝∠PCQ＝30°，PB＝ PC，∴△PAB≌△PQC，∴PA＝PQ. § 12．已知矩形ABCD的周长为20 cm，两条对角线AC、BD相交于点O， 过点O作AC的垂线EF，分别交两边AD、BC于点E、F(不与顶点重合)， 则以下关于△CDE与△ABF判断完全正确的一项为(　　) § A．△CDE与△ABF的周长都等于10 cm，但面积不一定相等 § B．△CDE与△ABF全等，且周长都为10 cm § C．△CDE与△ABF全等，且周长都为5 cm § D．△CDE与△ABF全等，但它们的周长和面积都不能确定 8 B 　 § 13．【四川宜宾中考】如图，点P是矩形ABCD的边AD上的一动 点，矩形的两条边AB、BC的长分别是6和8，则点P到矩形的两 条对角线AC和BD的距离之和是 § (　　) § A．4.8 B．5 § C．6 D．7.2 9 A 　 § 14．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD 交于点E、F，连接BF交AC于点M，连接DE、BO.若∠COB＝60°， FO＝FC，则下列结论：①FB垂直平分OC；②△EOB≌ △CMB；③DE ＝EF；④S△AOE∶ S△BCM＝2∶ 3.其中正确的结论有(　　) § A．4个 § B．3个 § C．2个 § D．1个 10 B 　 11 12 D 　 § 16．如图，四边形OABC为矩形，点A、C分别在x轴和y轴上，连接AC， 点B的坐标为(4,3)，∠CAO的平分线与y轴相交于点D，则点D的坐标为 _________. 13 § 17．如图，点P在矩形ABCD的对角线AC上， 且不与点A、C重合，过点P分别作边AB、 AD的平行线，交两组对边于点E、F和G、H. § (1)求证：△PHC≌ △CFP； § (2)证明四边形PEDH和四边形PFBG都是矩 形，并直接写出它们面积之间的关系． 14 15 § 18．如图，在矩形ABCD中，AB＝12，AC＝20，两 条对角线相交于点O.以OB、OC为邻边作第1个平行四 边形OBB1C，对角线相交于点A1；再以A1B1、A1C为 邻边作第2个平行四边形A1B1C1C，对角线相交于点O1； 再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1， 对角线相交于点A2……以此类推． § (1)求矩形ABCD的面积； § (2)求第1个平行四边形OBB1C、第2个平行四边形 A1B1C1C和第6个平行四边形的面积． 16 17