江苏省九年级10月单元测试月考数学试题（苏教版九年级数学上册10月份月考试卷）

江苏省九年级10月单元测试月考数学试题（苏教版九年级数学上册10月份月考试卷）

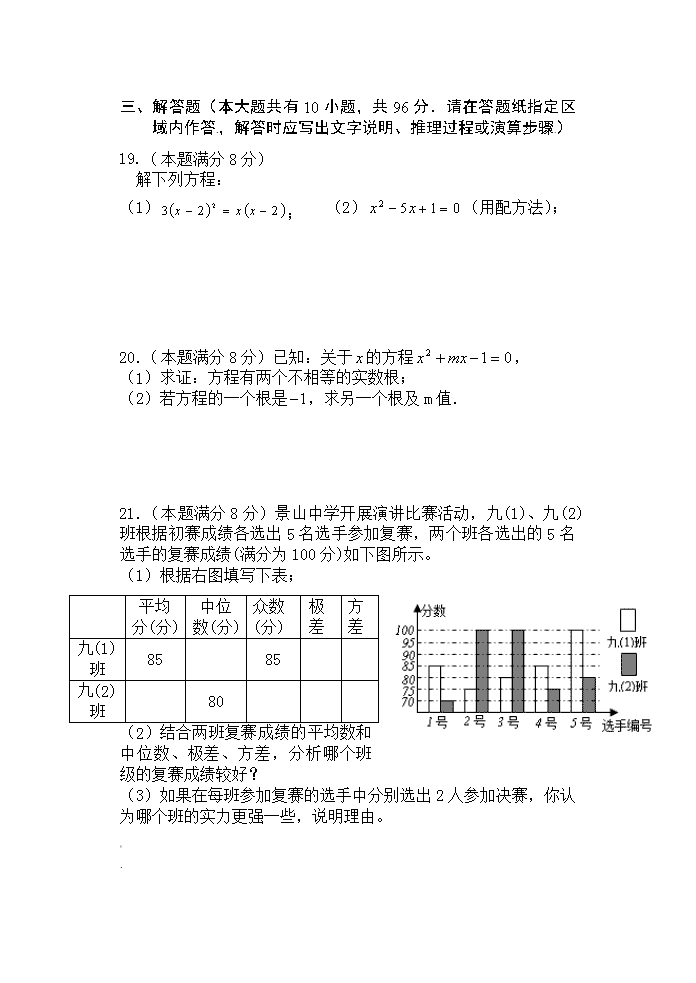
苏教版九年级数学上册 10 月月考测试卷 一．选择题（本大题共有８小题，每小题 3 分，共 24 分．在每小 题所给出的四个选项中，只有一项是符合题目要求的，请将 正确选项的字母代号填涂在答题纸相应位置上） 1.若关于 x 的一元二次方程的两个根为 1 1x  ， 2 2x  ，则这个方程 是 （ ） A. 2 3 2 0x x   B. 2 3 2 0x x   C. 2 2 3 0x x   D. 2 3 2 0x x   2．在统计中，样本的方差可以反映这组数据的 （ ） A．平均状态 B．分布规律 C．离散程度 D．数值大小 3.已知⊙O 的半径是 6cm，点 O 到同一平面内直线 L 的距离为 5cm， 则直线 L 与⊙O 的位置关系是 （ ） A.相交 B.相切 C.相离 D.无法判断 4.如图，在⊙O 中，∠ABC=52°，则∠AOC 等于 （ ） A.52° B.80° C.90° D. 104° 5．甲、乙两人在相同的条件下，各射靶 10 次，经过计算：甲、 乙射击成绩的平均数都是 8 环，甲的方差是 1.2,乙的方差是 1.8．下列说法中不一定正确的是 （ ） A．甲、乙射中的总环数相同 B．甲的成绩稳定 C．乙的成绩波动较大 D．甲、乙的众数相同 6. 以 2、4 为两边长的三角形的第三边长是方程 01072  xx 的 根，则这个三角形的周长为 （ ） A. 8 B.11 C. 11 或 8 D.以上都不对 7.如果关于x的方程 2 2 (2 1) 1 0k x k x    有实数根，那么 k 的取值 范围是 （ ） A. 1 4k   B. k ＞ 1 4  且 0k  C. k ＜ 1 4  D. 1 4k   且 0k  8.在平面直角坐标系 xoy 中，直线经过点 A（－3，0），点 B（0， 3 ），点 P 的坐标为（1，0），⊙P 与 y 轴相切于点 O，若将⊙P 沿 x 轴向左平移，平移后得到（点 P 的对应点为点 P′）⊙P′，当 ⊙P′与直线相交时，横坐标为整数的点 P′共有 （ ） A、4 个 B、3 个 C、2 个 D、1 个 二、填空题（本大题共有 10 小题，每小题 3 分，共 30 分．不需写 出解答过程，请将答案直接写在答题纸相应位置上） 9.方程 042  xx 的解是 （ （ 10.若一元二次方程 0892  xkx 的一个根为 1，则 k= ， 11．数据-5，6，4，0，1，7，5 的极差为 （__ 12．数据 11、12、13、14、15 的方差是 13.请给 C 一个值，C= 时，方程 x2 -3x+C=0 无实数根。 14．如图，△ABC 内接于⊙O，AC 是⊙O 的直径，∠ACB=50°，点 D 是弧 BAC 上一点，则∠D= 度。 15．如图，ABCD 是⊙O 的内接四边形，∠B=140°，则∠AOC 的 度数是 度． 第 14 题 第 15 题 第 17 题 16．已知三角形的三边分别为 13、12、5，则这个三角形的内切圆 半径是 （ （． 17. 如图△ABC 的内接圆于⊙O，∠C=45°，AB=4，则⊙O 的半径为 18. 对于实数 a，b，定义运算“”： 2 2 ( ), ( ). a ab a ba b ab b a b       ＜ 例如 42，因为 4＞2，所以 24 2 4 4 2 8     ．若 1x ， 2x 是一元 二次方程 01272  xx 的两个根，则 1 2x x  ___ . 三、解答题（本大题共有 10 小题，共 96 分．请在答题纸指定区 域内作答，解答时应写出文字说明、推理过程或演算步骤） 19.（本题满分 8 分） 解下列方程： （1）    223 2  xxx ； （2） 0152  xx （用配方法）； 20．（本题满分 8 分）已知：关于 x 的方程 012  mxx ， （1）求证：方程有两个不相等的实数根； （2）若方程的一个根是 1 ，求另一个根及 m 值． 21．（本题满分 8 分）景山中学开展演讲比赛活动，九(1)、九(2) 班根据初赛成绩各选出 5 名选手参加复赛，两个班各选出的 5 名选 手的复赛成绩(满分为 100 分)如下图所示。 （1）根据右图填写下表； （2）结合两班复赛成绩的平均数和中位数、极差、方差，分析哪 个班级的复赛成绩较好？ （3）如果在每班参加复赛的选手中分别选出 2 人参加决赛，你认 为哪个班的实力更强一些，说明理由。 平均 分 (分) 中位 数 (分) 众数 (分) 极 差 方 差 九(1) 班 85 85 九(2) 班 80 22.（本题满分 8 分）如图，AB 与 O⊙ 相切于 C， BA  ， O⊙ 的 半径为 6， OA＝10，求 AB 的长. 23．（本题满分 10 分）如图，在 Rt△ABC 中，∠ACB=90°，以 AC 为直径作⊙O 交 AB 于点 D，连接 CD． （1）求证：∠A=∠BCD； （2）若 M 为线段 BC 上一点，试问当点 M 在什么位置 时，直线 DM 与⊙O 相切？并说明理由． 24．（本题满分 10 分）已知关于 x 的方程 2 ( 2) 2 1 0x m x m     . （1）求证:方程有两个不相等的实数根. (2)是否存在实数 m，使方程的两个实数根互为相反数?若存在， 求出 m 的值；若不存在，说明理由 25．（本题满分 10 分）已知： ABCD 的两边 AB ，AD 的长是关于 x 的方程 04 1 2 2  mmxx 的两个实数根。 （1）当 m 为何值时，四边形 ABCD 是菱形？求出这时菱形的边长； （2）若 AB 的长为 2，那么 ABCD 的周长是多少？ 26．（本题满分 10 分）10 月国庆佳节，景山旅行社为吸引游客组 团去具有喀斯特地貌特征的黄果树风景区旅游，推出了如下收费 标准（如图所示）： 某单位组织员工去具有喀斯特地貌特征的黄果树风景区旅游， 共支付给旅行社旅游费用 27000 元，请问该单位这次共有多少名 员工去具有喀斯特地貌特征的黄果树风景区旅游？ 27.（本题满分 12 分）阅读材料： 已知，如图（1），在面积为 S 的△ABC 中，BC=a，AC=b，AB=c，内切圆O 的半径为 r．连接 OA、OB、OC，△ABC 被划分为三个小三角形． ∵S=S△OBC+S△OAC+S△OAB= BC•r+ AC•r+ AB•r= （a+b+c）r． ∴r= ． （1）类比推理：若面积为 S 的四边形 ABCD 存在内切圆（与各边都相切的 圆），如图（2），各边长分别为 AB=a，BC=b，CD=c，AD=d，求四边形的 内切圆半径 r； （2）理解应用：如图（3），在等腰梯形 ABCD 中，AB∥DC，AB=21，CD=11， AD=13，⊙O1 与⊙O2 分别为△ABD 与△BCD 的内切圆，设它们的半径分别 为 r1 和 r2，求 的值． 28．（本题满分 12 分）如图，已知 L1⊥L2，⊙O 与 L1，L2 都相切， ⊙O 的半径为 1cm，矩形 ABCD 的边 AD、AB 分别与直线 L1，L2 重合， ∠BCA=600，若⊙O 与矩形 ABCD 沿 L1 同时向右移动，⊙O 的移动速 度为 2cm，矩形 ABCD 的移动速度为 3cm/s，设移动时间为t（s） （1）如图①，连接 OA、AC，则∠OAC 的度数为 °； （2）如图②，两个图形移动一段时间后，⊙O 到达⊙O1 的位置， 矩形 ABCD 到达 A1B1C1D1 的位置，此时点 O1，A1，C1 恰好在同一直线 上，求圆心 O 移动的距离（即 OO1 的长）； （3）在移动过程中，求当对角线 AC 所在直线与圆 O 第二次相切 时 t 的值。