- 2021-11-11 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级上册青岛版数学课件3-4直线与圆的位置关系(4)
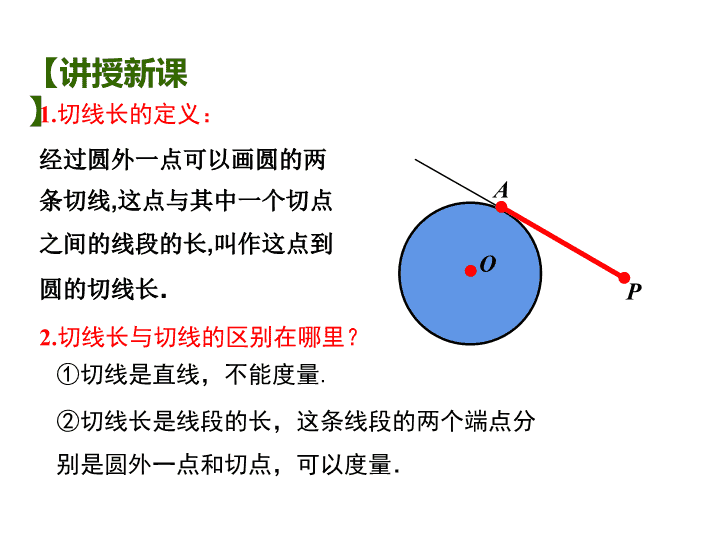
3.4直线与圆的位置关系(4) 同学们玩过空竹和悠悠球吗?在空竹和悠悠球的旋转的那一 瞬间,你能从中抽象出什么样数学图形? 【导入新课】 P 1.切线长的定义: 经过圆外一点可以画圆的两 条切线,这点与其中一个切点 之间的线段的长,叫作这点到 圆的切线长. A O ①切线是直线,不能度量. ②切线长是线段的长,这条线段的两个端点分 别是圆外一点和切点,可以度量. 2.切线长与切线的区别在哪里? 【讲授新课】 思考:PA为☉O的一条切线,沿着直线PO对折,设圆上与点 A重合的点为B. Ø OB是☉O的一条半径吗? Ø PB是☉O的切线吗? (利用图形轴对称性解释) Ø PA、PB有何关系? Ø ∠APO和∠BPO有何关系? O. P A B PO 切线长定理: 过圆外一点所画的圆的两条 切线长相等. PA、PB分别切☉O于A、B PA = PB ∠OPA=∠OPB 几何语言: 切线长定理为证明线段相等、角相等提供了新的方法.注意 O. P A B 已知,如图PA、PB是☉O的两条 切线,A、B为切点. 求证:PA=PB,∠APO=∠BPO. 做一做 证明:∵PA切☉O于点A, ∴ OA⊥PA. 同理可得OB⊥PB. ∵OA=OB,OP=OP, ∴Rt△OAP≌ Rt△OBP, ∴PA=PB,∠APO=∠BPO. 1.PA、PB是☉O的两条切线,A、 B为切点,直线OP交☉O于点D、 E,交AB于C. (1)写出图中所有的垂直关系; OA⊥PA,OB ⊥PB,AB ⊥OP. (3)写出图中所有的全等三角形; △AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP. (4)写出图中所有的等腰三角形.△ABP △AOB (2)写出图中与∠OAC相等的角; ∠OAC=∠OBC=∠APC=∠BPC. P 练一练 P 2.PA、PB是☉O的两条切线,A,B是切点,OA=3. (1)若AP=4,则OP= ; (2)若∠BPA=60 °,则OP= . 5 6 3.如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB 上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E. 已知PA=7,∠P=40°.则 ⑵ ∠DOE= . ⑴ △PDE的周长是 ;14 O P A B C E D 70° 解析:连接OA、OB、OC、OD和OE.∵PA、PB是☉O的 两条切线,点A、B是切点, ∴PA=PB=7.∠PAO=∠PBO=90°. ∠AOB=360°-∠PAO- ∠PBO-∠P=140°. 又∵DC、DA是☉O的两条切线,点C、A是切点,∴DC=DA.同理可得 CE=CB. S△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14. O P A B C E D 1 2 1 2 1 2 ∵OA=OC,OD=OD,∴△AOD≌△COD, ∴∠DOC=∠DOA= ∠AOC. 同理可得∠COE= ∠COB. ∠DOE=∠DOC+∠COE= (∠AOC+ ∠COB)=70°. 切线长问题辅助线添加方法: (1)分别连接圆心和切点; (2)连接两切点; (3)连接圆心和圆外一点. 方法归纳 20 ° 4 如图,PA、PB是☉O的两条切线,切点分别是A、B,如果 AP=4, ∠APB= 40 ° ,则∠APO= ,PB= . P 【练习】 如图,PA、PB是☉O的两条切线,切点为A、B,∠P= 50 °, 点C是☉O上异于A、B的点,则∠ACB= . 65 °或115 ° P 【小结】 切线长 切 线 长 定 理 作 用 图形的轴对称性原 理 提供了证线段和 角相等的新方法 辅助线 ① 分别连接圆心和切点; ② 连接两切点; ③ 连接圆心和圆外一点.查看更多