九年级数学上册第二十二章二次函数22-3二次函数应用2教学课件新版 人教版

九年级数学上册第二十二章二次函数22-3二次函数应用2教学课件新版 人教版

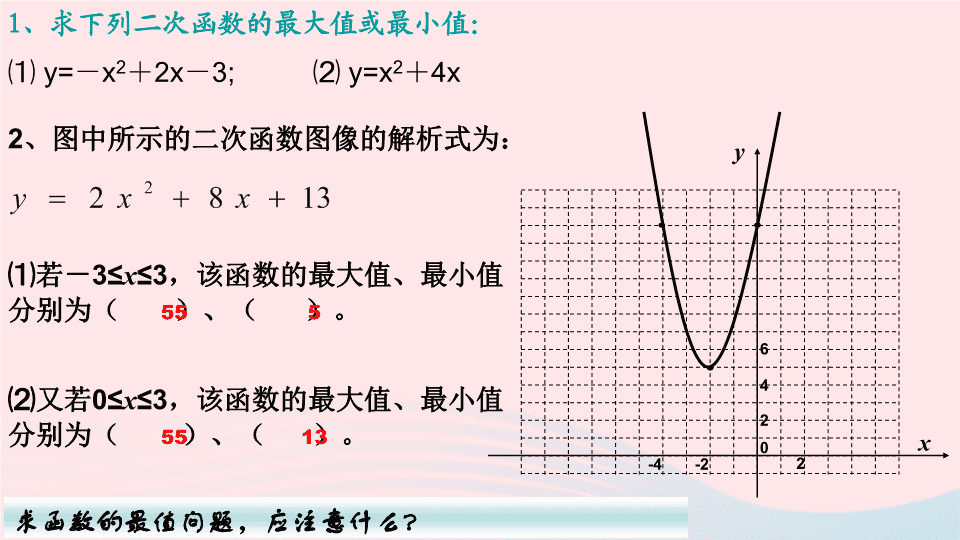
22.3 实际问题与二次函数 (2) 1. 能利用二次函数解决与利润有关的实际问题。 2. 通过对生活中实际问题的探究，体会数学建模思想。 学习目标： -2 0 2 4 6 2 -4 x y ⑴若－ 3≤ x ≤3 ，该函数的最大值、最小值分别为 （ ）、（ ）。 ⑵又若 0≤ x ≤3 ，该函数的最大值、最小值分别为（ ）、（ ）。 求函数的最值问题，应注意什么 ? 55 5 55 13 2 、图中所示的二次函数图像的解析式为： 1 、求下列二次函数的最大值或最小值： ⑴ y= － x 2 ＋ 2x － 3; ⑵ y=x 2 ＋ 4x 某商品现在的售价为每件 60 元，每星期可卖出 300 件，市场调查反映：每涨价 1 元，每星期少卖出 10 件；每降价 1 元，每星期可多卖出 18 件，已知商品的进价为每件 40 元，如何定价才能使利润最大？ 来到商场 请大家带着以下几个问题读题 （ 1 ）题目中有几种调整价格的方法？ （ 2 ）题目涉及到哪些变量？哪一个量是自变量？哪些量随之发生了变化？ 某商品现在的售价为每件 60 元，每星期可卖出 300 件，市场调查反映：每涨价 1 元，每星期少卖出 10 件；每降价 1 元，每星期可多卖出 18 件，已知商品的进价为每件 40 元，如何定价才能使利润最大？ 来到商场 分析 : 调整价格包括涨价和降价两种情况 先来看涨价的情况： ⑴ 设每件涨价 x 元，则每星期售出商品的利润 y 也随之变化，我们先来确定 y 与 x 的函数关系式。涨价 x 元时则每星期少卖 件，实际卖出 件 , 销额为 元，买进商品需付 　　 元 因此，所得利润为 　　　　　　　　　　　　　　　 元 10x (300-10x) (60+x)(300-10x) 40(300-10x) y=(60+x)(300-10x)-40(300-10x) 即 (0≤X≤30) (0≤X≤30) 可以看出，这个函数的图像是一条抛物线的一部分，这条抛物线的顶点是函数图像的最高点，也就是说当 x 取顶点坐标的横坐标时，这个函数有最大值。由公式可以求出顶点的横坐标 . 所以，当定价为 65 元时，利润最大，最大利润为 6250 元 在降价的情况下，最大利润是多少？请你参考 （ 1 ） 的过程得出答案。 解：设降价 x 元时利润最大，则每星期可多卖 18x 件，实际卖出（ 300+18x) 件，销售额为 (60-x)(300+18x) 元，买进商品需付 40(300-10x) 元，因此，得利润 答：定价为 元时，利润最大，最大利润为 6050 元 做一做 由 (1)(2) 的讨论及现在的销售情况 , 你知道应该如何定价能使利润最大了吗 ? (0≤x≤20) 归纳小结 ： 运用二次函数的性质求实际问题的最大值和最小值的一般步骤 : 求出函数解析式和自变量的取值范围 配方变形，或利用公式求它的最大值或最小值。 检查求 得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。 解这类题目的一般步骤 某商场销售某种品牌的纯牛奶，已知进价为每箱 40 元，市场调查发现：若每箱以 50 元销售 , 平均每天可销售 100 箱 . 价格每箱降低 1 元，平均每天多销售 25 箱 ; 价格每箱升高 1 元，平均每天少销售 4 箱。如何定价才能使得利润最大？ 练一练 若生产厂家要求每箱售价在 45—55 元之间。 如何定价才能使得利润最大？（为了便于计算，要求每箱的价格为整数） 有一经销商，按市场价收购了一种活蟹 1000 千克，放养在塘内，此时市场价为每千克 30 元。据测算，此后每千克活蟹的市场价，每天可上升 1 元，但是，放养一天需各种费用支出 400 元，且平均每天还有 10 千克蟹死去，假定死蟹均于当天全部售出，售价都是每千克 20 元（放养期间蟹的重量不变） . ⑴ 设 x 天后每千克活蟹市场价为 P 元，写出 P 关于 x 的函数关系式 . ⑵ 如果放养 x 天将活蟹一次性出售，并记 1000 千克蟹的销售总额为 Q 元，写出 Q 关于 x 的函数关系式。 ⑶该经销商将这批蟹放养多少天后出售，可获最大利润，（利润 = 销售总额 - 收购成本 - 费用）？最大利润是多少？ 思考 解：①由题意知 :P=30+x. ② 由题意知：死蟹的销售额为 200x 元，活蟹的销售额为（ 30+x ）（ 1000-10x) 元。 驶向胜利的彼岸 ∴ Q=(30+x)(1000-10x)+200x=-10x2+900x+30000 ③设总利润为 W=Q-30000-400x=-10x2+500x =-10(x-25)2+6250 ∴ 当 x=25 时，总利润最大，最大利润为 6250 元。 x( 元 ) 15 20 30 … y( 件 ) 25 20 10 … 若日销售量 y 是销售价 x 的一次函数。 （ 1 ）求出日销售量 y （件）与销售价 x （ 元）的函数关系式；（ 6 分） （ 2 ）要使每日的销售利润 最大 ，每件产品的销售价应定为多少元？此时每日销售利润是多少元？（ 6 分） 某产品每件成本 10 元，试销阶段每件产品的销售价 x （元）与产品的日销售量 y （件）之间的关系如下表： 中考题选练 （ 2 ）设每件产品的销售价应定为 x 元，所获销售利润为 w 元。则 产品的销售价应定为 25 元，此时每日获得最大销售利润为 225 元。 则 解得： k= － 1 ， b ＝ 40 。 1 分 5 分 6 分 7 分 10 分 12 分 （ 1 ）设此一次函数解析式为 。 所以一次函数解析为 。 设旅行团人数为 x 人 , 营业额为 y 元 , 则 旅行社何时营业额最大 1. 某旅行社组团去外地旅游 ,30 人起组团 , 每人单价 800 元 . 旅行社对超过 30 人的团给予优惠 , 即旅行团每增加一人 , 每人的单价就降低 10 元 . 你能帮助分析一下 , 当旅行团的人数是多少时 , 旅行社可以获得最大营业额？ 某宾馆有 50 个房间供游客居住，当每个房间的定价为每天 180 元时，房间会全部住满。当每个房间每天的定价每增加 10 元时，就会有一个房间空闲。如果游客居住房间，宾馆需对每个房间每天支出 20 元的各种费用 . 房价定为多少时，宾馆利润最大？ 解：设每个房间每天增加 x 元，宾馆的利润为 y 元 Y=(50-x/10)(180+x)-20(50-x/10) Y=-1/10x2+34x+8000 大显身手 1. 某商场销售一批名牌衬衫，平均每天可售出 20 件，每件盈利 40 元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施。经调查发现，如果每件衬衫每降价 1 元，商场平均每天可多售出 2 件。 （ 1 ）若商场平均每天要盈利 1200 元，每件衬衫应降价多少元？ （ 2 ）每件衬衫降价多少元时，商场平均每天盈利最多？ （三） 销售问题 2. 某商场以每件 42 元的价钱购进一种服装，根据试销得知这种服装每天的销售量 t （件）与每件的销售价 x （元 / 件）可看成是一次函数关系： t ＝－ 3x ＋ 204 。 （ 1 ） . 写出商场卖这种服装每天销售利 y （元）与每件的销售价 x （元）间的函数关系式； （ 2 ） . 通过对所得函数关系式进行配方，指出 商场要想每天获得最大的销售利润，每件的销售价定为多少最为合适？最大利润为多少？ 3. 某个商店的老板，他最近进了价格为 30 元的书包。起初以 40 元每个售出，平均每个月能售出 200 个。后来，根据市场调查发现：这种书包的售价每上涨 1 元，每个月就少卖出 10 个。现在请你帮帮他 . (1). 如何定价才使他的利润最大 ？ (2). 如何定价才使他的利润达到 2160 元 ？