- 2021-11-10 发布 |
- 37.5 KB |
- 28页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级上册青岛版数学课件1-4图形的位似(1)
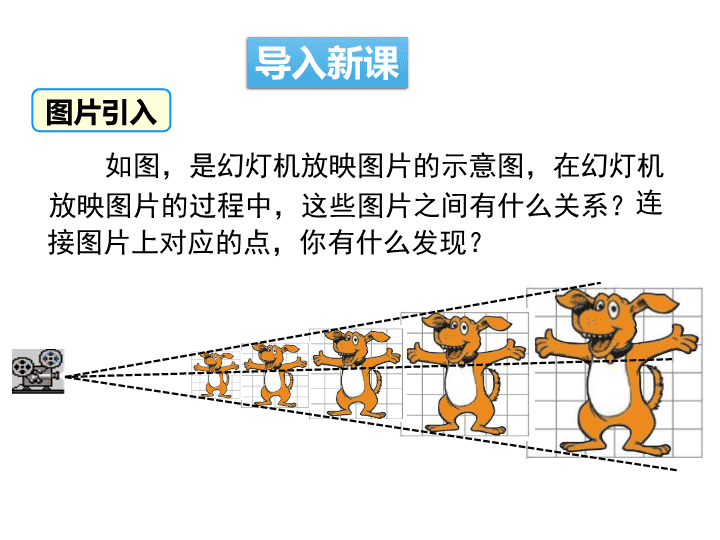
1.4图形的位似(1) 1. 掌握位似图形的概念、性质和画法. (重点) 2. 掌握位似与相似的联系与区别. (难点) 学习目标 如图,是幻灯机放映图片的示意图,在幻灯机 放映图片的过程中,这些图片之间有什么关系? 图片引入 连 接图片上对应的点,你有什么发现? 导入新课 问题1:下列图形中有相似多边形吗?如果有,这种 相似有什么特征? 观察与思考 讲授新课 位似图形的概念知识点1 问题2:下面两个多边形相似,将两个图形的顶点相连, 观察发现连接的直线相交于点O. 有 什么关系? A B C D E E' D' C' B' A' O .OA' OB' OC' OD' OE' OA OB OC OD OE OE OE',OD OD',OC OC',OB OB',OA OA' 对应边互相平行(或共线)且每对对应点所在的直线都 经过同一点的两个相似多边形叫作位似图形,这个点叫 作位似中心.. 概念学习 判断两个图形是不是位似图形,需要从两方面去 考察:一是这两个图形是相似的,二是要有特殊的位 置关系,即每组对应点所在的直线都经过同一点. 1. 画出下列图形的位似中心: 练一练 2. 如图,BC∥ED,下列说法不正确的是 ( ) A. 两个三角形是位似图形 B. 点 A 是两个三角形的位似中心 C. B 与 D,C 与 E是对应位似点 D. AE : AD是相似比 D DE A B C 合作探究 从左图中我们可以看到,△OAB∽△OA′B′, 则 ,AB∥A′B′. 右图呢?你得 到了什么? OA OB AB OA' OB' A' B' A B E C D O A′ B′ C′ D′ E′ A B C O A′ B′ C′ 位似图形的性质知识点2 1. 位似图形是一种特殊的相似图形,它具有相似 图形的所有性质,即对应角相等,对应边的比 相等. 2. 位似图形上任意一对对应点到位似中心的距 离之比等于相似比.(位似图形的相似比也 叫作位似比) 3. 对应线段平行或者在一条直线上. 归纳: 如图,四边形木框 ABCD 在灯泡发出的光照射 下形成的影子是四边形 A′B′C′D′,若 OB : O′B′= 1 : 2,则四边形 ABCD 的面积与四边形A′B′C′D′的面 积比为 ( ) A.4∶ 1 B. ∶ 1 C.1∶ D.1∶ 4 D 2 2 O 练一练 例1:如图,已知△ABC,以点O为位似中心画 △DEF,使其与△ABC位似,且位似比为2. 解:画射线OA,OB,OC;在射线 OA,OB,OC上分别取点D,E,F,使 OD = 2OA,OE = 2OB,OF = 2OC; 顺序连接D,E,F,使△DEF与 △ABC位似,相似比为2. A B C F E D O 想一想:你还有其他的画法吗? 位似多边形的画法知识点3 A B C 画法二:△ABC与△DEF异侧. 解:画射线OA,OB,OC;沿着射线 OA,OB,OC反方向上分别取点D,E,F, OD = 2OA,OE = 2OB,OF = 2OC; 顺序连接D,E,F,使△DEF与△ABC位似, 相似比为2. O E F D (3) 顺次连接点 A' 、B' 、C' 、D' ,所得四边形 A' B' C' D' 就是所要求的图形. O D A B C A' B' C' D' 例2 把四边形 ABCD 缩小到原来的 1/2. (1) 在四边形外任选一点 O (如图);(2) 分别在线段 OA,OB,OC,OD 上取点 A' 、B' 、 C' 、D' ,使得 ; 1 2 OA' OB' OC' OD' OA OB OC OD 利用位似,可 以将一个图形 放大或缩小 思考: 对于上面的问题,还有其他方法吗?如果在四边 形外任选一个点 O,分别在 OA,OB,OC,OD 的反 向延长线上取 A′ ,B′ ,C′,D′,使得 呢?如果点 O 取在四边形 ABCD 内部 呢?分别画出这时得到的图形. OA' OB' OA OB1 2 OC' OD' OC OD O D A B C A' B' C' D' O D A B C A' B' C' D' 如图,△ABC. 根据要求作△A'B'C',使△A' B' C' ∽△ABC,且相似比为 1 : 5. (1) 位似中心在△ABC的一条边AB上; 练一练 A CB O ● A′ B′ C′ ● ● 假设位似中心点 O 为 AB 中点,点 O 位置如图所 示. 根据相似比可确定 A′, B′,C′ 的位置.● (2) 以点 C 为位似中心. C A B A′ B′ ( C′ ) ● ● ● ◑ 画位似图形的一般步骤: ① 确定位似中心; ② 分别连接并延长位似中心和能代表原图的关 键点; ③ 根据相似比,确定能代表所作的位似图形的 关键点; ④ 顺次连接上述各点,得到放大或缩小的图形. 归纳: ◑ 利用位似进行作图的关键是确定位似中心和 关键点. ◑ 位似分为内位似和外位似,内位似的位似中 心在连接两个对应点的线段上;外位似的位 似中心在连接两个对应点的线段之外. A B C D 1. 选出下面不同于其他三组的图形 ( )B 随堂练习 2. 如图,正五边形 FGHMN 与正五边形 ABCDE 是位 似图形,若AB : FG = 2 : 3,则下列结论正确的是 ( ) A. 2 DE = 3 MN B. 3 DE = 2 MN C. 3∠A = 2∠F D. 2∠A = 3∠F B A B E C D N F G H M 3. 下列说法: ①位似图形一定是相似图形;②相似图形一定是位 似图形;③两个位似图形若全等,则位似中心在两 个图形之间;④若五边形ABCDE与五边形A′B′C′D′E′ 位似,则其中 △ABC 与 △A′B′C′ 也是位似的,且位 似比相等. 其中正确的有 . ①④ 4. 如图,△ABC与△DEF是位似图形,位似比为 2 : 3,已知 AB=4,则 DE 的长为_____. 6 5.已知点O在△ABC内,以点O为位似中心画一个三角 形,使它与△ABC位似,且位似比为1:2. A B C 解:画射线OA,OB,OC;在 射线OA,OB,OC上分别取点 D,E,F,使OA = 2OD,OB = 2OE,OC = 2OF;顺序连接 D,E,F,使△DEF与△ABC位 似,位似比为1:2. D E F 6. 如图,F 在 BD 上,BC,AD 相交于点 E,且 AB∥CD∥EF, (1) 图中有哪几对位似三角形? 选其中一对加 以证明; 答案:△DFE 与 △DBA,△BFE 与 △BDC, △AEB 与 △DEC 都是位似图形;证明略. (2) 若 AB=2,CD=3,求 EF 的长. 解:∵ △BFE ∽△BDC,△AEB ∽△DEC, AB=2,CD=3, 2 3 ,AB BE DC EC ∴ 2 5 ,BE EF BC DC ∴ 解得 6 5 EF . 位似的概念及画法 位似图形的概念 位似图形的性质 画位似图形 课堂小结查看更多