2021年中考数学核心考点强化突破：函数的实际应用问题

2021年中考数学核心考点强化突破：函数的实际应用问题

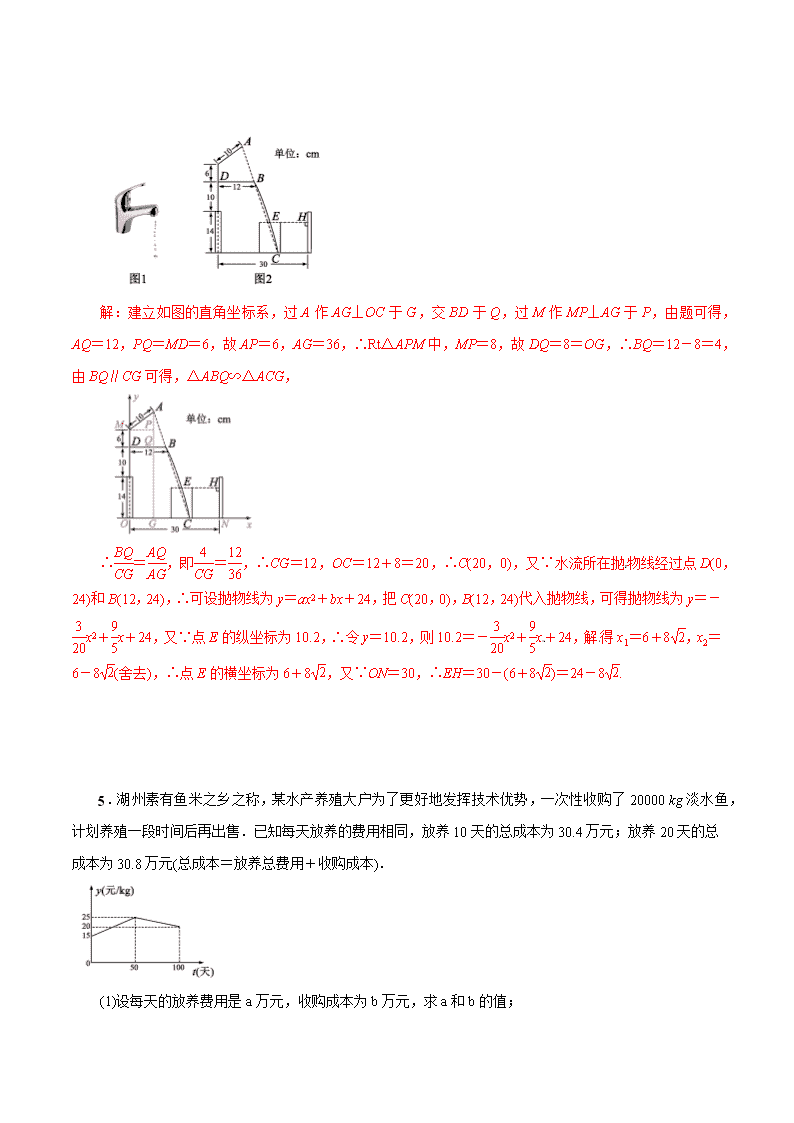
‎2021年中考数学核心考点强化突破：函数的实际应用问题 ‎ 类型1　方案与最值问题 ‎1．江南农场收割小麦，已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷，2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷．‎ ‎(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷？‎ ‎(2)大型收割机每小时费用为300元，小型收割机每小时费用为200元，两种型号的收割机一共有10台，要求2小时完成8公顷小麦的收割任务，且总费用不超过5400元，有几种方案？请指出费用最低的一种方案，并求出相应的费用．‎ 解析：(1)设每台大型收割机1小时收割小麦x公顷，每台小型收割机1小时收割小麦y公顷，根据题意得：，解得：.答：略．‎ ‎(2)设大型收割机有m台，总费用为w元，则小型收割机有(10－m)台，根据题意得：w＝300×2m＋200×2(10－m)＝200m＋4000.∵2小时完成8公顷小麦的收割任务，且总费用不超过5400元，∴解得：5≤m≤7，∴有三种不同方案．∵w＝200m＋4000中，200＞0，∴w值随m值的增大而增大，∴当m＝5时，总费用取最小值，最小值为5000元．答：有三种方案，当大型收割机和小型收割机各5台时，总费用最低，最低费用为5000元．‎ ‎2．某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙(墙足够长)，已知计划中的建筑材料可建围墙的总长为50 m．设饲养室长为x(m)，占地面积为y(m2)．‎ ‎(1)如图1，问饲养室长x为多少时，占地面积y最大？‎ ‎(2)如图2，现要求在图中所示位置留2 m宽的门，且仍使饲养室的占地面积最大，小敏说：“只要饲养室长比(1)中的长多2 m就行了．”请你通过计算，判断小敏的说法是否正确．‎ 解：(1)∵y＝x·＝－(x－25)2＋，∴当x＝25时，占地面积最大，即饲养室长x为25 m时，占地面积y最大；‎ ‎(2)∵y＝x·＝－(x－26)2＋338，∴当x＝26时，占地面积最大，即饲养室长x为26 m时，‎ 占地面积y最大；∵26－25＝1≠2，∴小敏的说法不正确．‎ ‎3．(2017·河南)学校“百变魔方”社团准备购买A，B两种魔方，已知购买2个A种魔方和6个B种魔方共需130元，购买3个A种魔方和4个B种魔方所需款数相同．‎ ‎(1)求这两种魔方的单价；‎ ‎(2)结合社员们的需求，社团决定购买A，B两种魔方共100个(其中A种魔方不超过50个)．某商店有两种优惠活动，如图所示．请根据以上信息，说明选择哪种优惠活动购买魔方更实惠．‎ 解：(1)设A种魔方的单价为x元/个，B种魔方的单价为y元/个，根据题意得：，解得：.‎ 答：A种魔方的单价为20元/个，B种魔方的单价为15元/个．‎ ‎(2)设购进A种魔方m个(0≤m≤50)，总价格为w元，则购进B种魔方(100－m)个，根据题意得：w活动一＝20m×0.8＋15(100－m)×0.4＝10m＋600；w活动二＝20m＋15(100－m－m)＝－10m＋1500.当w活动一＜w活动二时，有10m＋600＜－10m＋1500，解得：m＜45；当w活动一＝w活动二时，解得：m＝45；当w活动一＞w活动二时，解得：45＜m≤50.综上所述：当45＜m≤50时，选择活动一购买魔方更实惠；当m＝45时，选择两种活动费用相同；当m＞45时，选择活动二购买魔方更实惠．‎ 类型2　建立函数模型问题 ‎4．小明家的洗手盆上装有一种抬启式水龙头(如图1)，完全开启后，水流路线呈抛物线，把手端点A，出水口B和落水点C恰好在同一直线上，点A至出水管BD的距离为12 cm，洗手盆及水龙头的相关数据如图2所示，现用高10.2 cm的圆柱型水杯去接水，若水流所在抛物线经过点D和杯子上底面中心E，则点E到洗手盆内侧的距离EH为__24－8__cm.‎ 解：建立如图的直角坐标系，过A作AG⊥OC于G，交BD于Q，过M作MP⊥AG于P，由题可得，AQ＝12，PQ＝MD＝6，故AP＝6，AG＝36，∴Rt△APM中，MP＝8，故DQ＝8＝OG，∴BQ＝12－8＝4，由BQ∥CG可得，△ABQ∽△ACG，‎ ‎∴＝，即＝，∴CG＝12，OC＝12＋8＝20，∴C(20，0)，又∵水流所在抛物线经过点D(0，24)和B(12，24)，∴可设抛物线为y＝ax2＋bx＋24，把C(20，0)，B(12，24)代入抛物线，可得抛物线为y＝－x2＋x＋24，又∵点E的纵坐标为10.2，∴令y＝10.2，则10.2＝－x2＋x＋24，解得x1＝6＋8，x2＝6－8(舍去)，∴点E的横坐标为6＋8，又∵ON＝30，∴EH＝30－(6＋8)＝24－8.[来源:Zxxk.Com]‎ ‎[来源:Zxxk.Com]5．湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了20000 kg淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元(总成本＝放养总费用＋收购成本)．‎ ‎(1)设每天的放养费用是a万元，收购成本为b万元，求a和b的值；‎ ‎(2)设这批淡水鱼放养t天后的质量为m(kg)，销售单价为y元/ kg.根据以往经验可知：m与t的函数关系为m＝；y与t的函数关系如图所示．‎ ‎①分别求出当0≤t≤50和50＜t≤100时，y与t的函数关系式；‎ ‎②设将这批淡水鱼放养t天后一次性出售所得利润为W元，求当t为何值时，W最大？并求出最大值．(利润＝销售总额－总成本)‎ 解：(1)由题意，得：，解得.[来源:学§科§网Z§X§X§K]‎ ‎(2)①当0≤t≤50时，设y与t的函数解析式为y＝k1t＋n1，将(0，15)、(50，25)代入，可求得y与t的函数解析式为：y＝t＋15；当50＜t≤100时，设y与t的函数解析式为y＝k2t＋n2，将点(50，25)、(100，20)代入，可求得y与t的函数解析式为：y＝－t＋30；②由题意，当0≤t≤50时，W＝20000(t＋15)－(400t＋300000)＝3600t，∵3600＞0，∴当t＝50时，W最大＝180000(元)；当50＜t≤100时，W＝(100t＋15000)(－t＋30)－(400t＋300000)＝－10(t－55)2＋180250，∵－10＜0，∴当t＝55时，W最大＝180250(元)．‎ 综上所述，放养55天时，W最大，最大值为180250元．‎