- 2021-11-10 发布 |
- 37.5 KB |
- 11页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
苏教版数学九年级上册课件2-5直线与圆的位置关系(3)
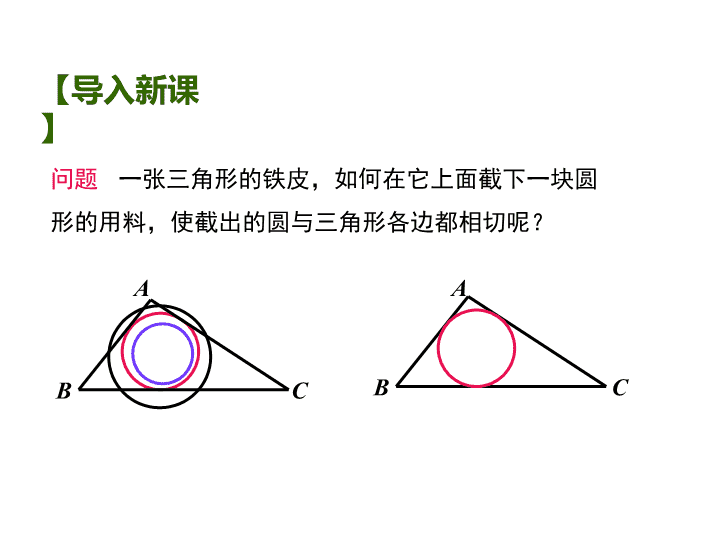
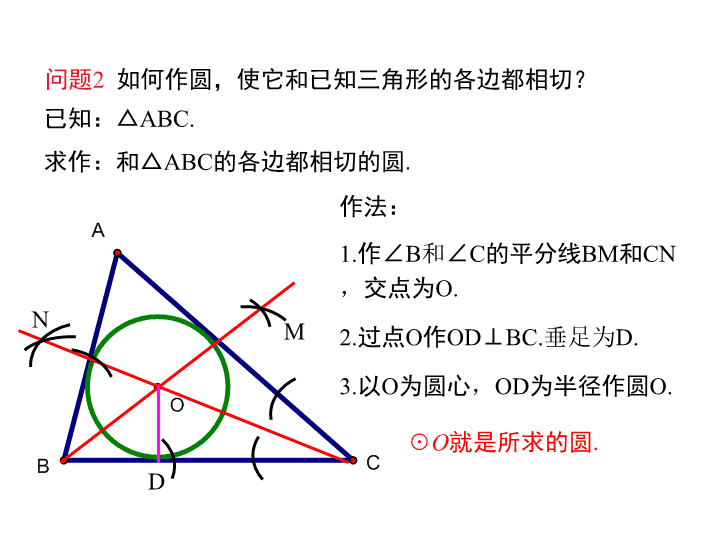
2.5直线与圆的位置关系(3) 问题 一张三角形的铁皮,如何在它上面截下一块圆 形的用料,使截出的圆与三角形各边都相切呢? A B C A B C 【导入新课】 问题2 如何作圆,使它和已知三角形的各边都相切? 已知:△ABC. 求作:和△ABC的各边都相切的圆. A B C O MN D 作法: 1.作∠B和∠C的平分线BM和CN, 交点为O. 2.过点O作OD⊥BC.垂足为D. 3.以O为圆心,OD为半径作圆O. ☉O就是所求的圆. 1.与三角形各边都相切的圆叫做这个三角形的内切圆. 2.三角形内切圆的圆心叫做这个三角形的内心. 3.这个三角形叫做这个圆的外切三角形. 4.三角形的内心就是三角形三条角平分线的交点. B ┐ A C I ┐ ┐ D E F 三角形的内心到三角形的三边的距离相等. ☉O是△ABC的内切圆, 点O是△ABC的内心, △ABC是☉O的外切三角形. 【讲授新课】 名称 确定方法 图形 性质 外心:三 角形外接 圆的圆心 内心:三 角形内切 圆的圆心 三角形三边 中垂线的交 点 1.OA=OB=OC 2.外心不一定在三 角形的内部. 三角形三条 角平分线的 交点 1.到三边的距离相 等; 2.OA、OB、OC分 别平分∠BAC、 ∠ABC、∠ACB 3.内心在三角形内 部. A B O A B C O 填一填 例1 △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、 F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长. 想一想:图中你能找出哪些相等 的线段?理由是什么? A C B E D F O 【例题讲解】 解:设AF=xcm,则AE=xcm. ∴CE=CD=AC-AE=9-x(cm), BF=BD=AB-AF=13-x(cm). 由 BD+CD=BC,可得 (13-x)+(9-x)=14, ∴ AF=4(cm),BD=9(cm),CE=5(cm). 方法小结:关键是熟练运用切线长定理,将相等线段转 化集中到某条边上,从而建立方程. 解得 x=4. △ABC的内切圆☉O与三边分别切于D、E、F三点,如图, 已知AF=3,BD+CE=12,则△ABC的周长是 . 【练习】 30 直角三角形的两直角边分别是3cm ,4cm,试问: (1)它的外接圆半径是 cm;内切圆半径是 cm? (2)若移动点O的位置,使☉O保持与△ABC的边AC、BC都相 切,求☉O的半径r的取值范围. · A BC E D F O 5 1 解:如图所示,设与BC、AC相切的最大圆与BC、 AC的切点分别为B、D,连接OB、OD,则四边形 BODC为正方形. · A B OD C ∴OB=BC=3, ∴半径r的取值范围为0<r≤3. 【小结】 三角形 内切圆 运用切线长定理,将相等线段 转化集中到某条边上,从而建 立方程. 有关概念 内心概念及性质 应 用查看更多