2019-2020学年山东青岛九年级下数学期中试卷

2019-2020学年山东青岛九年级下数学期中试卷

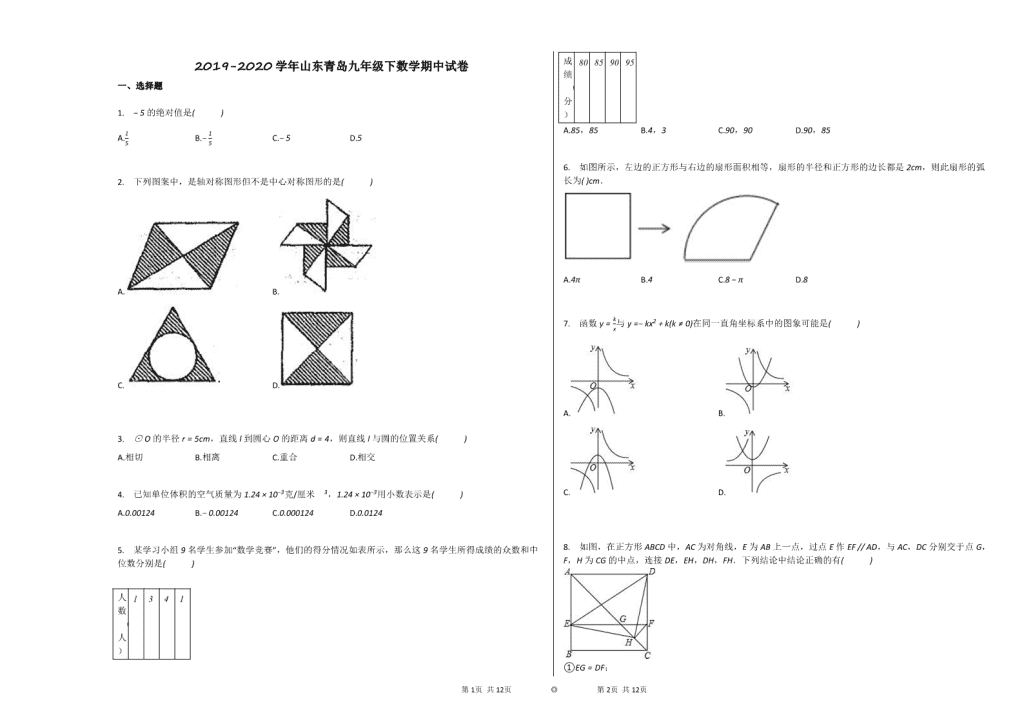
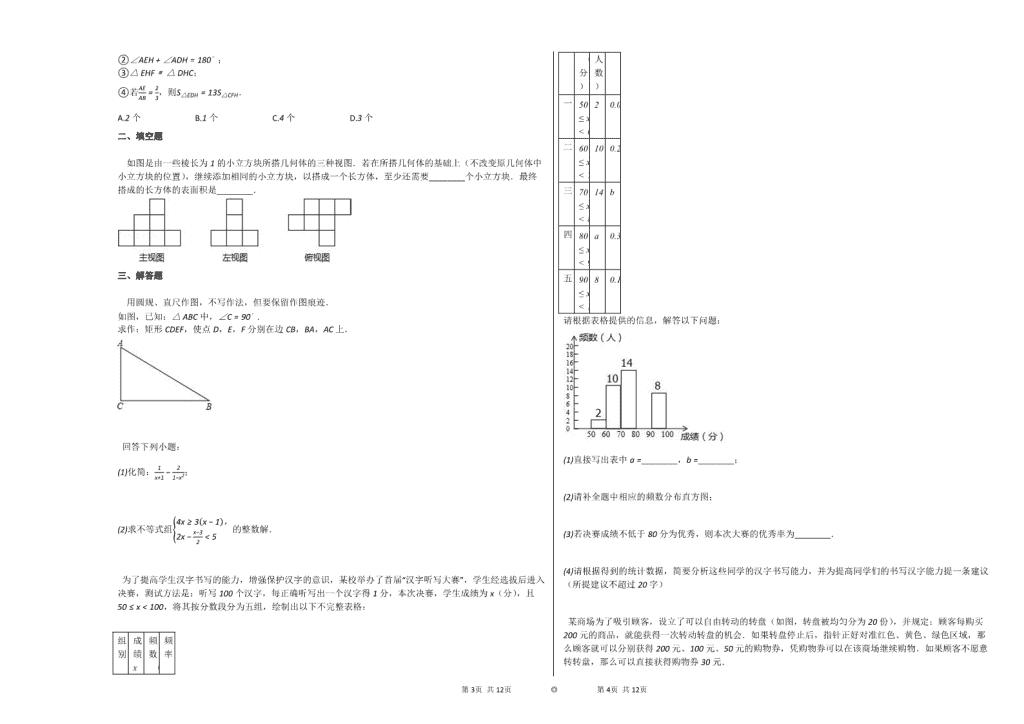
‎2019-2020学年山东青岛九年级下数学期中试卷 一、选择题 ‎ ‎ ‎1. ‎−5‎的绝对值是‎(‎        ‎)‎ ‎ A.‎1‎‎5‎ B.‎−‎‎1‎‎5‎ C.‎−5‎ D.‎‎5‎ ‎ ‎ ‎2. 下列图案中，是轴对称图形但不是中心对称图形的是‎(‎        ‎)‎ ‎ A. B. C. D. ‎ ‎ ‎ ‎3. ‎⊙O的半径r=5cm，直线l到圆心O的距离d=4‎，则直线l与圆的位置关系‎(‎        ‎)‎ ‎ A.相切 B.相离 C.重合 D.相交 ‎ ‎ ‎4. 已知单位体积的空气质量为‎1.24×‎‎10‎‎−3‎克/厘米‎​‎‎3‎，‎1.24×‎‎10‎‎−3‎用小数表示是‎(‎        ‎)‎ ‎ A.‎0.00124‎ B.‎−0.00124‎ C.‎0.000124‎ D.‎‎0.0124‎ ‎ ‎ ‎5. 某学习小组‎9‎名学生参加“数学竞赛”，他们的得分情况如表所示，那么这‎9‎名学生所得成绩的众数和中位数分别是‎(‎        ‎)‎ ‎ 人数（人）‎ ‎1‎ ‎3‎ ‎4‎ ‎1‎ 成绩（分）‎ ‎80‎ ‎85‎ ‎90‎ ‎95‎ A.‎85‎，‎85‎ B.‎4‎，‎3‎ C.‎90‎，‎90‎ D.‎90‎，‎‎85‎ ‎ ‎ ‎6. 如图所示，左边的正方形与右边的扇形面积相等，扇形的半径和正方形的边长都是‎2cm，则此扇形的弧长为‎(‎ ‎)cm． ‎ A.‎4π B.‎4‎ C.‎8−π D.‎‎8‎ ‎ ‎ ‎7. 函数y=‎kx与y=−kx‎2‎+k(k≠0)‎在同一直角坐标系中的图象可能是‎(‎        ‎)‎ ‎ A. B. C. D. ‎ ‎ ‎ ‎8. 如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF // AD，与AC，DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论中结论正确的有‎(‎        ‎)‎ ①EG=DF； ②‎∠AEH+∠ADH=‎‎180‎‎∘‎； ③‎△EHF≅△DHC； ④若AEAB‎=‎‎2‎‎3‎，则S‎△EDH‎=13‎S‎△CFH． ‎ A.‎2‎个 B.‎1‎个 C.‎4‎个 D.‎3‎个 二、填空题 ‎ ‎ 第9页 共12页 ◎ 第10页 共12页 ‎ 如图是由一些棱长为‎1‎的小立方块所搭几何体的三种视图．若在所搭几何体的基础上（不改变原几何体中小立方块的位置），继续添加相同的小立方块，以搭成一个长方体，至少还需要________个小立方块．最终搭成的长方体的表面积是________． ‎ 三、解答题 ‎ ‎ ‎ 用圆规、直尺作图，不写作法，但要保留作图痕迹． 如图，已知：‎△ABC中，‎∠C=‎‎90‎‎∘‎. 求作：矩形CDEF，使点D，E，F分别在边CB，BA，AC上． ‎ ‎ ‎ ‎ 回答下列小题： ‎ ‎(1)‎化简：‎1‎x+1‎‎−‎‎2‎‎1−‎x‎2‎；‎ ‎ ‎ ‎(2)‎求不等式组‎4x≥3x−1‎，‎‎2x−x−3‎‎2‎<5‎的整数解．‎ ‎ ‎ ‎ 为了提高学生汉字书写的能力，增强保护汉字的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试方法是：听写‎100‎个汉字，每正确听写出一个汉字得‎1‎分，本次决赛，学生成绩为x（分），且‎50≤x<100‎，将其按分数段分为五组，绘制出以下不完整表格： ‎ 组别 成绩x（分）‎ 频数（人数）‎ 频率 一 ‎50≤x<60‎ ‎2‎ ‎0.04‎ 二 ‎60≤x<70‎ ‎10‎ ‎0.2‎ 三 ‎70≤x<80‎ ‎14‎ b 四 ‎80≤x<90‎ a ‎0.32‎ 五 ‎90≤x<100‎ ‎8‎ ‎0.16‎ 请根据表格提供的信息，解答以下问题： ‎ ‎(1)‎直接写出表中a=‎________，b=‎________；‎ ‎ ‎ ‎(2)‎请补全题中相应的频数分布直方图；‎ ‎ ‎ ‎(3)‎若决赛成绩不低于‎80‎分为优秀，则本次大赛的优秀率为________．‎ ‎ ‎ ‎(4)‎请根据得到的统计数据，简要分析这些同学的汉字书写能力，并为提高同学们的书写汉字能力提一条建议（所提建议不超过‎20‎字）‎ ‎ ‎ ‎ 某商场为了吸引顾客，设立了可以自由转动的转盘（如图，转盘被均匀分为‎20‎份），并规定：顾客每购买‎200‎元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得‎200‎元、‎100‎元、‎50‎元的购物券，凭购物券可以在该商场继续购物．如果顾客不愿意转转盘，那么可以直接获得购物券‎30‎元． ‎ ‎(1)‎求转动一次转盘获得购物券的概率；‎ ‎ ‎ ‎(2)‎转转盘和直接获得购物券，你认为哪种方式对顾客更合算？‎ ‎ ‎ 第9页 共12页 ◎ 第10页 共12页 ‎ 如图，小明想测索道的长度．他在B处仰望山顶A，测得仰角‎∠B=‎‎31‎‎∘‎，再往山的方向（水平方向）前进‎80m至索道口C处，沿索道方向仰望山顶，测得仰角‎∠ACE=‎‎39‎‎∘‎．求索道AC的长（结果精确到整数）． （参考数据：tan‎31‎‎∘‎≈‎‎3‎‎5‎，sin‎31‎‎∘‎≈‎‎1‎‎2‎，tan‎39‎‎∘‎≈‎‎9‎‎11‎，sin‎39‎‎∘‎≈‎‎7‎‎11‎） ‎ ‎ ‎ ‎ 某校在如意商场购买甲、乙两种不同足球，购买甲种足球共花费‎2000‎元，购买乙种足球共花费‎1400‎元，购买甲种足球数量是购买乙种足球数量的‎2‎倍，且购买一个乙种足球比购买一个甲种足球多花‎20‎元． ‎ ‎(1)‎求购买一个甲种足球、一个乙种足球分别需要多少元；‎ ‎ ‎ ‎(2)‎若当这所学校决定再次购买甲、乙两种足球共‎50‎个时，恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了‎10%‎，乙种足球售价比第一次购买时降低了‎10%‎，如果此次购买甲、乙两种足球的总费用不超过‎2900‎元，那么这所学校最多可购买多少个乙种足球？‎ ‎ ‎ ‎ 如图，已知平行四边形ABCD，延长AD到E，使DE=AD，连接BE与DC交于O点． ‎ ‎(1)‎求证：‎△BOC≅△EOD；‎ ‎ ‎ ‎(2)‎当‎△ABE满足什么条件时，四边形BCED是菱形？证明你的结论．‎ ‎ ‎ ‎ 某商场经营某种品牌的玩具，购进时的单价是‎30‎元，根据市场调查：在一段时间内，销售单价是‎40‎元时，销售量是‎600‎件，而销售单价每涨‎1‎元，就会少售出‎10‎件玩具. ‎ ‎(1)‎设该种品牌玩具的销售单价为x元，请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元；‎ ‎ ‎ ‎(2)‎在‎(1)‎问条件下，若商场获得了‎10000‎元销售利润，求该玩具销售单价x应定为多少元；‎ ‎ ‎ ‎(3)‎在‎(1)‎问条件下，若玩具厂规定该品牌玩具销售单价不低于‎45‎元，且商场要完成不少于‎480‎件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？‎ ‎ ‎ ‎ 问题提出：将正m边形‎(m≥3)‎不断向外扩展，每扩展一个正m边形每条边上的点的个数（以下简称“点数”）就增加一个，则n个正m边形的点数总共有多少个？ 问题探究：为了解决上面的问题，我们将采取将一般问题特殊化的策略，先从简单和具体的情形入手： ‎ ‎(1)‎探究一：n个正三角形的点数总共有多少个？ ‎ 如图‎1−1‎，‎1‎个正三角形的点数总共有‎3‎个；如图‎1−2‎，‎2‎个正三角形的点数总共有‎6‎个；如图‎1−3‎，‎3‎个正三角形的点数总共有‎10‎个；…；n个正三角形的点数总共有________个．‎ ‎ ‎ ‎(2)‎探究二：n个正四边形的点数总共有多少个？ ‎ 如图‎2−1‎，‎1‎个正四边形的点数总共有‎4‎个；如图‎2−2‎，‎2‎个正四边形的点数总共有‎9‎个；‎ 如图‎2−3‎，连接AC，得到两个三角形‎△ABC和‎△ADC，这两个三角形相同之处在于，BC边与CD边都有相同个数的点，即‎4‎个点，并且与BC，CD平行的边上依次减少一个点直至顶点A，每个三角形都有‎10‎个点，两个三角形就是‎2×10‎个点．因为这两个三角形在AC上有‎4‎个点重合，所以‎3‎个正四边形的点数总共有‎2×10−4=‎‎16‎（个）．‎ 如图‎2−4‎，‎4‎个正四边形的点数总共有________个；……n个正四边形的点数总共有________个．‎ ‎ ‎ ‎(3)‎探究三：n个正五边形的点数总共有多少个？ ‎ 类比探究二的方法，求‎4‎个正五边形的点数总共有多少个？并叙述你的探究过程．‎ n个正五边形的点数总共有________个．‎ ‎ ‎ 第9页 共12页 ◎ 第10页 共12页 ‎(4)‎探究四：n个正六边形的点数总共有________个． ‎ 问题解决：n个正m边形的点数总共有________个．‎ 实际应用：若‎99‎个正m边形的点数总共有‎39700‎个，求m的值．‎ 第9页 共12页 ◎ 第10页 共12页 参考答案与试题解析 ‎2019-2020学年山东青岛九年级下数学期中试卷 一、选择题 ‎1.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 绝对值 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎2.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 中心较称图腾 轴正算图形 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎3.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 直线与都连位置关系 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎4.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 科学记正测--原数 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎5.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 众数 中位数 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎6.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 扇形体积硫计算 弧因斯计算 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎7.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二次来数的斗象 反比例射数的图放 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎8.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 全根三烛形做给质与判定 等腰于角三旋形 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 二、填空题 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 几何体的存面积 由三视正活断几何体 第9页 共12页 ◎ 第10页 共12页 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 三、解答题 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 作图常复占作图 矩来兴性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 分式表乘弹运算 一元三次实等另组每整数解 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 频数（率）分布直方水 频数（常）换布表 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 概水常式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 解直角明角念的应用备仰角俯城问题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 一元都次特等水的实常应用 分式较程的腾用 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 菱因顿判定 平行四表形型性质 全等三表形木判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 二次表数擦应用 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 规律型：三形的要化类 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 第9页 共12页 ◎ 第10页 共12页