- 2021-11-10 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
概率初步(4)25.2 用列举法求概率
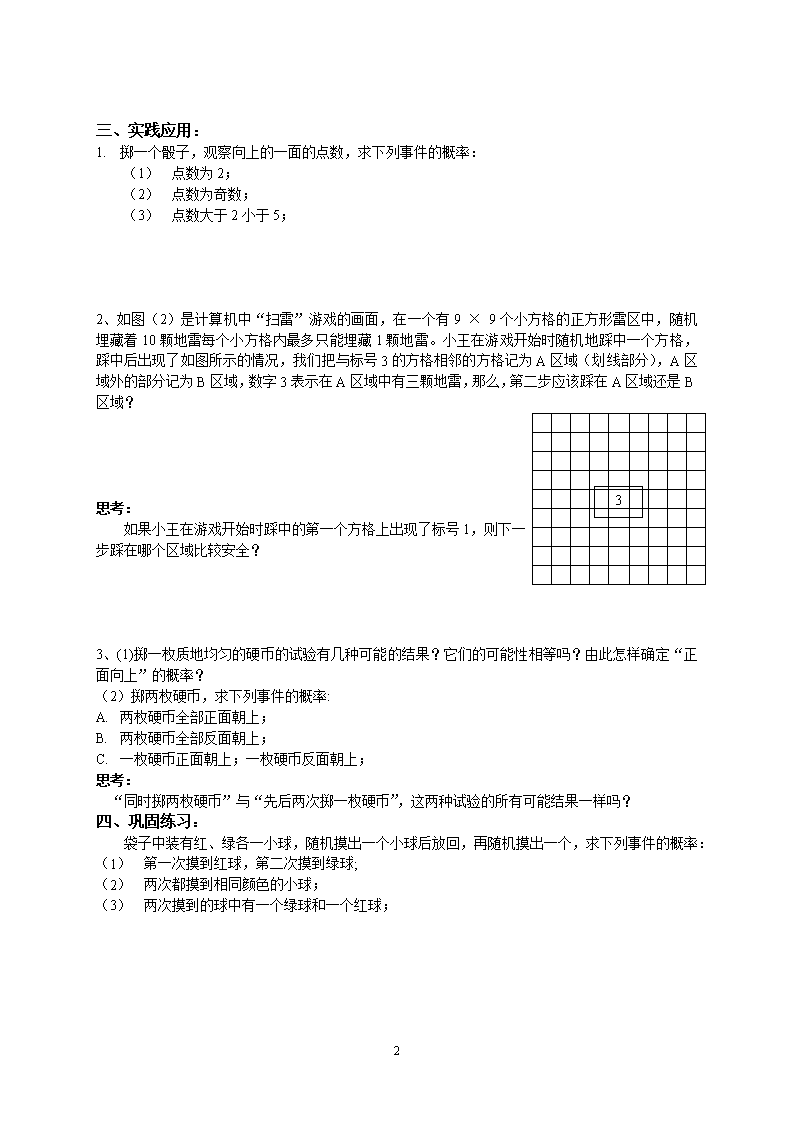
第二十五章 概率初步 年级:九年级 内容:25.2用列举法求概率(第1课时) 课型:新授 执笔: 审核:孙万生 定稿: 使用时间: 学习目标: 1. 理解 P(A)= (在一次试验中有 n 种可能的结果,其中 A 包含 m 种)的意义。 2.应用 P(A)= 解决一些实际问题。 学习重点:理解 P(A)= 并运用它解决实际问题。 学习难点:通过试验理解 P(A)= 并运用它解决一些具体问题。 学习过程: 一、 课前准备: (1) 概率是什么? (2) P(A) 的取值范围是什么? (3) A是必然事件,B是不可能事件,C是随机事件,请你画出数轴把三个量表示出来。 二、试验探究: 试验1 从分别标有1、2、3、4、5号的5根纸签中随机抽取一根,抽出的签上的号码有( )种可能,即( )由于纸签的形状、大小相同,又是随机抽取的,所以我们认为:每个号码抽到的可能性( )都是( )。 试验2 掷一个骰子,向上一面的点数有( )种可能,即( )由于骰子的构造、质地均匀,又是随机掷出的所以我们断言:每种结果的可能性( )都是( )。 观察与思考: 以上两个试验有两个共同特点: 1.( ) 2.( ) 如何分析出此类试验中事件的概率? 归纳: 一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为P(A)=( )。且( )≤ P(A) ≤ ( )。 4 三、实践应用: 1. 掷一个骰子,观察向上的一面的点数,求下列事件的概率: (1) 点数为2; (2) 点数为奇数; (3) 点数大于2小于5; 2、如图(2)是计算机中“扫雷”游戏的画面,在一个有9 × 9个小方格的正方形雷区中,随机埋藏着10颗地雷每个小方格内最多只能埋藏1颗地雷。小王在游戏开始时随机地踩中一个方格,踩中后出现了如图所示的情况,我们把与标号3的方格相邻的方格记为A区域(划线部分),A区域外的部分记为B区域,数字3表示在A区域中有三颗地雷,那么,第二步应该踩在A区域还是B区域? 3 思考: 如果小王在游戏开始时踩中的第一个方格上出现了标号1,则下一步踩在哪个区域比较安全? 3、(1)掷一枚质地均匀的硬币的试验有几种可能的结果?它们的可能性相等吗?由此怎样确定“正面向上”的概率? (2)掷两枚硬币,求下列事件的概率: A. 两枚硬币全部正面朝上; B. 两枚硬币全部反面朝上; C. 一枚硬币正面朝上;一枚硬币反面朝上; 思考: “同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗? 四、巩固练习: 袋子中装有红、绿各一小球,随机摸出一个小球后放回,再随机摸出一个,求下列事件的概率: (1) 第一次摸到红球,第二次摸到绿球; (2) 两次都摸到相同颜色的小球; (3) 两次摸到的球中有一个绿球和一个红球; 4 五、学习小结: 这节课有哪些收获?说说自己哪些不懂,与同学交流一下。 六、自我检测 1.柜子里有20双鞋,取出左脚穿的一只鞋的概率为( ) A B C D不确定 2.投掷一枚质地均匀的骰子,点数小于5的概率为( ) A B C D 3.盒子里有8个除颜色外,其它完全相同的球,若摸到红色的球的概率为3/4 ,则其中红球的个数是( ) A 8 B6 C4 D无法确定 4.数学考试中的选择题一般都是单项选择,即在A、B、C、D四个备选答案中只有一个是正确的,这种选择题任意选一个答案,正确的概率是( ) 5.某中学八年级(1)班有55名学生参加期末数学考试,其中45人及格,从所有考卷中任意抽取一张,抽中不及格的概率为( ) 6.一个袋中装有2个白球,4个红球,6个黄球,这些球除颜色不同外,其它完全相同,从袋中任意摸出一个球,求下列事件的概率 (1). 摸出红球 (2). 摸出白球 (3).摸出不是黄球 ※ 广告牌上“丽晶大酒店”几个字是霓虹灯,几个字一个接一个地亮起来,直至全部亮起来再循环,则路人一眼望去能够看全的概率为多少? 七、巩固提高: 1、袋中装有若干个红球和若干个黄球,它们除了颜色外都相同,任意从中摸出一个球,摸到红球的概率是. (1)若袋中共有8个球,需要几个红球? (2)若袋中有9个红球,则还需要几个黄球? (3)自己设计一个摸球游戏,使摸到红球的概率是. 4 2.判断下面的结论对否,并说明为什么? 两人各掷一枚硬币,“同时出现正面”的概率等于, 则“不出现正面”的概率等于 1-=。 4查看更多