九年级数学上册 43 相似多边形 新版北师大版

九年级数学上册 43 相似多边形 新版北师大版

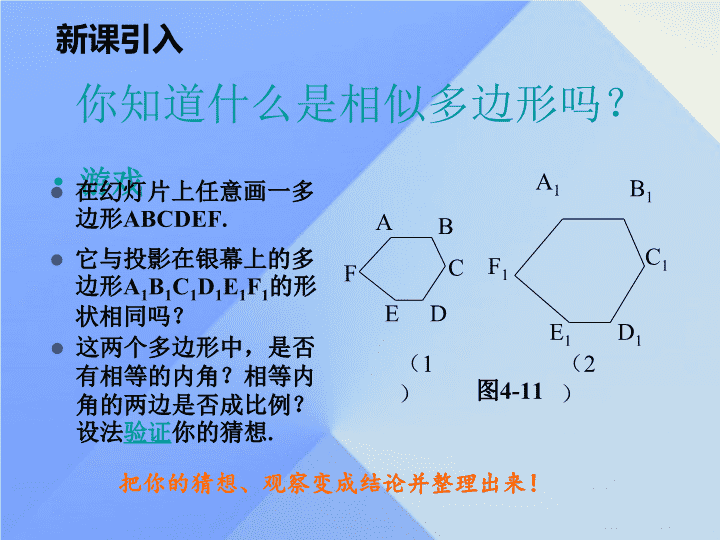
相似多边形 你知道什么是相似多边形吗？ 游戏 把你的猜想、观察变成结论并整理出来！ 这两个多边形中，是否有相等的内角？相等内角的两边是否成比例？设法 验证 你的猜想 . （ 1 ） B C D E F A B 1 C 1 D 1 E 1 F 1 A 1 （ 2 ） 图 4-11 在幻灯片上任意画一多边形 ABCDEF. 它与投影在银幕上的多边形 A 1 B 1 C 1 D 1 E 1 F 1 的形状相同吗？ 新课引入 我是叠合法操作的？ （ 1 ） B C D E F A B 1 C 1 D 1 E 1 F 1 A 1 （ 2 ） 图 4-11 B C D E F A B C D E F A B C D E F A B C D E F A B C D E F A B C D E F A 我是用量角器和刻度尺度量的？ 我是用 …… ？ 结论： 六边形 ABCDEF 与六边形 A 1 B 1 C 1 D 1 E 1 F 1 是形状相同的图形； 它们的六个角都 分别相等 ，称为 对应角 ；六条边的比都 相等 ，称为 对应边 . 形状相同的图形，它们的对应角有怎样的关系？对应边呢？ 记作如：六边形 ABCDEF∽ 六边形 A 1 B 1 C 1 D 1 E 1 F 1 （ 1 ） B C D E F A B 1 C 1 D 1 E 1 F 1 A 1 （ 2 ） 图 4-11 请同学们欣赏课本 例题 . 结论： 各 对应角相等 、各 对应边成比例 的两个多边形叫做 相似多边形 （ similar polygons ）； 记两个多边形相似时，要把 对应顶点 的字母写在 对应的位置 . 新课讲解 例 下列每组图形形状相同，它们的对应角有怎样的关系？对应边呢？ 从例题的解答中，你获得了那些信息？ （ 1 ）正三角形 ABC 与正三角形 DEF ； 解： （ 1 ）由于正三角形每个角都等于 60 0 ，所以∠ A=∠D= 60 0 ，∠ B=∠E= 60 0 ， ∠ C=∠F= 60 0 ； （ 1 ） B C D E F A 由于正三角形三边都相等，所以 例题分析 两题过后，你又有什么收获？ （ 2 ）正方形 ABC D 和正方形 EFGH. B C D E F A （ 2 ） H G 解： （ 2 ）由于正方形每个角都是直角，所以∠ A=∠E= 90 0 ， ∠ B=∠F= 90 0 ， ∠ C=∠G= 90 0 ， ∠ D=∠H= 90 0 ； 由于正方形四边相等，所以 相似多边形对应边的比叫做相似比（ similarity ratio ） 你注意到没有，相似比与叙述的顺序的关系？ （ 1 ） B C D E F A B 1 C 1 D 1 E 1 F 1 A 1 （ 2 ） 图 4-11 如：六边形 ABCDEF∽ 六边形 A 1 B 1 C 1 D 1 E 1 F 1 AB ： A 1 B 1 =BC ： B 1 C 1 =CD ： C 1 D 1 =DE ： D 1 E 1 =EF ： E 1 F 1 =FA ： F 1 A 1 =1 ： 2, 因此，六边形 ABCDEF 与六边形 A 1 B 1 C 1 D 1 E 1 F 1 的相似比为 K 1 ，六边形 A 1 B 1 C 1 D 1 E 1 F 1 与六边形 ABCDEF 的相似比为 K 1 =2. 新课讲解 议一议——返过来会怎样？ 如果两个多边形想似，那么它们的对应角有什么关系？对应边呢？ 相似多边形的对应角相等，对应边成比例 . 看一看，议一议——合作交流 （ 1 ）、观察下面两组图形，图 4-12 （ 1 ）中的两个图形相似吗？为什么？图 4-12 （ 2 ）中的两个图形呢？与同伴交流 . （ 2 ）、如果两个多边形不相似，那么它们的各角可能对应相等吗？它们的各边可能对应成比例吗？ 10 10 12 12 10 10 8 12 （ 1 ） （ 2 ） 图 4-12 做一做——你猜对了吗？ 直观有时候是不可靠的 . 镶在其外围的木质边框 7.5cm. 边框的内外边缘所成的矩形相似吗？为什么？ 一块长 3m 、宽 1.5m 的矩形黑板 . 学习是件很充实的事！ 它们不相似，因为对应边不成比例 . 读一读——纸张的大小 见课本 《 读一读 》 用你的学习用纸，来实地操作验证一下！ 生活中的数学无处不在，只要你愿意去发现，其乐无穷 . 课堂练习 1 、右面两个矩形相似，求它们对应边的比 . 2 、如图，两个正六边形的边长分别为 a 和 b ，它们相似吗？为什么？ 3 、 如图，矩形的草坪长 20m ，宽 10m ，沿草坪四周外围有 1m 的环行小路，小路的内外边缘所成的矩形相似吗？ 2 3 不相似 . 因为对应边不成比例 . 2∶3 相似 . 理由是：各对应角相等，各对应边成比例 . 课堂小结 1. 各对应角相等、各对应边成比例的两个多边形叫做相似多边形（ similar polygons ）； 2. 相似多边形对应边的比叫做相似比（ similarity ratio ） 5. 如果两个多边形不相似，那么它们的各角可能对应相等，它们的各边可能对应成比例 . 3. 相似比与叙述的顺序有关 . 6. 直观有时候是不可靠的 . 4. 相似多边形的对应角相等，对应边成比例 . 7. 生活中的数学无处不在，只要你愿意去发现，其乐 无穷 . 课后作业 用适当的符号表示下列关系 （ 1 ） x 的 3 倍与 8 的和比 x 的 5 倍大； （ 2 ） x 2 是非负数； （ 3 ）地球上海洋面积大于陆地面积； （ 4 ）老师的年龄比你年龄的 2 倍还大； （ 5 ）铅球的质量比蓝球的质量大；