苏教版数学九年级上册教案2-4圆周角（2）

苏教版数学九年级上册教案2-4圆周角（2）

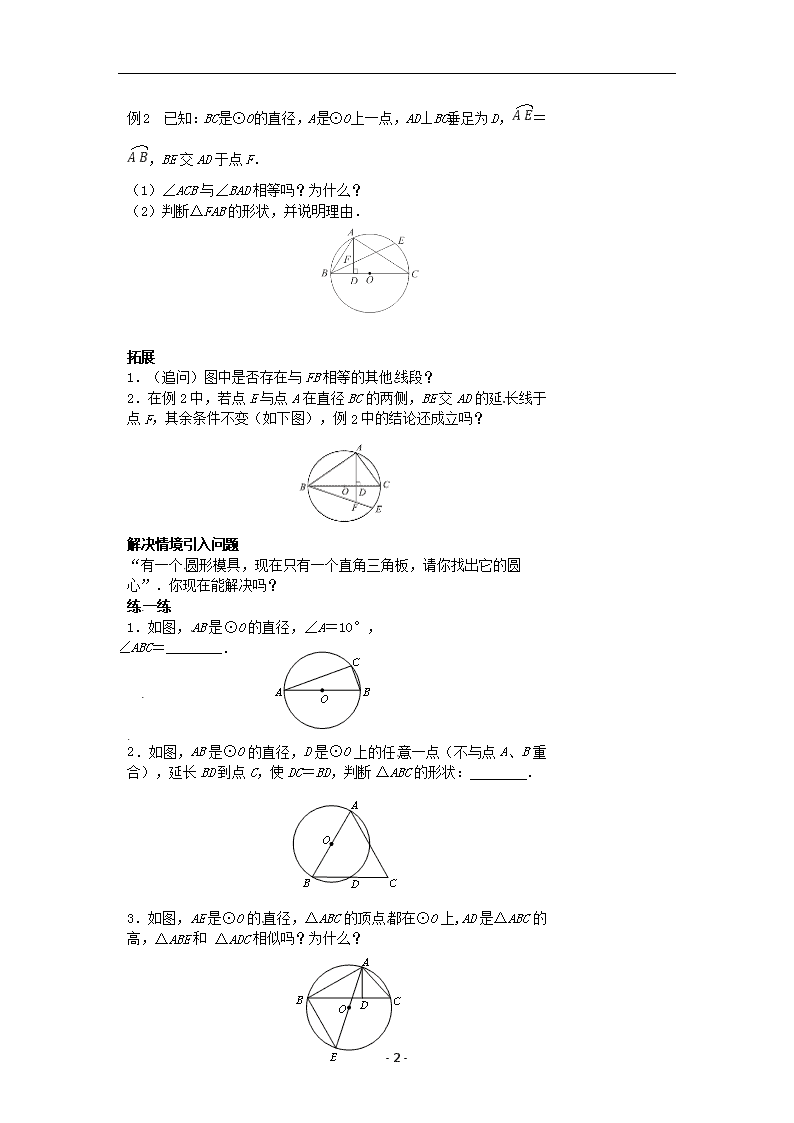
- 1 - 2.4 圆周角（2） 教学目标 【知识与能力】 进一步巩固圆周角的概念、圆周角定理，并能运用定理解决有关问题，掌握半圆（或直径） 所对的圆周角是直角；90°的圆周角所对的弦是直径. 【过程与方法】 经历圆周角性质的过程，培养学生分析问题和解决问题的能力 【情感态度价值观】 用联系的观点思考问题、转化问题. 教学重难点 【教学重点】 掌握直径和所对圆周角是直角之间的相互确定关系，灵活运用同弧所对的圆周角和圆心角的 关系解决问题. 【教学难点】 用联系的观点看问题中的条件，注重隐藏条件的发现. 课前准备 无 教学过程 情境引入 有一个圆形模具，现在只有一个直角三角板，请你找出它的圆心． 实践探索一 问题 1 如图 1，BC 是⊙O 的直径，A 是⊙O 上任一点，你能确定∠BAC 的度数吗? 问题 2 如图 2，圆周角∠BAC ＝90º，弦 BC 经过圆心 O 吗？为什么？ 请你对上面的结论进行归纳总结． 例题讲解 例 1 如图，AB 是⊙O 的直径，弦 CD 与 AB 相交于点 E，∠ACD＝60° ，∠ADC＝50°， 求∠CEB 的度数． - 2 - 例 2 已知：BC 是⊙O 的直径，A 是⊙O 上一点，AD⊥BC，垂足为 D， ⌒AE ＝⌒AB ，BE 交 AD 于点 F．[来源:学科网] （1）∠ACB 与∠BAD 相等吗？为什么？ （2）判断△FAB 的形状，并说明理由． 拓展 1．（追问）图中是否存在与 FB 相等的其他线段？ 2．在例 2 中，若点 E 与点 A 在直径 BC 的两侧，BE 交 AD 的延长线于 点 F，其余条件不变（如下图），例 2 中的结论还成立吗？ [来源:学+科+网 Z+X+X+K] 解决情境引入问题 “有一个圆形模具，现在只有一个直角三角板，请你找出它的圆心”．你 现在能解决吗？ 练一练 1．如图，AB 是⊙O 的直径，∠A＝10°， 则∠ABC＝________． 2．如图，AB 是⊙O 的直径，D 是⊙O 上的任 意一点（不与点 A、B 重 合），延长 BD 到点 C，使 DC＝BD，判断ΔABC 的形状： ． [来源:学科网 ZXXK] 3．如图，AE 是⊙O 的 直径，△ABC 的顶点 都在⊙O 上,AD 是△ABC 的 高，△ABE 和 △ADC 相似吗？为什么？ - 3 - 拓展提升 一个圆形人工湖，弦 AB 是湖上的一座桥，已知桥 AB 长 100m，测得圆 周角∠C＝45°，求这个人工湖的直径． [来源:学,科,网] 教师追问：你还有哪些方法？从中你得到什么启发？ 总结 这节课你有哪些收获和困惑？ 今天我们学习了圆中有哪些常用辅助线？