- 2021-11-10 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级下册数学教案29-5 正多边形和圆 冀教版
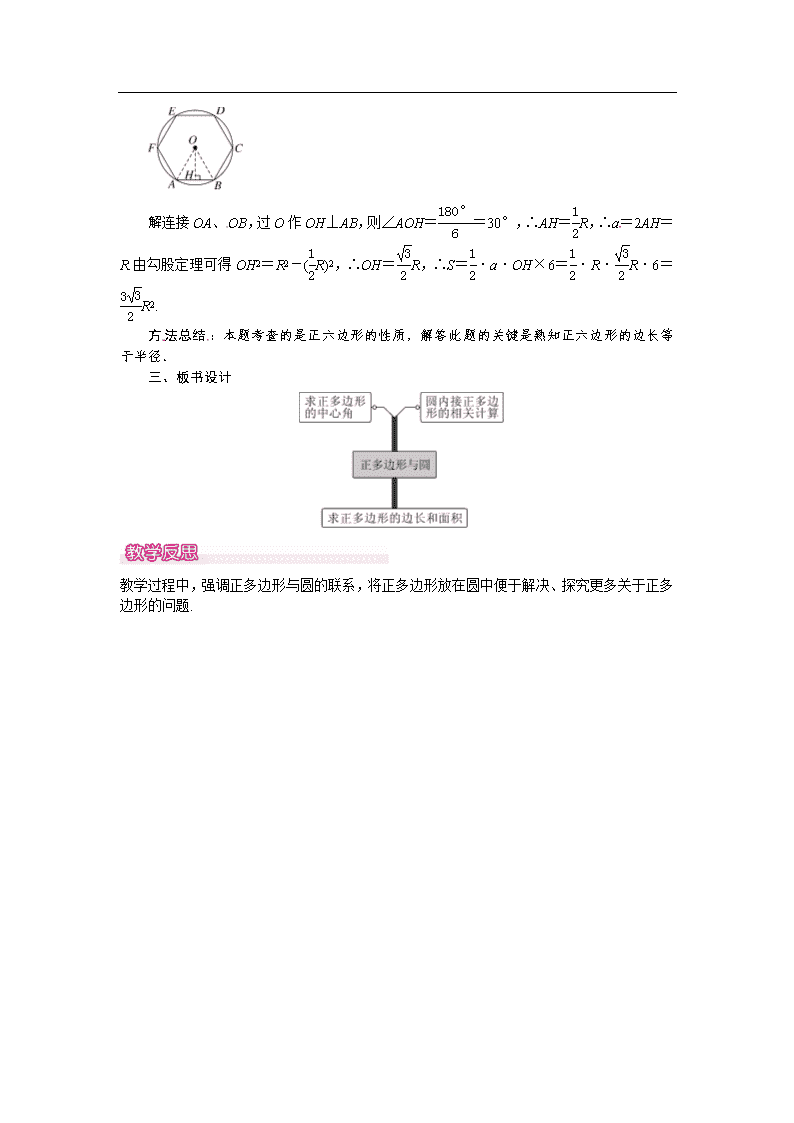
29.5 正多边形和圆 1.了解正多边形与圆的有关概念; 2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会运用正多边形和圆的有关知识画正多边形.(重点) 一、情境导入 生日宴会上,佳乐等6位同学一起过生日,他想把如图所示蛋糕平均分成6份,你能帮他做到吗?[来源:Zxxk.Com] 二、合作探究 探究点一:圆的内接正多边形的相关计算 如图,有一个圆O和两个正六边形T1,T2.T1的6个顶点都在圆周上,T2的6条边都和圆O相切.[来源:Z|xx|k.Com] (1)设T1,T2的边长分别为a,b,圆O的半径为r,求r∶a及r∶b的值; (2)求正六边形T1,T2的面积比S1∶S2的值. 解:(1)连接圆心O和T1的6个顶点可得6个全等的正三角形.所以r∶a=1∶1.连接圆心O和T2相邻的两个顶点,得以圆O的半径为高的正三角形,所以r∶b=∶2; (2)正六边形T1与T2的边长比是∶2,所以S1∶S2=3∶4. 方法总结:解答此题的关键是根据题意画出图形,再由三角函数的定义及特殊角的三角函数值求解.[来源:Z*xx*k.Com] 探究点二:与正多边形相关的计算 【类型一】 求正多边形的中心角 已知一个正多边形的每个内角均为108°,则它的中心角为________度. 解析:每个内角为108°,则每个外角为72°.根据多边形的外角和等于360°,∴正多边形的边数为5,则其中心角为360°÷5=72°.故填72. 方法总结:本题考查了正多边形的内角与外角,对于正多边形,利用多边形的外角和除以每一个外角的度数求边数更简便. 【类型二】 求正多边形的边长和面积 已知正六边形ABCDEF的外接圆半径是R,求正六边形的边长a和面积S.[来源:Z|xx|k.Com] 解:连接OA、OB,过O作OH⊥AB,则∠AOH==30°,∴AH=R,∴a=2AH=R.由勾股定理可得OH2=R2-(R)2,∴OH=R,∴S=·a·OH×6=·R·R·6=R2. 方法总结:本题考查的是正六边形的性质,解答此题的关键是熟知正六边形的边长等于半径. 三、板书设计 [来源:Zxxk.Com] 教学过程中,强调正多边形与圆的联系,将正多边形放在圆中便于解决、探究更多关于正多边形的问题.查看更多