平行线分线段成例教案2

平行线分线段成例教案2

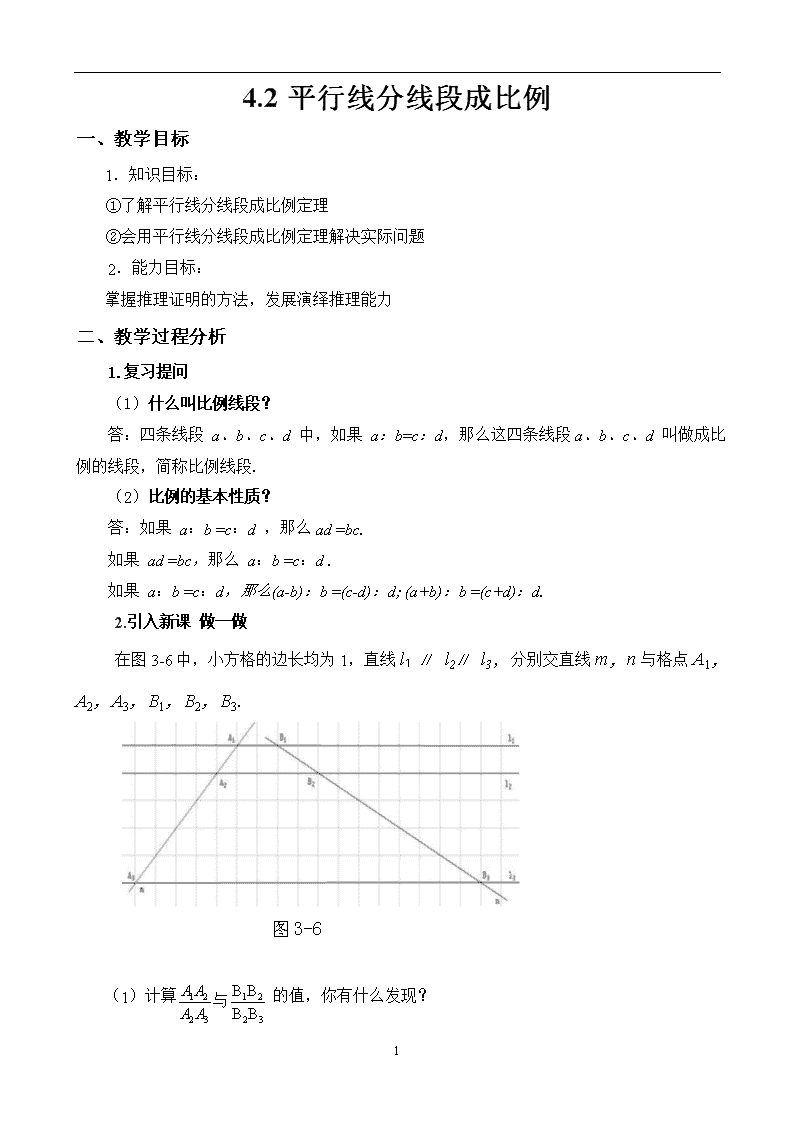
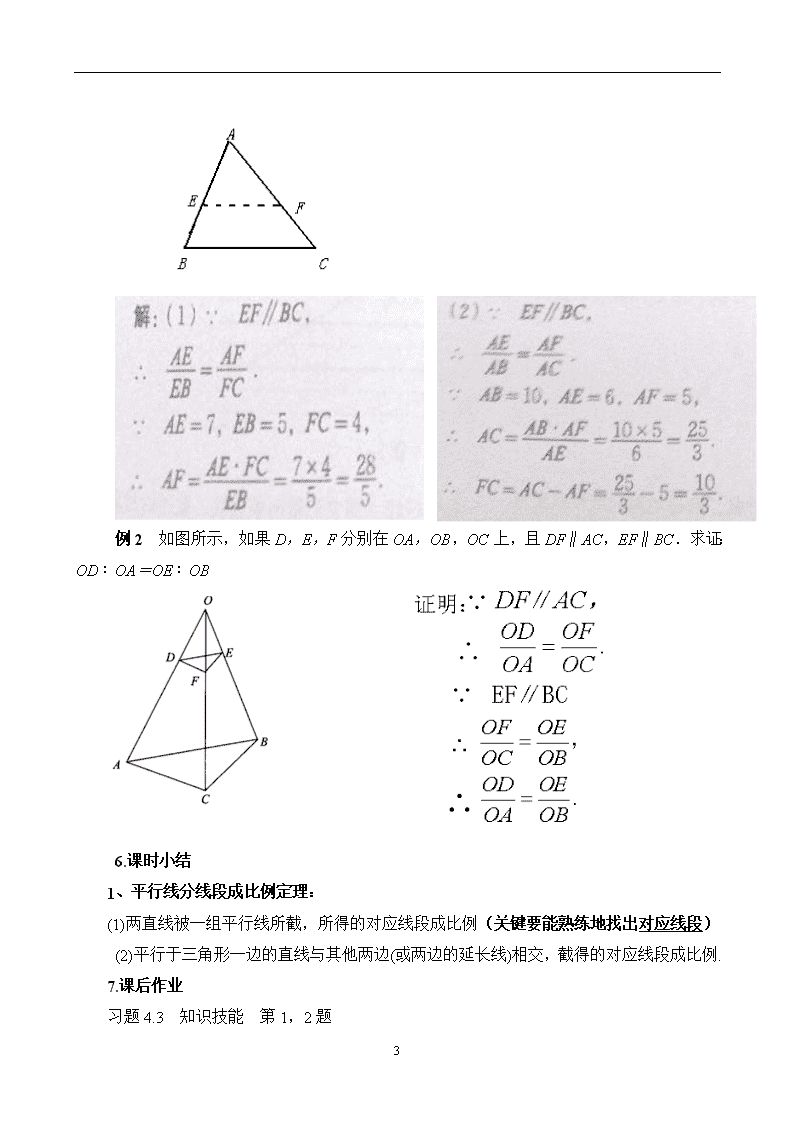
‎4.2平行线分线段成比例 一、教学目标 ‎1．知识目标：‎ ‎①了解平行线分线段成比例定理 ‎②会用平行线分线段成比例定理解决实际问题 ‎2．能力目标：‎ 掌握推理证明的方法，发展演绎推理能力 二、教学过程分析 ‎1.复习提问 ‎（1）什么叫比例线段？‎ 答：四条线段 a、b、c、d 中，如果 a：b=c：d，那么这四条线段a、b、c、d 叫做成比例的线段，简称比例线段.‎ ‎（2）比例的基本性质？‎ 答：如果 a：b =c：d ，那么ad =bc.‎ 如果 ad =bc，那么 a：b =c：d .‎ 如果 a：b =c：d，那么(a-b)：b =(c-d)：d; (a+b)：b =(c+d)：d.‎ ‎2.引入新课 做一做 在图3-6中，小方格的边长均为1，直线l1 ∥ l2∥ l3，分别交直线m，n与格点A1，A2，A3，B1，B2，B3.‎ 图3-6‎ ‎（1）计算 的值，你有什么发现？‎ 4‎ ‎ （2）将向下平移到如图3-7的位置，直线m,n 与的交点分别为 你在问题（1）中发现结论还成立吗？如果将平移到其它位置呢？‎ ‎（3）在平面上任意作三条平行线，用它们截两条直线，截得的线段成比例吗？‎ ‎3.分组讨论，得出结论 平行线分线段成比例定理：‎ 两条直线被一组平行线所截，所得的对应线段成比例.‎ ‎4.想一想 ‎（一）如果把图1中l1 , l2两条直线相交，交点A刚落到l3上，如图2所得的对应线段的比会相等吗？依据是什么？ ‎ ‎（二）如果把图1中l1, l2两条直线相交，交点A刚落到l4上，如图2（2）所得的对应线段的比会相等吗？依据是什么？ ‎ 得出结论：（推论）‎ ‎ 平行于三角形一边的直线与其他两边(或两边的延长线)相交，截得的对应线段成比例.‎ ‎5. 例题学习 例1 如图，在△ABC中，E，F分别是AB和AC上的点，且EF∥BC。‎ ‎（1）如果AE=7 ，EB=5，FC=4.那么AF的长是多少？‎ ‎（2）如果AB=10 ，AE=6，AF=5.那么FC的长是多少？‎ 4‎ 例2 如图所示，如果D，E，F分别在OA，OB，OC上，且DF∥AC，EF∥BC．求证：OD∶OA＝OE∶OB ‎ ‎6.课时小结 ‎1、平行线分线段成比例定理：‎ ‎(1)两直线被一组平行线所截，所得的对应线段成比例（关键要能熟练地找出对应线段）‎ ‎ (2)平行于三角形一边的直线与其他两边(或两边的延长线)相交，截得的对应线段成比例.‎ ‎7.课后作业 习题4.3 知识技能 第1，2题 4‎ 4‎