初中数学中考总复习课件PPT：第22课时　平行四边形与多边形

初中数学中考总复习课件PPT：第22课时　平行四边形与多边形

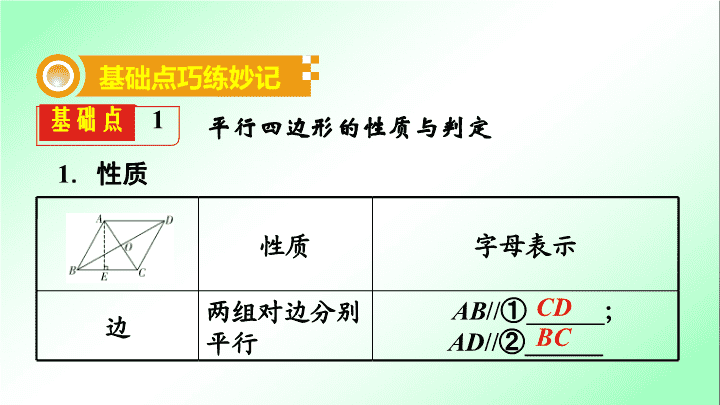
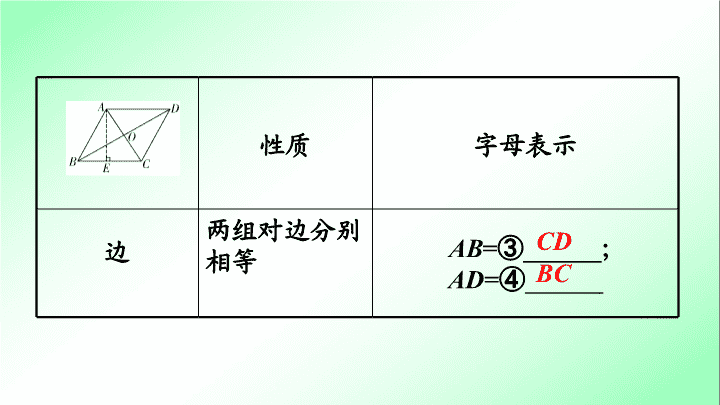
第一部分 夯实基础　提分多 第 五 单元 四边形 第 22 课时　平行四边形与多边形 1 ． 性质 基础点 1 平行四边形的性质与判定 性质 字母表示 边 两组对边分别平行 AB // ① ______ ； AD // ② ______ CD BC 基础点巧练妙记 性质 字母表示 两组对边分别相等 AB = ③ ______ ； AD = ④ ______ CD BC 边 性质 字母表示 角 两组对角分别⑤ ______ ∠ ABC = ⑥ ______ ； ∠ BAD = ⑦ ______ 邻角⑧ ______ ∠BAD ＋∠ ABC ＝ 180° ； ∠BAD ＋⑨ _______ ＝ 180° 相等 ∠ ADC ∠ BCD 互补 ∠ ADC 性质 字母表示 对角线 互相⑩ _______ OA = ⑪ _______ OB = ⑫ _______ 对称性 是中心对称图形，但不是轴对称图形 面积 S ▱ ABCD ＝ BC · AE ＝ AD · AE OC 平分 OD 2 ． 判定 文字描述 字母表示 边 有两组对边分别⑬ ______ 的四边形是平行四边形 AB // CD AD // ⑭ ______ 四边形 ABCD 是平行四边形 => 平行 BC 文字描述 字母表示 边 有两组对边分别⑮ ______ 的四边形是平行四边形 AB = CD AD = BC 四边形 ABCD 是平行四边形 => 相等 文字描述 字母表示 边 有一组对边⑯ __________ 的四边形是平行四边形 AB //CD AB = CD AD//BC AD=BC 四边形 ABCD 是平行四边形 或 平行且相等 => 文字描述 字母表示 角 两组对角分别⑰ ______ 的四边形是平行四边形 ∠ DAB = ∠ DCB ∠ ADC = ∠ ABC 四边形 ABCD 是平行四边形 相等 => 文字描述 字母表示 对角线 对角线⑱ _________ 的四边形是平行四边形 AO = CO BO = DO 四边形 ABCD 是平行四边形 互相平分 =>            7 失 分 点 平行四边形的判定条件运用错误 判断正误 1. 两组对边分别相等的四边形是平行四边形． ( 　　 ) 2. 一组对边平行，另一组对边相等的四边形是平行四边形． ( 　　 ) √ ×            7 失 分 点 3. 一条对角线平分另一条对角线的四边形是平行四边形． ( 　　 ) 4. 两组对边分别平行的四边形是平行四边形． ( 　　 ) 5. 任意四边形四边中点连线构成的四边形是平行四边形． ( 　　 ) × √ √ 【 名师提醒 】 运用判定定理“有一组对边平行且相等的四边形是平行四边形”时，注意是同一组对边平行且相等的四边形才是平行四边形．            练 提 分 必 1 ．在四边形 ABCD 中， AD ∥ BC ，要判别四边形 ABCD 是平行四边形，还需满足条件 ( 　　 ) A ．∠ A ＋∠ C ＝ 180 ° 　　 B ．∠ B ＋∠ D ＝ 180 ° C ．∠ B ＋∠ A ＝ 180 ° D ．∠ A ＋∠ D ＝ 180 ° D            练 提 分 必 2 ．已知在四边形 ABCD 中， AB ∥ CD ， AB ＝ CD ，周长为 40cm ，两邻边的比是 3∶2 ，则较大边的长度是 ( 　　 ) A ． 8cm 　 　 B ． 10cm 　　 C ． 12cm D ． 14cm C            练 提 分 必 3 ．如图，在平行四边形 ABCD 中， E 是 AB 延长线上的一点，若∠ A ＝ 60 ° ，则∠ 1 的度数为 ( 　　 ) A ． 30 ° 　　 B ． 60 ° 　　 C ． 120 ° 　　 D ． 90 ° B 第 3 题图 n 边形 （ n ≥ 3 ） 内角和定理 n 边形的内角和为⑲ ____________ 外角和定理 n 边形的外角和为⑳ _________ 对角线 过 n （ n ＞ 3 ）边形一个顶点可引 ________ 条对角线， n 边形共有 条对角线 基础点 2 多边形及其性质 ( n － 2)•180 ° 360 ° n- 3 21 正 n 边形 （ n ≥ 3 ） 性质 （ 1 ）正 n 边形的各边相等，各角相等； （ 2 ）正 n 边形的每一个内角为 ，每一个外角为 ； （ 3 ）对于正 n 边形，当 n 为奇数时，是轴对称图形，不是中心对称图形；当 n 为偶数时，既是轴对称图形，又是中心对称图形 重难点精讲优练 类型 平行四边形的相关证明与计算 例 　如图，四边形 ABCD 中， AE ⊥ BD 于点 E ， CF ⊥ BD 于点 F ， AE ＝ CF ， BE ＝ DF . 求证： (1)△ ABE ≌△ CDF ； 【 思维教练 】 要证△ ABE ≌ △ CDF ，由已知条件结合全等三角形的判定方法 SAS 即可求证； 例题图 例题图 证明 ： (1)∵ AE ⊥ BD ， CF ⊥ BD ， ∴∠ AEB ＝∠ CFD ＝ 90° ， ∵ AE ＝ CF ， BE ＝ DF ， ∴△ ABE ≌ △ CDF ( SAS ) ； (2) 四边形 ABCD 是平行四边形． 【 思维教练 】 要证四边形 ABCD 是平行四边形，结合 (1) 易得 AB ＝ CD ，再由∠ ABE ＝∠ CDF ( 内错角相等 ) ，推出一组对边 AB ∥ CD ，即可得证． 例题图 例题图 (2) 证明： ∵△ ABE ≌ △ CDF ， ∴ AB ＝ CD ，∠ ABE ＝∠ CDF ， ∴ AB ∥ CD ， ∴四边形 ABCD 是平行四边形． 练习 1 　 (2017 黑龙江 ) 在平行四边形 ABCD 中，∠ A 的平分线把 BC 边分成长度是 3 和 4 的两部分，则平行四边形 ABCD 的周长是 ( 　　 ) A. 22 B. 20 C. 22 或 20 　 D. 18 C 练习 1 题解图 【 解析 】 在平行四边形 ABCD 中， AD ∥ BC ，则∠ DAE ＝∠ AEB ，∵ AE 平分∠ BAD ，∴∠ BAE ＝∠ DAE ，∴∠ BAE ＝∠ BEA ，∴ AB ＝ BE ， BC ＝ BE ＋ EC ，①当 BE ＝ 3 ， EC ＝ 4 时，平行四边形 ABCD 的周长为： 2( AB ＋ BC ) ＝ 2(3 ＋ 3 ＋ 4) ＝ 20 ；②当 BE ＝ 4 ， EC ＝ 3 时，平行四边形 ABCD 的周长为： 2( AB ＋ BC ) ＝ 2(4 ＋ 4 ＋ 3) ＝ 22. 练习 2 　 如图，四边形 ABCD 为平行四边形，∠ BAD 的角平分线 AE 交 CD 于点 F ，交 BC 的延长线于点 E . (1) 求证： BE ＝ CD ； 练习 2 题图 证明 ：∵四边形 ABCD 是平行四边形， ∴ AD ∥ BE ， AB ＝ CD ， ∴∠ DAE ＝∠ AEB ， ∵ AE 平分∠ BAD ， ∴∠ BAE ＝∠ DAE ， ∴∠ BAE ＝∠ AEB ， ∴ AB ＝ BE ，∴ BE ＝ CD ； (2) 连接 BF ，若 BF ⊥ AE ，∠ BEA ＝ 60 ° ， AB ＝ 4 ，求平行四边形 ABCD 的面积． 解：由（ 1 ）知 AB=BE ， ∵∠ BEA =60 ° ∴ AB=BE=AE =4 ， ∵ BF ⊥ AE ， ∴ AF=EF ， BF=AB ·sin60 ° =4 × = ， ∴ S △ ABE = AE·BF = ， ∵ AD//BE ， ∴∠ D= ∠ ECF ， 在△ ADF 和△ ECF 中， ∠ D =∠ ECF ∠ AFD =∠ EFC ， ∴ △ ADF ≌ △ ECF （ AAS ）， AF=EF ∴ S △ ADF = S △ ECF ， ∴ S ABCD =S △ ABE = .            导 方 法 指 1. 判定平行四边形： (1) 若已知一组对边相等，则需证这组对边平行或者另外一组对边相等； (2) 若已知一组对边平行，则需证明这组对边相等或者另外一组对边平行； (3) 若已知一组对角相等，则需证另一组对角相等； (4) 若已知一条对角线平分另一条对角线，则需证对角线互相平分．            导 方 法 指 2. 证明线段、角相等： (1) 证明线段或角所在的两个三角形全等； (2) 结合平行四边形性质证明三角形为等腰三角形，从而证得线段、角相等．