中心对称　　导学案3

中心对称　　导学案3

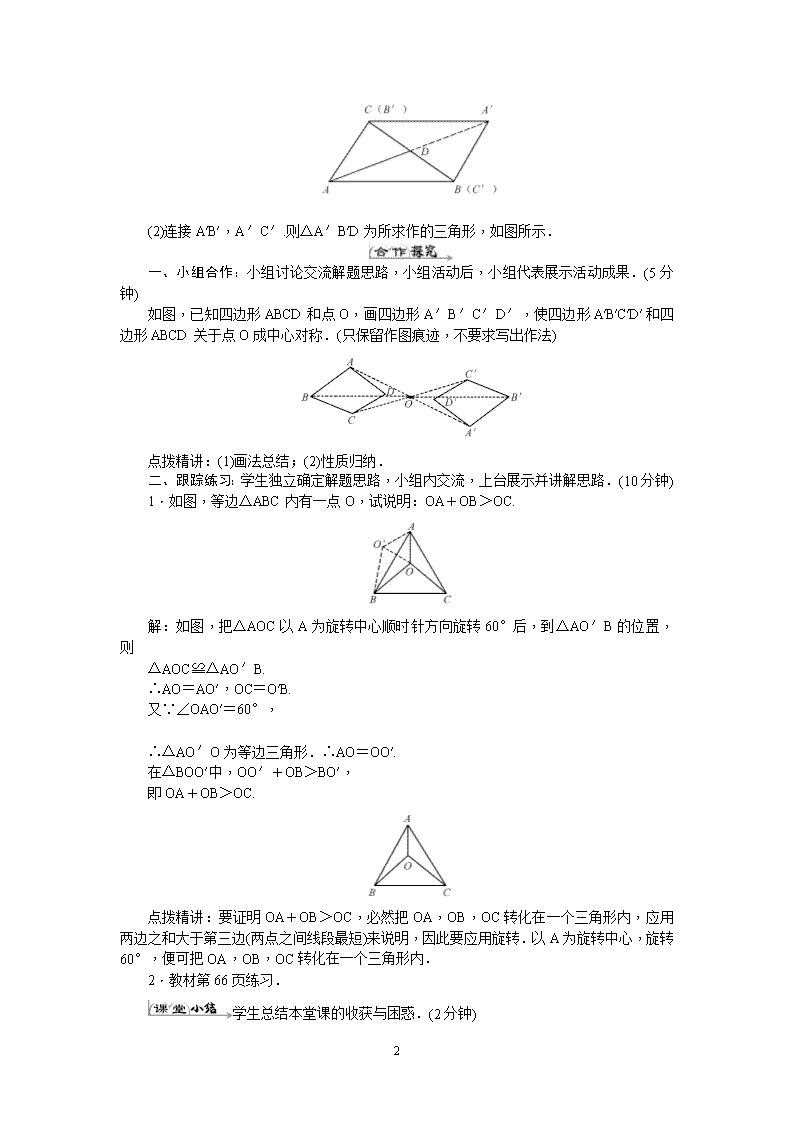
1 23..2. 1 中心对称 1. 了解中心对称、对称中心、关于中心的对称点等概念． 2. 掌握中心对称的基本性质． 重点：中心对称的性质及初步应用． 难点：中心对称与旋转之间的关系． 一、自学指导．(10 分钟) 自学 1：中心对称，对称中心，对称点等概念：把一个图形绕某一个点旋转 180°，如 果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称(central symmetry)；这个点叫做对称中心；这两个图形中的对应点叫做关于对称中心的对称点． 自学 2：中心对称的性质： (1)关于中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平 分； (2)关于中心对称的两个图形是全等图形． 二、自学检测：学生自主完成，小组内展示，点评，教师巡视．(8 分钟) 1．如图，四边形 ABCD 绕 D 点旋转 180°，请作出旋转后的图案，写出作法并回答． (1)这两个图形是中心对称图形吗？如果是，对称中心是哪一点？如果不是，请说明理 由． (2)如果是中心对称，那么 A，B，C，D 关于中心对称的对称点是哪些点． 解：(1)根据中心对称的定义便知这两个图形是中心对称图形，对称中心是 D 点． (2)A，B，C，D 关于中心 D 的对称点是 A′，B′，C′，D′，这里的 D′与 D 重合． 2．如图，已知 AD 是△ABC 的中线，作出以点 D 为对称中心， 与△ABD 成中心对称的三角形． 分析：因为 D 是对称中心且 AD 是△ABC 的中线，所以 C，B 为一对对应点，因此， 只要再作出 A 关于 D 的对应点即可． 解：(1)延长 AD，且使 AD＝DA′，因为 C 点关于 D 的中心对称点是 B(C′)，A 点关于中 心 D 的对称点为 A′. 2 (2)连接 A′B′，A′C′.则△A′B′D 为所求作的三角形，如图所示． 一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(5 分 钟) 如图，已知四边形 ABCD 和点 O，画四边形 A′B′C′D′，使四边形 A′B′C′D′和四 边形 ABCD 关于点 O 成中心对称．(只保留作图痕迹，不要求写出作法) 点拨精讲：(1)画法总结；(2)性质归纳． 二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路．(10 分钟) 1．如图，等边△ABC 内有一点 O，试说明：OA＋OB＞OC. 解：如图，把△AOC 以 A 为旋转中心顺时针方向旋转 60°后，到△AO′B 的位置， 则 △AOC≌△AO′B. ∴AO＝AO′，OC＝O′B. 又∵∠OAO′＝60°， ∴△AO′O 为等边三角形．∴AO＝OO′. 在△BOO′中，OO′＋OB＞BO′， 即 OA＋OB＞OC. 点拨精讲：要证明 OA＋OB＞OC，必然把 OA，OB，OC 转化在一个三角形内，应用 两边之和大于第三边(两点之间线段最短)来说明，因此要应用旋转．以 A 为旋转中心，旋转 60°，便可把 OA，OB，OC 转化在一个三角形内． 2．教材第 66 页练习． 学生总结本堂课的收获与困惑．(2 分钟) 3 1．中心对称及对称中心的概念； 2．关于中心对称的两个图形的性质． 学习至此，请使用本课时对应训练部分．(10 分钟)