关于原点对称的点的坐标　　导学案2

关于原点对称的点的坐标　　导学案2

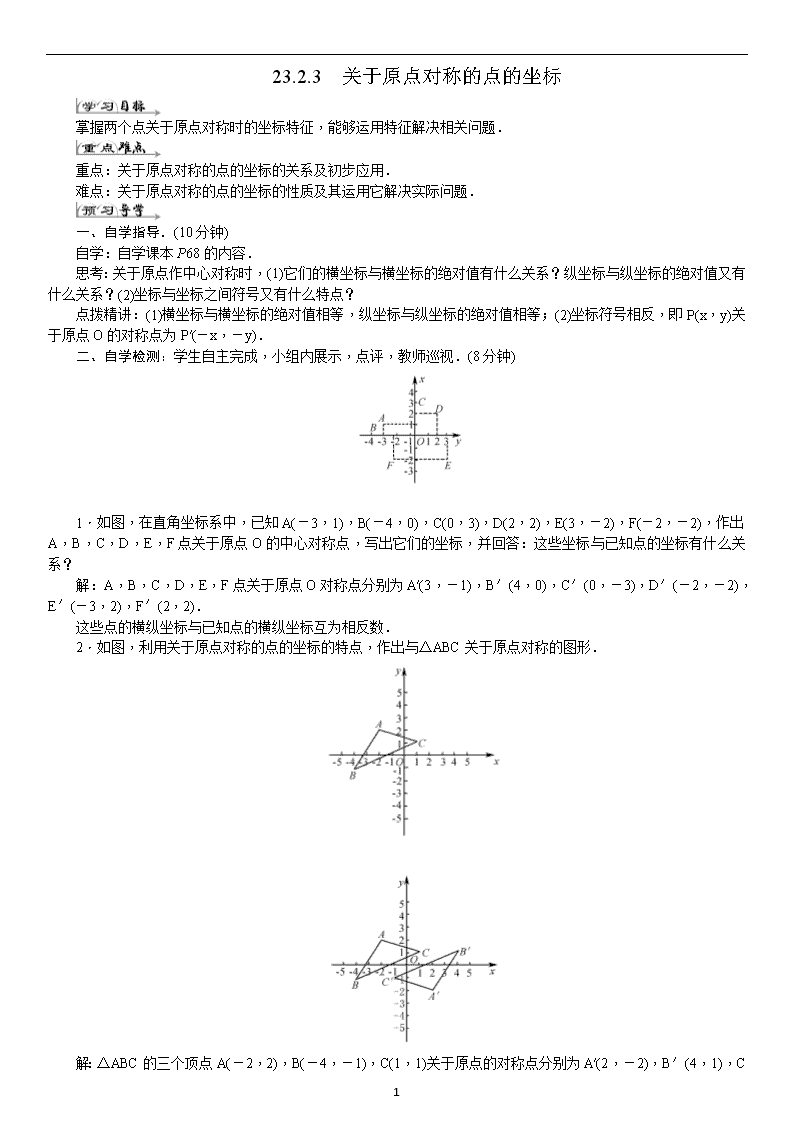
‎23.2.3　关于原点对称的点的坐标 掌握两个点关于原点对称时的坐标特征，能够运用特征解决相关问题．‎ 重点：关于原点对称的点的坐标的关系及初步应用．‎ 难点：关于原点对称的点的坐标的性质及其运用它解决实际问题．‎ 一、自学指导．(10分钟)‎ 自学：自学课本P68的内容．‎ 思考：关于原点作中心对称时，(1)它们的横坐标与横坐标的绝对值有什么关系？纵坐标与纵坐标的绝对值又有什么关系？(2)坐标与坐标之间符号又有什么特点？‎ 点拨精讲：(1)横坐标与横坐标的绝对值相等，纵坐标与纵坐标的绝对值相等；(2)坐标符号相反，即P(x，y)关于原点O的对称点为P′(－x，－y)．‎ 二、自学检测：学生自主完成，小组内展示，点评，教师巡视．(8分钟)‎ ‎1．如图，在直角坐标系中，已知A(－3，1)，B(－4，0)，C(0，3)，D(2，2)，E(3，－2)，F(－2，－2)，作出A，B，C，D，E，F点关于原点O的中心对称点，写出它们的坐标，并回答：这些坐标与已知点的坐标有什么关系？‎ 解：A，B，C，D，E，F点关于原点O对称点分别为A′(3，－1)，B′(4，0)，C′(0，－3)，D′(－2，－2)，E′(－3，2)，F′(2，2)．‎ 这些点的横纵坐标与已知点的横纵坐标互为相反数．‎ ‎2．如图，利用关于原点对称的点的坐标的特点，作出与△ABC关于原点对称的图形．‎ 解：△ABC的三个顶点A(－2，2)，B(－4，－1)，C(1，1)关于原点的对称点分别为A′(2，－2)，B′(4，1)，C 2‎ ‎′(－1，－1)，依次连接A′B′，B′C′，A′C′，就可得到与△ABC关于原点对称的△A′B′C′，如右图所示．‎ 一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(8分钟)‎ 如图，直线AB与x轴、y轴分别相交于A，B两点，将直线AB绕点O顺时针旋转90°得到直线A1B1.‎ ‎(1)在图中画出直线A1B1.‎ ‎(2)求出过线段A1B1中点的反比例函数解析式．‎ ‎(3)是否存在另一条与直线A1B1平行的直线y＝kx＋b(我们发现互相平行的两条直线斜率k值相等)，它与双曲线只有一个交点，若存在，求此直线的函数解析式，若不存在，请说明理由．‎ 点拨精讲：(1)只需画出A，B两点绕点O顺时针旋转90°得到的点A1，B1，连接A1B1.‎ ‎(2)先求出A1B1中点的坐标，设反比例函数解析式为y＝代入求k.‎ ‎(3)要回答是否存在，如果你判断存在，只需找出即可；如果不存在，才加以说明．这一条直线是存在的，因为A1B1与双曲线是相切的，只要我们通过A1B1的坐标作A1，B1关于原点的对称点A2，B2，连接 A2B2的直线就是我们所求的直线．‎ 二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路．(7分钟)‎ ‎1．已知△ABC，A(1，2)，B(－1，3)，C(－2，4)，利用关于原点对称的点的坐标的特点，作出△ABC关于原点对称的图形．‎ 点拨精讲：先在直角坐标系中画出A，B，C三点并连接组成△ABC，要作出△ABC关于原点O的对称三角形，只需作出△ABC中的A，B，C三点关于原点的对称点，依次连接，便可得到所求作的△A′B′C′.‎ ‎2．教材P69的第1，2，3题．‎ 学生总结本堂课的收获与困惑．(2分钟)‎ 本节课应掌握：两个点关于原点对称时，它们的坐标符号相反，即点P(x，y)关于原点的对称点P′(－x，－y)，及利用这些特点解决一些实际问题．‎ 学习至此，请使用本课时对应训练部分．(10分钟)‎ 2‎