二次函数导学案(3)二次函数 y＝ax2＋k的图象与性质

二次函数导学案(3)二次函数 y＝ax2＋k的图象与性质

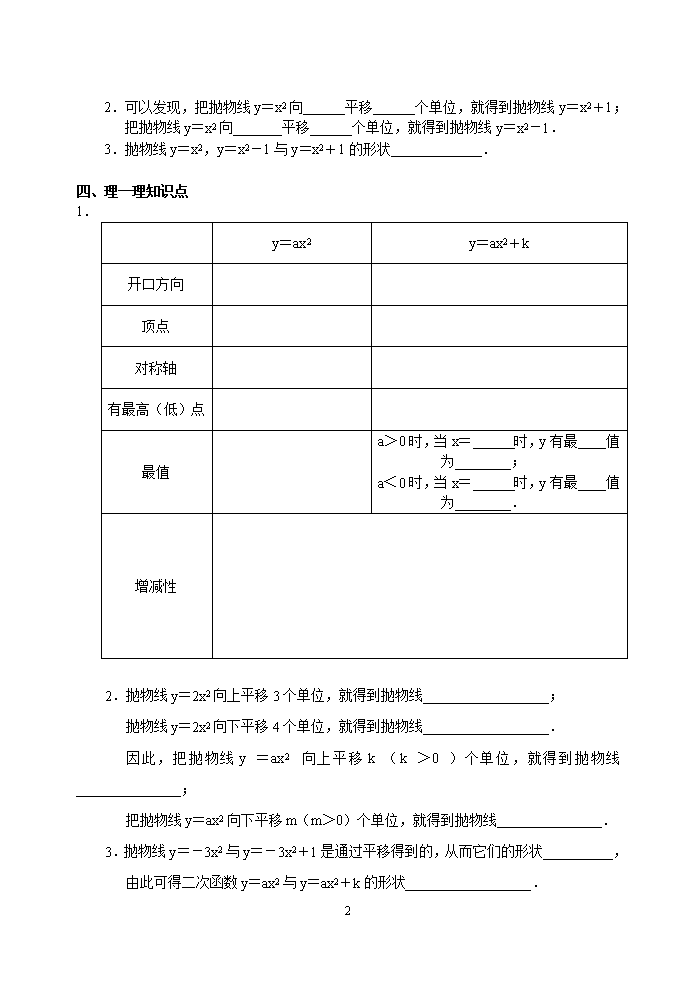
第二十二章 二次函数 第3课时 二次函数y＝ax2＋k的图象与性质 一、阅读课本： ‎ 二、学习目标：‎ ‎1．会画二次函数y＝ax2＋k的图象；‎ ‎2．掌握二次函数y＝ax2＋k的性质，并会应用；‎ ‎3．知道二次函数y＝ax2与y＝的ax2＋k的联系．‎ 三、探索新知：‎ 在同一直角坐标系中，画出二次函数y＝x2＋1，y＝x2－1的图象．‎ 解：先列表 x ‎…‎ ‎－3‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ y＝x2＋1‎ ‎…‎ ‎…‎ y＝x2－1‎ ‎…‎ ‎…‎ 描点并画图 观察图象得：‎ ‎1．‎ 开口方向 顶点 对称轴 有最高（低）点 最值 y＝x2‎ y＝x2－1‎ y＝x2＋1‎ 3‎ ‎2．可以发现，把抛物线y＝x2向______平移______个单位，就得到抛物线y＝x2＋1；把抛物线y＝x2向_______平移______个单位，就得到抛物线y＝x2－1．‎ ‎3．抛物线y＝x2，y＝x2－1与y＝x2＋1的形状_____________．‎ 四、理一理知识点 ‎1．‎ y＝ax2‎ y＝ax2＋k 开口方向 顶点 对称轴 有最高（低）点 最值 a＞0时，当x＝______时，y有最____值为________；‎ a＜0时，当x＝______时，y有最____值为________．‎ 增减性 ‎2．抛物线y＝2x2向上平移3个单位，就得到抛物线__________________；‎ ‎ 抛物线y＝2x2向下平移4个单位，就得到抛物线__________________．‎ ‎ 因此，把抛物线y＝ax2向上平移k（k＞0）个单位，就得到抛物线_______________；‎ ‎ 把抛物线y＝ax2向下平移m（m＞0）个单位，就得到抛物线_______________．‎ ‎3．抛物线y＝－3x2与y＝－3x2＋1是通过平移得到的，从而它们的形状__________，由此可得二次函数y＝ax2与y＝ax2＋k的形状__________________．‎ 3‎ 五、课堂巩固训练 ‎1．填表 函数 草图 开口方向 顶点 对称轴 最值 对称轴右侧的增减性 y＝3x2‎ y＝－3x2＋1‎ y＝－4x2－5‎ ‎2．将二次函数y＝5x2－3向上平移7个单位后所得到的抛物线解析式为_________________．‎ ‎3．写出一个顶点坐标为（0，－3），开口方向与抛物线y＝－x2的方向相反，形状相同的抛 物线解析式____________________________．‎ ‎4．抛物线y＝4x2＋1关于x轴对称的抛物线解析式为______________________．‎ 六、目标检测 ‎1．填表 函数 开口方向 顶点 对称轴 最值 对称轴左侧的增减性 y＝－5x2＋3‎ y＝7x2－1‎ ‎2．抛物线y＝－x2－2可由抛物线y＝－x2＋3向___________平移_________个单位得到的．‎ ‎3．抛物线y＝－x2＋h的顶点坐标为（0，2），则h＝_______________．‎ ‎4．抛物线y＝4x2－1与y轴的交点坐标为_____________，与x轴的交点坐标为_________．‎ 3‎ 3‎