江苏省无锡市九年级9月份月考数学试题

江苏省无锡市九年级9月份月考数学试题

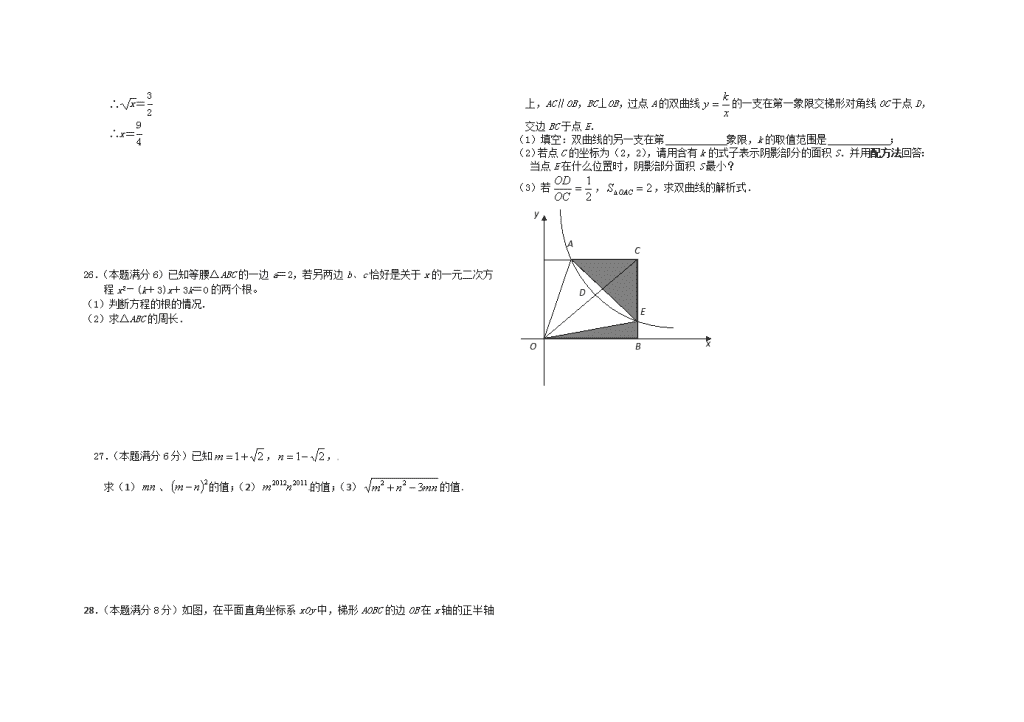
九年级数学阶段检测 9 月份月考试题 一．选择题（本大题共有 8 小题，每小题 3 分，共 24 分．） 1.若代数式 3x 有意义，则 x 的取值范围为 （ ） A. 3x B. 3x C. 3x D. 3x 2.下列运算中，正确的是 （ ） A. 24  B. 1025  C. 5)5( 2  D. 725  3. 用 配 方 法 解 方 程 0142  xx 时 ， 配 方 后 所 得 的 方 程 是 （ ） A. 1)2( 2 x B . 1)2( 2 x C. 3)2( 2 x D. 3)2( 2 x 4.下列一元二次方程中，两实数根之和为 5 的方程是 （ ） A. 0572  xx B. 0352  xx C. 0852  xx D. 0252  xx 5. 方 程 2 23 2mx x x mx    是 关 于 x 的 一 元 二 次 方 程 ， 则 m 的 取 值 范 围 为 （ ） A. 1m B. 0m C. 1m D. 1m 6. 关 于 x 的 方 程 kx2+3x-1=0 有 实 数 根 ， 则 k 的 取 值 范 围 是 ( ) A. 4 9k B. 4 9k 且 k≠0 C. 4 9k D. 4 9k 且 k≠0 7. 已 知 关 于 x 的 方 程 x 2 ＋ bx ＋ a ＝ 0 有 一 个 根 是 － a(a≠0) ， 则 a － b 的 值 为 （ ） A．－１ B．0 C．1 D．2 8.关于 x 的方程 a(x＋m)2＋b＝0 的解是 x1＝－2，x2＝1（a，m，b 均为常数，a≠0），则方 程 a(x＋m＋2)2＋b＝0 的解是 （ ） A．－2 或 1 B．－4 或－1 C．1 或 3 D．无法求解 二．填空题（本大题共有 8 小题，每空 2 分，共 22 分．） 9．一元二次方程    4213  xx 化成一般形式是 . 10.若 92  yx 与 3 yx 互为相反数，则 x＋y 的值 . 11.当 2＜x＜3 时，    2 22 3x x    _________, 当 x＜0 时，｜ x2 －x｜ =_________ 12.在实数范围内分解因式：2a2－4＝ . 13.若 4 122  kxx 是一个完全平方式，则 k = . 14.方程 1)1)(32(  xx 的解的情况是 . 15.若-2 是关于 x 的一元二次方程（k2-1）x2+2kx+4=0 的一个根，则 k=________． 16. 若 关 于 x 的 方 程 kx2 － 2x － 1 ＝ 0 有 两 个 不 相 等 的 实 数 根 ， 则 k 的 取 值 范 围 是 ． 17．学校组织一次乒乓球赛, 要求每两队之间都要赛一场. 若共赛了 15 场，则有几个球 队参赛?设有 x 个球队参赛，列出正确的方程___________________. 18．设 S1＝1＋1 12＋1 22，S2＝1＋1 22＋1 32，S3＝1＋1 32＋1 42,…， Sn＝1＋1 n2＋ 1 (n＋1)2. 设 S＝ S1＋ S2＋…＋ Sn，则 S＝_________ (用含 n 的代数式表示，其中 n 为正整数) 三．解答题（共有 10 小题，共 84 分．解答需写出必要的文字说明，演算步骤或证明过程．） 19．计算（每小题 4 分，共 16 分）： （1） 483912  （2） 5 12 2 1832 143 5  密 封 线 内 不 要 答 题 学 校 班 级 初 三 （ ） 姓 名 学 号 （3）  0,022 2  bab abbaa ba （4） 123 2324273 1        20．解下列方程（每小题 4 分，共 16 分）： ⑴ 3x2＝12x ⑵ 2y2－5y＋1＝0 ⑶1 4 x2－x－4＝0（用配方法） ⑷(x－1)2＋4(x－1)＋4＝0 21. （本题满分 8 分）已知 a 是一元二次方程 x2－4x＋1＝0 的两个实数根中较小的根， ⑴ 求 a2－4a＋2012 的值； ⑵ 化简求值1－2a＋a2 a－1 － a2－2a＋1 a2－a －1 a . 22.（本题满分 6 分）已知 x＝－1 是方程 x2＋mx－5＝0 的一个根，求 m 的值及方程的另 一个根. 23．（本题满分 6 分）已知关于 x 的一元二次方程 0142  mxx 有两个相等的实数 根，求 m 的值及方程的根. 24．（本题满分 6 分）当 k 取何值时，方程 0131323 22  kxkx ）（ （1）有一根为零. （2）有两个互为相反数的根. （3）两根互为倒数. 25.（本题满分 6 分）解方程时，把某个式子看成整体，用新的未知数去代替它，使方 程得到简化，这叫换元法．先阅读下面的解题过程，再解出右面的方程： 例：解方程：2 x－3＝0 请利用左面的方法，解方程 x＋2 x－8＝0 解：设 x＝t （t≥0） 解： ∴原方程化为 2t－3＝0 ∴t＝3 2 而 t＝3 2 ＞0 ∴ x＝3 2 ∴x＝9 4 26．（本题满分 6）已知等腰△ABC 的一边 a＝2，若另两边 b、c 恰好是关于 x 的一元二次方 程 x2－(k＋3)x＋3k＝0 的两个根。 （1）判断方程的根的情况. （2）求△ABC 的周长． 27．（本题满分 6 分）已知 21m ， 21n ， 求（1） mn 、 2nm  的值；（2） 20112012nm 的值；（3） mnnm 322  的值. 28．（本题满分 8 分）如图，在平面直角坐标系 xOy 中，梯形 AOBC 的边 OB 在 x 轴的正半轴 上，AC∥OB，BC⊥OB，过点 A 的双曲线 x ky  的一支在第一象限交梯形对角线 OC 于点 D， 交边 BC 于点 E． （1）填空：双曲线的另一支在第 象限，k 的取值范围是 ； （2）若点 C 的坐标为（2，2），请用含有 k 的式子表示阴影部分的面积 S．并用配方法回答： 当点 E 在什么位置时，阴影部分面积 S 最小？ （3）若 2 1 OC OD ， 2OACS ，求双曲线的解析式． C E BO D A y x