【精品试卷】中考数学一轮复习 专题测试-14 反比例函数（基础）（教师版）

【精品试卷】中考数学一轮复习 专题测试-14 反比例函数（基础）（教师版）

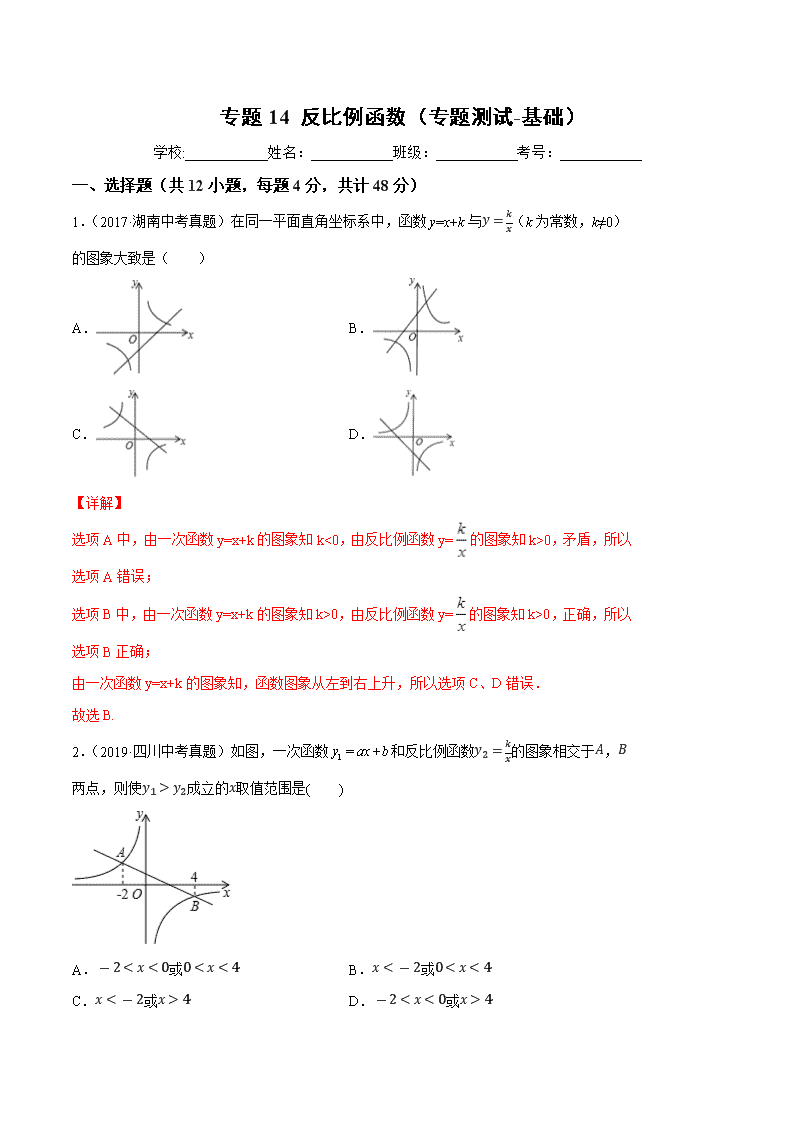
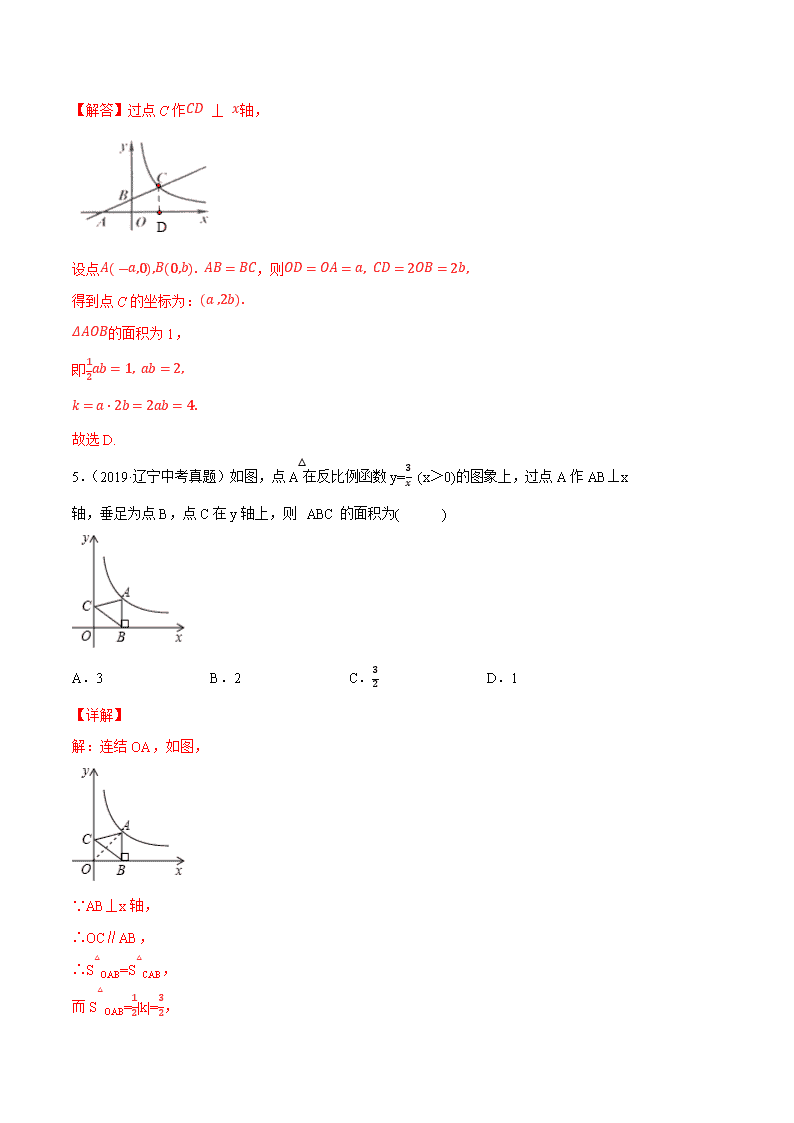
专题 14 反比例函数（专题测试-基础） 学校:___________姓名：___________班级：___________考号：___________ 一、选择题（共 12 小题，每题 4 分，共计 48 分） 1．（2017·湖南中考真题）在同一平面直角坐标系中，函数 y=x+k 与 N （k 为常数，k≠0） 的图象大致是（ ） A． B． C． D． 【详解】 选项 A 中，由一次函数 y=x+k 的图象知 k<0，由反比例函数 y= 的图象知 k>0，矛盾，所以 选项 A 错误； 选项 B 中，由一次函数 y=x+k 的图象知 k>0，由反比例函数 y= 的图象知 k>0，正确，所以 选项 B 正确； 由一次函数 y=x+k 的图象知，函数图象从左到右上升，所以选项 C、D 错误． 故选 B. 2．（2019·四川中考真题）如图，一次函数 1y ax b= + 和反比例函数 N 的图象相交于 ， 两点，则使 成立的 取值范围是( ) A． 䂄 䂄 或 䂄 䂄 B． 䂄 或 䂄 䂄 C． 䂄 或 D． 䂄 䂄 或 A．1 B．2 C．3 D．4 AOB 的面积为 1，则 k 的值为（ ） △ x 轴，y 轴分别交于点 A，B，且 AB=BC， （x>0）的图象上，过点 C 的直线与 4．（2018·浙江中考真题）如图，点 C 在反比例函数 y= 故选：C． . 䂄 䂄 或 䂄 的解集是 ݔ ∴不等式 ， 䂄 䂄 或 䂄 的取值范围是： ）的图象上方时， 且 为常数 （ N 的图象在反比例函数 N ݔ 解：由函数图象可知，当一次函数 【详解】 或 䂄 䂄 D． 䂄 䂄 或 䂄 䂄 䂄 C． B． 䂄 A． 是（ ） 的解集 ݔ ，结合图象，则不等式 䁠 䁠 䁠 ）的图象都经过 为常数且  （ my x 的图象与反比例函数 2 N ݔ ൅ 3．（2019·湖南中考真题）如图，一次函数 故选 B． ， 䂄 䂄 或 䂄 取值范围是 成立的 ∴使 时，一次函数图象在反比例函数图象上方， 䂄 䂄 或 䂄 观察函数图象可发现： 详解】】 【解答】过点 C 作 轴， 设点 쳌䁠 䁠 䁠 N ，则 N N 쳌䁠 N N 䁠得到点 C 的坐标为： 쳌䁠 的面积为 1， 即 쳌 N 䁠 쳌 N 䁠 N 쳌 N 쳌 N 故选 D. 5．（2019·辽宁中考真题）如图，点 A 在反比例函数 y= (x＞0)的图象上，过点 A 作 AB⊥x 轴，垂足为点 B，点 C 在 y 轴上，则 △ ABC 的面积为( ) A．3 B．2 C． D．1 【详解】 解：连结 OA，如图， ∵AB⊥x 轴， ∴OC∥AB， ∴S △ OAB=S △ CAB， 而 S △ OAB= |k|= ， ∴S △ CAB= ， 故选：C． 6．（2019·山东中考真题）如图，直线 l 与 x 轴，y 轴分别交于 A，B 两点，且与反比例函数 y＝ （x＞0）的图象交于点 C，若 S △ AOB＝S △ BOC＝1，则 k＝（ ） A．1 B．2 C．3 D．4 【详解】 如图，作 CD⊥x 轴于 D，设 OB＝a（a＞0）． ∵S △ AOB＝S △ BOC， ∴AB＝BC． ∵△AOB 的面积为 1， ∴ OA•OB＝1， ∴OA＝ 쳌 ， ∵CD∥OB，AB＝BC， ∴OD＝OA＝ 쳌 ，CD＝2OB＝2a， ∴C（ 쳌 ，2a）， ∵反比例函数 y＝ （x＞0）的图象经过点 C， ∴k＝ 쳌 ×2a＝4． 故选 D． 7．（2019·江苏中考真题）当矩形面积一定时，下列图象中能表示它的长 y 和宽 x 之间函数关 系的是（ ） A． B． C． D． 【详解】 ∵根据题意 N 矩形面积（定值）， ∴y 是 x 的反比例函数， ൅ 䁠 ． 故选：B． 8．（2019·贵州中考真题）若点 A（﹣4，y1）、B（﹣2，y2）、C（2，y3）都在反比例函数 1y x   的图象上，则 y1、y2、y3 的大小关系是( ) A．y1＞y2＞y3 B．y3＞y2＞y1 C．y2＞y1＞y3 D．y1＞y3＞y2 【详解】 ∵点 A(﹣4，y1)、B(﹣2，y2)、C(2，y3)都在反比例函数 1y x   的图象上， ∴ N N ， N N ， N ， 又∵﹣ ＜ ＜ ， ∴y3＜y1＜y2， 故选 C. 9．（2018·吉林中考真题）如图，在平面直角坐标系中，等腰直角三角形 ABC 的顶点 A、B 分别在 x 轴、y 轴的正半轴上，∠ABC=90°，CA⊥x 轴，点 C 在函数 y= （x＞0）的图象上， 若 AB=2，则 k 的值为（ ） A．4 B．2 C．2 D． 【详解】作 BD⊥AC 于 D，如图， ∵△ABC 为等腰直角三角形， ∴AC= AB=2 ， ∴BD=AD=CD= ， ∵AC⊥x 轴， ∴C（ ，2 ）， 把 C（ ，2 ）代入 y= 得 k= ×2 =4， 故选 A． 10．（2018·黑龙江中考真题）在同一直角坐标系中，函数 y= 和 y=kx﹣3 的图象大致是（ ） A． B． C． D． 【详解】分两种情况讨论： ①当 k＞0 时，y=kx﹣3 与 y 轴的交点在负半轴，过一、三、四象限，反比例函数的图象在第 一、三象限； ②当 k＜0 时，y=kx﹣3 与 y 轴的交点在负半轴，过二、三、四象限，反比例函数的图象在第 二、四象限， 观察只有 B 选项符合， 故选 B． 11．（2015·湖北中考真题）在反比例函数 图象上有两点 A（ ， ）B（ ， ）， ＜0＜ ， ＜ ，则 m 的取值范围是（ ） A．m＞ B．m＜ C．m≥ D．m≤ 【详解】 对于反比例函数 y= ， 当 k＞0，在每个象限内，y 随 x 的增大而减小； 当 k＜0 时，在每个象限内，y 随 x 的增大而增大． 本题根据题意可得：k＞0，即 1－3m＞0，解得：m＜ ． 12．（2018·青海中考真题）若 䁠 ， 䁠 是函数 N 图象上的两点，当 时，下列结论正确的是 ൅ A． 䂄 䂄 B． 䂄 䂄 C． 䂄 䂄 D． 䂄 䂄 【详解】 把点 P1(x1，y1)，P2(x2，y2)代入 N 得 N ， N ， 则 N N ൅ ． ∵x1＞x2＞0， ∴ N ， N ， N ൅ 䂄 ， 即 0＜y1＜y2． 故选 A． 二、填空题（共 5 小题，每题 4 分，共计 20 分） 13．（2019·辽宁中考真题）如图，点 A 在双曲线 y＝ 6 x （x＞0）上，过点 A 作 AB⊥x 轴于 点 B，点 C 在线段 AB 上且 BC：CA＝1：2，双曲线 y＝ （x＞0）经过点 C，则 k＝_____． 【详解】 解：连接 OC， ∵点 A 在双曲线 y＝ 6 x （x＞0）上，过点 A 作 AB⊥x 轴于点 B， ∴S △ OAB＝ ×6＝3， ∵BC：CA＝1：2， . ＞ ＞ ：故答案为 根据题意得：当 y1>y2 时，x 的取值范围是 2＜x＜4， 【详解】 的取值范围是_____． 所示，当 1 2y y＞ 时，自变量 ）的图象如图 ＞ （ ＝ 与反比例函数 N ݔ 15．（2019·黑龙江中考真题）一次函数 故答案为：（﹣2，﹣4）． ∴另一个交点的坐标是（-2，-4）， ∵一个交点的坐标是（2，4）， ∴两函数的交点关于原点对称， ∵正比例函数和反比例函数均关于原点对称， 【详解】 坐标为（2，4），则它们另一个交点的坐标是_____． （k≠0）的图象一个交点 14．（2018·广西中考真题）已知直线 y=ax（a≠0）与反比例函数 y= 故答案为 2． ∴k＝2， （x＞0）在第一象限， ∵双曲线 y＝ ∴|k|＝2， |k|＝1， OBC＝ △ ∴S （x＞0）经过点 C， ∵双曲线 y＝ ＝1， OBC＝3× △ S∴ ． N ∴直线 BD 的解析式为 ， ＝ 得 ＝ ，解得 ＝ ݔ 得 ＝ ݔ 得 ）代入得 ， 把 D（5，3），B（ 设直线 BD 的解析式为 y=mx+n， ）， ， ∴B（ ）， ，3），C（5， ∴A（ ∵D（5，3）， 【详解】 的函数表达式是______. ，则直线 䁠 的坐标为 上，若顶点 ） ， （常数 N 都在曲线 䁠 的顶点 17．（2019·浙江中考真题）如图，矩形 ∴k＝6. ∴k>0， ∵图象在第一象限， |k|＝S 矩形 OABC＝6， 【详解】 __________． N ，则 N 矩形   的图像上， 在反比例函数 ( 0)ky xx 的顶点 甘肃中考真题）如图，矩形·2019）．16 ， N ， N （2）∵ ． N ∴ ， N N 解得： ， ݔ N ݔ N ∴ ， N ݔ 两点的一次函数表达式为： 、 设图象经过 ． N N ∴ ， ， ∵反比例函数图象过点 ． ， ， ， ∴ 的中点， 为 ， N ， N ， ， （1）∵ 【详解】 ，代入反比例函数解析式即可得到结论． ， 쳌 坐标为 ，则点 ， 쳌 坐标为 点 ．设 N ， N ，得到 N ，由 N ，得到 N ， N （2）由 （1）由已知求出 A、E 的坐标，即可得出 m 的值和一次函数函数的解析式； ，求反比例函数的表达式. N （2）若 两点的一次函数的表达式； 、 的值及图象经过 ，求 ൅ 䁠 坐标为 （1）若点 . 交于点 ，与 的图象经过点 N 中点，反比例函数 的 是 的长分别为 3、8， 、 的两边 18．（2018·山东中考真题）如图，矩形 三、解答题（共 4 小题，每题 8 分，共计 32 分） ． N 故答案为 ∴ N ． ∵ N ， ∴ N ， ∴ N ． 设 点坐标为 쳌 ， ，则点 坐标为 쳌 ， ． ∵ ， 两点在 N 图象上， ∴ 쳌 N 쳌 ， 解得： 쳌 N ， ∴ ， ， ∴ N ， ∴ N ． 19．（2019·江苏中考真题）如图，在▱ 中， N ， 45AOC   ，点 在 轴上， 点 是 的中点，反比例函数 N 的图象经过点 、 （1）求 的值；（2）求点 的坐标． 【名师点拨】 （1）根据已知条件求出 点坐标即可； （2）四边形 是平行四边形 ，则有 轴，可知 的横纵标为 ， 点的横 坐标为 ，结合解析式即可求解； 【详解】 （1） N ， 45AOC   ， 䁠 ， N ， N ； （2）四边形 是平行四边形 ， 轴， 的横纵标为 ， 点 是 的中点， 点的横坐标为 ， 䁠 ； 20．（2018·四川中考真题）如图，已知一次函数 y=kx+b 的图象与反比例函数 y= 的图象交于 A，B 两点，点 A 的横坐标是 2，点 B 的纵坐标是－2． （1）求一次函数的解析式； （2）求 △ AOB 的面积． 【名师点拨】 （1）由点 A、B 的横纵坐标结合反比例函数解析式即可得出点 A、B 的坐标，再由点 A、B 的坐标利用待定系数法即可得出直线 AB 的解析式； （2）先找出点 C 的坐标，利用三角形的面积公式结合 A、B 点的纵坐标即可得出结论． 【详解】 （1）反比例函数 y= ，x=2，则 y=4， ， =（1）由表格中数据可得：y 【详解】 (3)利用 w=1200 进而得出答案． (2)直接利用 y=300 代入求出答案； (1)直接利用反比例函数解析式求法得出答案； 【名师点拨】 （3）在（2）的基础上，超市销售该种水果能否到达每周获利 1200 元？说明理由． 每千克售价最多定为多少元？ （2）由于销售淡季即将来临，超市要完成每周销售量不低于 300 千克的任务，则该种水果 （1）写出每周销售量 y（千克）与每千克售价 x（元）的函数关系式； 每周销售量 y（千克） 240 200 150 每千克售价 x（元） 25 30 40 与每千克售价 x（元）的关系如表所示 通过一段时间的销售情况发现，该种水果每周的销售总额相同，且每周的销售量 y（千克） 21．（2019·青岛市中考模拟）某果品超市经销一种水果，已知该水果的进价为每千克 15 元， ×2×[2-（-4）]=6． OC•（xA-xB）= AOB= △ ∴S ∴点 C 的坐标为（0，2）， （2））令 y=x+2 中 x=0，则 y=2， ∴一次函数的解析式为 y=x+2． ． N N ݔ N 解得： ݔ N ∴ ∵一次函数过 A、B 两点， ∴点 B 的坐标为（-4，-2）． ，解得：x=-4， 中 y=-2，则-2= 反比例函数 y= 点 A 的坐标为（2，4）；∴ 把（30，200）代入得： y= ； （2）当 y=300 时，300= ， 解得：x=20，即该种水果每千克售价最多定为 20 元； （3）由题意可得：w=y（x-15）= （x-15）=1200， 解得：x= 经检验：x= 是原方程的根， 答：超市销售该种水果能到达每周获利 1200 元．