2019九年级数学下册 专题突破讲练 建立适当的坐标系解决实际问题试题 （新版）青岛版

2019九年级数学下册 专题突破讲练 建立适当的坐标系解决实际问题试题 （新版）青岛版

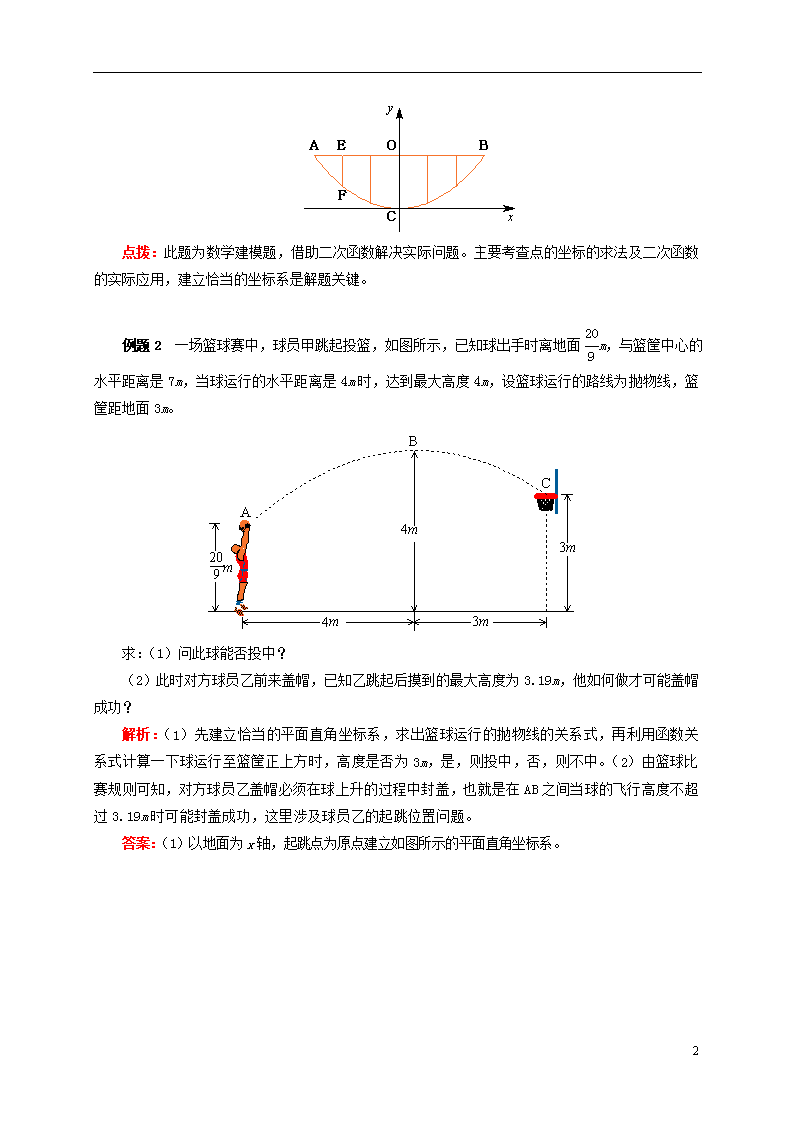
建立适当的坐标系解决实际问题 一、建立坐标系解决实际问题的一般步骤 ‎1. 恰当地建立直角坐标系；‎ ‎2. 将已知条件转化为点的坐标；‎ ‎3. 合理地设出所求函数关系式；‎ ‎4. 代入已知条件或点的坐标，求出关系式；‎ ‎5. 利用关系式求解问题。‎ 方法归纳：（1）恰当地建立直角坐标系是准确、简捷地求解问题的关键；‎ ‎（2）将已知条件转化为点的坐标时，应注意距离与坐标的关系；‎ ‎（3）设函数关系式应根据题设合理选择三种函数式中的一种；‎ ‎（4）求解问题应能将点的坐标正确地转化为距离或高度。‎ 总结：‎ ‎1. 能分析实际问题中数量关系，建立二次函数模型。‎ ‎2. 能够建立坐标系，确定二次函数关系式，并解决实际问题。‎ 例题1 如图，某校的围墙由一段相同的凹曲拱组成，其拱状图形为抛物线的一部分，栅栏的跨径AB之间按相同间隔‎0.2米用5根立柱加固，拱高OC为‎0.36米，则立柱EF的长为（ ）‎ A. ‎0.4‎米‎ B. ‎0.16米 C. ‎0.2米 D. ‎‎0.24米 解析：由于按相同的间距‎0.2m用5根立柱加固，则AB＝0.2×6＝1.2，以C为坐标系的原点，OC所在直线为y轴建立坐标系，由此得到抛物线过B（0.6，0.36）、C（0，0）、A（－0.6，0.36），据此求出其解析式。把x＝－0.4代入后求出y，令EF=0.36－y即可。‎ 答案：如图，以C为坐标系的原点，OC所在直线为y轴建立坐标系，设抛物线解析式为y＝ax2，由题意知，图象过B（0.6，0.36），代入得：0.36＝‎0.36a，∴a＝1，即y＝x2。∵F点横坐标为－0.4，∴当x＝－0.4时，y＝0.16，∴EF＝0.36－0.16＝‎0.2米。故选C。‎ 13‎ 点拨：此题为数学建模题，借助二次函数解决实际问题。主要考查点的坐标的求法及二次函数的实际应用，建立恰当的坐标系是解题关键。‎ 例题2 一场篮球赛中，球员甲跳起投篮，如图所示，已知球出手时离地面m，与篮筐中心的水平距离是‎7m，当球运行的水平距离是‎4m时，达到最大高度‎4m，设篮球运行的路线为抛物线，篮筐距地面‎3m。‎ 求：（1）问此球能否投中？‎ ‎（2）此时对方球员乙前来盖帽，已知乙跳起后摸到的最大高度为‎3.19m，他如何做才可能盖帽成功？‎ 解析：（1）先建立恰当的平面直角坐标系，求出篮球运行的抛物线的关系式，再利用函数关系式计算一下球运行至篮筐正上方时，高度是否为‎3m，是，则投中，否，则不中。（2）由篮球比赛规则可知，对方球员乙盖帽必须在球上升的过程中封盖，也就是在AB之间当球的飞行高度不超过‎3.19m时可能封盖成功，这里涉及球员乙的起跳位置问题。‎ 答案：（1）以地面为x轴，起跳点为原点建立如图所示的平面直角坐标系。‎ 13‎ 由题意知，抛物线顶点坐标为（4，4），经过（0，）。‎ 设抛物线的关系式为y＝a（x－4）2＋4，‎ 把x＝0，y＝代入，得＝a（0－4）2＋4，‎ ‎∴a＝－。‎ ‎∴y＝－（x－4）2＋4，即y＝－x2＋x＋。‎ 当x＝7时，y＝－（7－4）2＋4＝3，‎ 而篮筐中心距地面刚好是‎3m，∴此球能够投中。‎ ‎（2）当y＝3.19时，－（x－4）2＋4＝3.19，解得x1＝1.3，x2＝6.7。‎ 由于篮球比赛规则规定盖帽必须在球上升过程中，‎ 当x＝1.3时上升，当x＝6.7时下降。‎ 所以，球员乙必须在球员甲前‎1.3m之内跳起封盖才可能成功。‎ 点拨：本例通过建立平面直角坐标系求出二次函数的关系式，再利用二次函数的有关性质来解决实际问题，将实际问题转化为数学模型是关键，而利用数学知识去解决实际问题时还要注意符合实际意义。‎ 有些实际问题中并没有明确给出它符合哪一种函数，这时应根据题目提供的数据画出图象，根据图象判断函数的种类。若所给数据符合二次函数特征，可选取三组数据（即三点）求出二次函数的关系，但必须将其他点代入验证，这一步不可少，只有验证无误后方可认定是二次函数，以防错误判断。‎ 例 行驶中的汽车，在刹车后由于惯性的作用，还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”。为了测定某型号汽车的刹车性能（车速不能超过‎140km/h 13‎ ‎），对这种汽车进行测试，测得数据如下：‎ 刹车时 车速（km/h）‎ ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ 刹车距离 ‎（m）‎ ‎0‎ ‎0.3‎ ‎1.0‎ ‎2.1‎ ‎3.6‎ ‎5.5‎ ‎7.8‎ ‎（1）以车速为x轴，以刹车距离为y轴，在坐标系中描出这些数据所表示的点，并用平滑的曲线联结这些点，得到函数的大致图象；‎ ‎（2）观察图象，估计函数的类型；‎ ‎（3）如果该函数解析式为y＝0.002x2＋0.01x，若该型号汽车在国道上发生了一次交通事故，现场测得刹车距离为‎46.5m，请推测刹车时的速度，在事故发生时，汽车是超速行驶还是正常行驶？‎ 解：（1）描点，画图如下：‎ ‎（2）依据图象，设抛物线的关系式为y＝ax2＋bx＋c，将表中前三对数据代入，得 ，解得。‎ 所以函数关系式为y＝0.002x2＋0.01x（0≤x≤140）。‎ 经检验，表中其他各组数据也符合此关系式。‎ ‎（3）当y＝46.5时，0.002x2＋0.01x＝46.5，‎ 解此方程，得x1＝150，x2＝－155（舍去）。‎ 所以推测刹车的速度是‎150km/h，因为150＞140，所以事故发生时，汽车超速行驶。‎ 解析：解答这类问题时应将表中每一组数据作为点的坐标，在坐标系内描出这些点，画出图象，注意隐含条件。再根据所画的图象，判断出y是x的什么函数，然后用待定系数法求函数关系式。‎ 一、选择题 13‎ ‎1. 教练对小明推铅球的录像进行技术分析，发现铅球行进高度y（m）与水平距离x（m）之间的关系为y＝－（x－4）2＋3，由此可知铅球推出的距离是（ ）‎ A. ‎3m B. ‎6m C. ‎10m D. ‎‎12m ‎2. 某公园草坪的防护栏是由150段形状相同的抛物线组成的。为了牢固起见，每段护栏需要间距‎0.4m加设一根不锈钢的支柱，防护栏的最高点距底部‎0.5m（如图），则这条防护栏需要不锈钢支柱的总长度至少为（ ）‎ A. ‎240m B. ‎200m C. ‎160m D. ‎‎150m ‎3. 如图是一副眼镜镜片下半部分轮廓对应的两条抛物线，关于y轴对称。AB∥x轴，AB＝‎4cm，最低点C在x轴上，高CH＝‎1cm，BD＝‎2cm。则右轮廓线DFE所在抛物线的函数解析式为（ ）‎ A. y＝（x＋3）2 B. y＝－（x＋3）2‎ C. y＝（x－3）2 D. y＝－（x－3）2‎ ‎*4. 如图是某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是‎1m，拱桥的跨度为‎10m，桥洞与水面的最大距离是‎5m，桥洞两侧壁上各有一盏距离水面‎4m的景观灯。若把拱桥的截面图放在平面直角坐标系中，则两盏景观灯之间的水平距离是（ ）‎ 13‎ A. ‎3m B. ‎4m C. ‎5m D. ‎‎6m ‎**5. 为了备战世界杯，中国足球队在某次训练中，一队员在距离球门‎12m处的挑射正好射中了‎2.4m高的球门横梁，若足球运行的路线是抛物线y＝ax2＋bx＋c（如图所示）则下列结论：①a＜－，②－＜a＜0，③a－b＋c＞0，④0＜b＜－‎24a，其中正确的结论是（ ）‎ A. ①③ B. ①④ C. ②③ D. ②④‎ ‎**6. 一块边缘呈抛物线形的铁片如图放置，测得AB＝‎20cm，抛物线的顶点到AB边的距离为‎25cm。现要沿AB边向上依次截取宽度均为‎4cm的矩形铁皮，如图所示。已知截得的铁皮中有一块是正方形，则这块正方形铁皮是（ ）‎ A. 第七块 B. 第六块 C. 第五块 D. 第四块 二、填空题 ‎7. ‎2013年5月26日，中国羽毛球队蝉联苏迪曼杯团体赛冠军，成就了首个五连冠霸业。比赛中羽毛球的某次运动路线可以看作是一条抛物线（如图）。若不考虑外力因素，羽毛球行进高度y（米）与水平距离x（米）之间满足关系y＝－x2＋x＋，则羽毛球飞出的水平距离为__________米。‎ 13‎ ‎8. 兰州市“安居工程”新建成的一批楼房都是8层高，房子的价格y（元/平方米）随楼层数x（楼）的变化而变化（x＝1，2，3，4，5，6，7，8）；已知点（x，y）都在一个二次函数的图象上（如图所示），则6楼房子的价格为__________元/平方米。‎ ‎*9. 如图是我省某地一座抛物线形拱桥，桥拱在竖直平面内，与水平桥面相交于A、B两点，桥拱最高点C到AB的距离为‎9m，AB＝‎36m，D、E为桥拱底部的两点，且DE∥AB，点E到直线AB的距离为‎7m，则DE的长为__________m。‎ ‎**10. 甲、乙两人进行羽毛球比赛，甲发出一颗十分关键的球，出手点为P，羽毛球飞行的水平距离s（米）与其距地面高度h（米）之间的关系式为h＝－s2＋s＋。如图，已知球网AB距原点‎5米，乙（用线段CD表示）扣球的最大高度为米，设乙的起跳点C的横坐标为m，若乙原地起跳，因球的高度高于乙扣球的最大高度而导致接球失败，则m的取值范围是__________。‎ 三、解答题 ‎*11. ‎ 13‎ 如图，有一块铁皮，拱形边缘呈抛物线状，MN＝4分米，抛物线顶点处到边MN的距离是4分米，要在铁皮上截下一矩形ABCD，使矩形顶点B、C落在边MN上，A、D落在抛物线上，问这样截下的矩形铁皮的周长能否等于8分米？‎ ‎*12. 如图，人工喷泉有一个竖直的喷水枪AB，喷水口A距地面‎2米，喷水水流的轨迹是抛物线，如果要求水流的最高点P到喷水枪AB所在直线的距离为‎1米，且水流着地点C距离水枪底部B的距离为米，那么水流的最高点距离地面是多少米？‎ ‎*13. 实践应用：下承式混凝土连续拱圈梁组合桥，其桥面上有三对抛物线形拱圈。图（1）是其中一个拱圈的实物照片，据有关资料记载，此拱圈高AB为‎10.0m（含拱圈厚度和拉杆长度），横向分跨CD为‎40.0m。‎ ‎（1）试在示意图（图（2））中建立适当的直角坐标系，求出拱圈外沿抛物线的解析式；‎ ‎（2）在桥面M（BC的中点）处装有一盏路灯（P点），为了保障安全，规定路灯距拱圈的距离PN不得少于‎1.1m，试求路灯支柱PM的最低高度。（结果精确到‎0.1m）‎ ‎**14. 如图，有一条双向公路隧道，其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成，隧道最大高度为4.‎9米，AB＝‎10米，BC＝‎2.4米，若有一辆高为‎4米、宽为‎2米的集装箱的汽车要通过隧道，为了使箱顶不碰到隧道顶部，又不违反交通规则（汽车应靠道路右侧行驶，不能超过道路中线），汽车的右侧必须离开隧道右壁几米？‎ ‎**15. 如图所示，足球场守门员在O处开出一高球，球从离地面‎1米的A处飞出（A在y轴上），运动员乙在距O点‎6米的B处发现球在自己正上方达到最高点M，距地面约‎4米高，球落地后又一次弹起，据实验，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半。‎ 13‎ ‎（1）求足球开始飞出到第一次落地时，该抛物线的表达式；‎ ‎（2）足球第一次落地点C距守门员多少米？（取4＝7）‎ ‎（3）运动员乙要抢到第二个落点D，他应再向前跑多少米？（取2＝5）‎ 13‎ 一、选择题 ‎1. C 解析：令函数式y＝－（x－4）2＋3中，y＝0，0＝－（x－4）2＋3，解得x1＝10，x2＝－2（舍去），即铅球推出的距离是‎10m。‎ ‎2. A 解析：建立平面直角坐标系，可设抛物线解析式为y＝ax2＋0.5，∵（1，0）在抛物线上，∴a＋0.5＝0，解得a＝－0.5，∴y＝－0.5x2＋0.5，当x＝0.2时y＝0.48，当x＝0.6时y＝0.32，∴一段防护栏需要不锈钢支柱的总长＝2×（0.48＋0.32）＝‎1.6米，∴所需不锈钢管的总长度为：1.6×150＝‎240米。故选A。‎ ‎3. C 解析：∵高CH＝‎1cm，BD＝‎2cm，而B、D关于y轴对称，∴D点坐标为（1，1），∵AB∥x轴，AB＝‎4cm，最低点C在x轴上，∴AB关于直线CH对称，∴左边抛物线的顶点C的坐标为（－3，0），∴右边抛物线的顶点F的坐标为（3，0），设右边抛物线的解析式为y＝a（x－3）2，把D（1，1）代入得1＝a×（1－3）2，解得a＝，故右边抛物线的解析式为y＝（x－3）2。故选C。‎ ‎*4. C 解析：抛物线的顶点坐标为（5，5），且经过点（0，1），设抛物线解析式为y＝a（x－5）2＋5，把点（0，1）代入得：1＝a（0－5）2＋5，即a＝－，∴抛物线解析式为y＝－（x－5）2＋5。令y＝4，得x1＝，x2＝，∴盏景观灯之间的水平距离是－＝‎5m。‎ ‎**5. B 解析：由抛物线的开口向下知a＜0，对称轴为x＝－＞0，∴a、b异号，即b＞0。与y轴的交点坐标为（0，2.4），∴c＝2.4，把点（12，0）代入解析式，得：‎144a＋12b＋2.4＝0。∴‎144a＝－2.4－12b，12b＝－2.4－‎144a，由以上两式分别可得‎144a＜－2.4，12b＜－‎144a，∴a＜－，b＜－‎12a，∴2b＜－‎24a，则b＜－‎24a，∴①④正确，②错误。∵此题是实际问题，∴x不能取－1，∴③a－b＋c＞0错误。故选B。‎ ‎**6. B 解：如图，建立平面直角坐标系。∵AB＝‎20cm，抛物线的顶点到AB边的距离为‎25cm，∴此抛物线的顶点坐标为（10，25），图象与x轴的交点坐标为：（0，0），（20，0），∴抛物线的解析式为：y＝a（x－10）2＋25，解得：0＝‎100a＋25，a＝－，∴y＝－（x－10）2＋25，现要沿AB边向上依次截取宽度均为‎4cm的矩形铁皮，∴截得的铁皮中有一块是正方形时，正方形边长一定是‎4cm。∴当四边形DEFM是正方形时，DE＝EF＝MF＝DM＝‎4cm，∴M点的横坐标为AN－MK＝10－2＝8，即x＝8，代入y＝－（x－10）2＋25，解得：y＝24，∴KN＝24，24÷4＝6，∴这块正方形铁皮是第六块，故选B。‎ 13‎ 二、填空题 ‎7. 5 解析：当y＝0时，0＝－x2＋x＋，解得：x1＝－1（舍），x2＝5，故羽毛球飞出的水平距离为‎5m。‎ ‎8. 2080 解析：由图可知此二次函数图象的顶点是（4，2200），设其表达式为y＝a（x－4）2＋2200，又因为它过点（2，2080），所以2080＝a（2－4）2＋2200，解得a＝－30，即y＝－30（x－4）2＋2200，当x＝6时，y＝－30（6－4）2＋2200＝2080（元/平方米）。或利用抛物线的对称性，观察图象可知当x＝6时与x＝2时的函数值y相等，即6楼的价格也是2080元/平方米。‎ ‎*9. 48 解析：以C为原点建立平面直角坐标系，依题意，得B（18，－9），设抛物线为：y＝ax2，将B点坐标代入，得a＝－，所以抛物线为y＝－x2，E点到x轴距离为9＋7＝16（米），所以E点纵坐标为y＝－16，代入得－16＝－x2，解得x＝±24，所以DE的长为‎48m。‎ ‎**10. 5＜m＜4＋ 解析：先求乙恰好扣中的情况，当h＝时，－m2＋m＋＝，解方程得：m1＝4＋，m2＝4－，但扣球点必须在球网右边，即m＞5，∴m2＝4－（舍去），由于乙原地起跳，因球的高度高于乙扣球的最大高度而导致接球失败，∴5＜m＜（4＋）。‎ 三、解答题 ‎*11. 解：以MN为x轴，MN的垂直平分线为y轴建立平面直角坐标系，则M（－2，0）、N（2，0），该抛物线顶点坐标为（0，4），所以其解析式可设为y＝ax2＋4，将M的坐标代入得0＝‎4a＋4，所以a＝－1，即y＝－x2＋4。设点A的坐标为（m，n），则n＝－m2＋4，若矩形铁皮的周长为8分米，则2（－m2＋4）＋‎4m＝8，解得m1＝0，m2‎ 13‎ ‎＝2，均不符合题意，舍去。所以不能截下周长为8分米的矩形。‎ ‎*12. 解：要想求出水流最高点距地面高度，可以先以B为原点，地面为x轴建立直角坐标系，由题目可知水流抛物线过点A（0，2）、C（，0），因为点P的横坐标是1，由抛物线的对称性知它与x轴的另一交点为（－，0），根据这三个点求出抛物线解析式为y＝－x2＋x＋2。当x＝1时y＝3.6，即最高点P的坐标为（1，3.6），所以水流的最高点距离地面是‎3.6米。‎ ‎*13. 解：（1）如图，以A为坐标原点，BA所在直线为y轴建立直角坐标系xAy，因拱圈外沿所在的抛物线过原点，且以y轴为对称轴，故可设抛物线解析式为：y＝ax2，由题意知抛物线过点D（20，－10），代入得：a＝－，故拱圈外沿抛物线的解析式为y＝－x2。（2）设N（－10，k），则k＝－×（－10）2＝－2.5，∴MN＝10－︱k︱＝7.5（m），∴PM＝MN＋PN≥7.5＋1.1＝8.6（m）。即路灯支柱PM的最低高度为‎8.6米。‎ ‎**14. 解：如下图，以CD为x轴，CD的垂直平分线为y轴建立平面直角坐标系，OM＝4.9－2.4＝‎2.5米，则C（5，0）、D（－5，0）、M（0，2.5），设该抛物线的解析式为y＝ax2＋2.5，则‎25a＋2.5＝0，解得a＝－0.1，所以y＝－0.1x2＋2.5，当y＝4－2.4＝1.6时，－0.1x2＋2.5＝1.6，解得x＝±3，则BH＝5－3＝‎2米。所以汽车右侧必须离开隧道右壁‎2米以上且不能超过‎3米。‎ ‎**15. 解：（1）设第一次落地前抛物线为y＝a（x－6）2＋4。∵其过点A（0，1），∴a（0－6）2＋4＝1，∴a＝－。∴抛物线表达式为y1＝－（x－6）2＋4＝－x2＋x＋1。（2）当y1＝0时，有－（x－6）2＋4＝0，解得x＝4＋6≈13（米）（取正根）。即第一次落地点C到守门员的距离为‎13米。（3）由（2）得C点（13，0），设抛物线CND的表达式为y2＝－（x－k）2＋2，当x＝13，y2＝0时，有－（13－k）2＋2＝0，解得k＝13＋2≈18（米）（取正根），∴有y2＝－（x－18）2＋2。对此当y2＝0时，－（x－18）2＋2＝0，解得x＝18＋2 13‎ ‎≈23（米）（取正根），∴BD＝OD－OB＝23－6＝17（米）。所以运动员乙应再向前跑‎17米。‎ 13‎