2020年秋九年级数学上册 第3章圆

2020年秋九年级数学上册 第3章圆

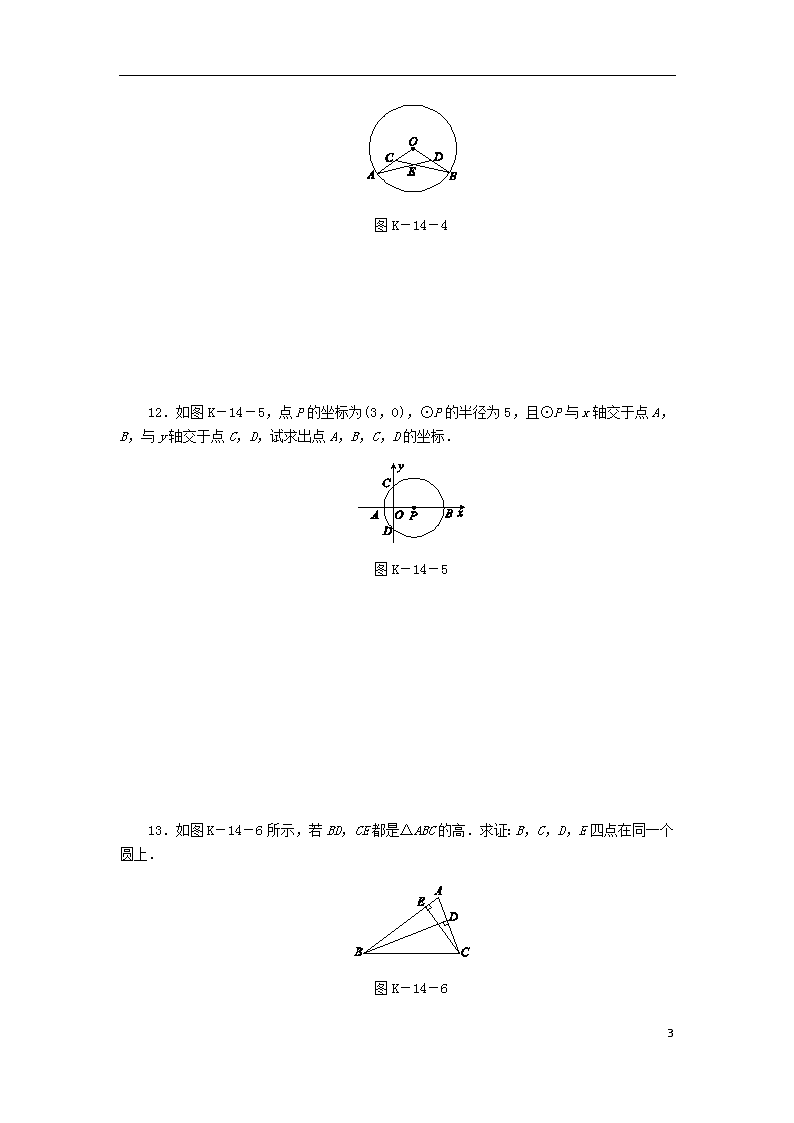
‎3．1　圆 ‎3.1　第1课时　圆的有关概念　　　　　　　　　　　　　　　　‎ 一、选择题 ‎1．下列结论正确的是(　　)‎ A．半径是弦 ‎ B．弧是半圆 C．大于半圆的弧是优弧 ‎ D．弦所对的弧一定是劣弧 ‎2．已知⊙O的半径为‎5 cm，P是⊙O外一点，则OP的长可能是(　　)‎ A．‎3 cm B．‎4 cm ‎ C．‎5 cm D．‎‎6 cm ‎3．2017·张家界如图K－14－1，在⊙O中，AB是直径，AC是弦，连结OC，若∠ACO＝30°，则∠BOC的度数是(　　)‎ 图K－14－1‎ A．30° B．45° C．55° D．60°‎ ‎4．如图K－14－2所示，在Rt△ABC中，∠C＝90°，AB＝10，若以点C为圆心，CB长为半径的圆恰好经过AB的中点D，则AC的长等于(　　)‎ ‎　　‎ 图K－14－2‎ A．5 B．‎5 C．5 D．6‎ 9‎ ‎5．AB是⊙O的弦，OQ⊥AB于点Q，再以OQ为半径作同心圆，称作小⊙O，P是AB上异于点A，B，Q的任意一点，则点P的位置是(　　)‎ A．在大⊙O上 ‎ B．在大⊙O外部 C．在小⊙O内部 ‎ D．在小⊙O外而在大⊙O内 ‎6．如图K－14－3，点B，E，G，M在半圆O上，四边形ABCO，ODEF，OHMN都是矩形，设AC＝a，DF＝b，NH＝c，则下列各式中正确的是(　　)‎ 图K－14－3‎ A．a>b>c B．a＝b＝c C．c>a>b D．b>c>a 二、填空题 ‎7．菱形四边的中点到____________的距离相等，因此菱形各边的中点在以____________为圆心，以____________为半径的圆上．‎ ‎8．已知⊙A的半径为6.5，圆心A的坐标为(－6，0)，点B的坐标是(0，3)，则点B与⊙A的位置关系是______________．‎ ‎9．在同一平面上，点P到⊙O上一点的距离最长为‎6 cm，最短为‎2 cm，则⊙O的半径为________ cm.‎ ‎10．在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙A的半径为2，若点B在⊙A内，则a的取值范围是________. 三、解答题 ‎11．如图K－14－4，OA，OB为⊙O的半径，C，D分别为OA，OB的中点．求证：∠A＝∠B.‎ 9‎ 图K－14－4‎ ‎12．如图K－14－5，点P的坐标为(3，0)，⊙P的半径为5，且⊙P与x轴交于点A，B，与y轴交于点C，D，试求出点A，B，C，D的坐标．‎ 图K－14－5‎ ‎13．如图K－14－6所示，若BD，CE都是△ABC的高．求证：B，C，D，E四点在同一个圆上．‎ 图K－14－6‎ 9‎ ‎14．如图K－14－7，在△ABC中，∠C＝90°，BC＝‎3 cm，AC＝‎4 cm.‎ ‎(1)以点B为圆心，BC长为半径画⊙B，点A，C及AB的中点E与⊙B有怎样的位置关系？‎ ‎(2)以点A为圆心，R为半径画⊙A，若B，C，E三点中至少有一点在圆内，至少有一点在圆外，则⊙A的半径R应满足什么条件？ ‎　图K－14－7‎ ‎15．如图K－14－8，线段AB＝‎8 cm，点D从A点出发沿AB向B点匀速运动，速度为‎1 cm/s，同时点C从B点出发沿BA向A点以相同速度运动，以点C为圆心，‎2 cm长为半径作⊙C，点D到达B点时⊙C也停止运动，设运动时间为t s，求点D在⊙C内部时t的取值范围．‎ 图K－14－8‎ 9‎ ‎16．如图K－14－9所示，铁路MN和公路PQ在点O处交汇，∠QON＝30°，公路PQ上A处距离O点‎240米，如果火车行驶时，周围‎200米以内会受到噪音的影响，那么火车在铁路MN上沿MN方向以72千米/时的速度行驶时，A处受到噪音影响的时间为多少？‎ 图K－14－9‎ 9‎ ‎1．[答案] C 9‎ ‎2．[解析] D　∵P是⊙O外一点，∴OP>‎5 cm，∴OP可能是‎6 cm.‎ ‎3．[答案] D ‎4．[解析] A　连结CD.在Rt△ABC中，∠ACB＝90°，AD＝BD，∴CD＝AB＝BC.‎ 根据勾股定理，得AC＝＝＝5 .故选A.‎ ‎5．[答案] D ‎6．[答案] B ‎7．[答案] 对角线的交点　对角线的交点　边长的一半 ‎8．[答案] 点B在⊙A外 ‎[解析] 在平面直角坐标系内，由勾股定理得BA＝＝＝3 >6.5，所以点B在⊙A外．‎ ‎9．[答案] 2或4‎ ‎10．[答案] 1＜a＜5‎ ‎[解析] ∵⊙A的半径为2，点B在⊙A内，‎ ‎∴AB＜2.∵点A所表示的实数为3，‎ ‎∴1＜a＜5.‎ ‎11．证明：∵OA＝OB，C，D分别为OA，OB的中点，∴OD＝OC.又∵∠O＝∠O，∴△AOD≌△BOC，∴∠A＝∠B.‎ ‎12．解：∵点P的坐标为(3，0)，∴OP＝3.‎ 又⊙P的半径为5，‎ ‎∴CO＝OD＝4，‎ ‎∴点C的坐标为(0，4)，点D的坐标为(0，－4)．‎ ‎∵⊙P的半径为5，∴AO＝2，PB＝5，‎ ‎∴点A的坐标为(－2，0)，OB＝8，‎ ‎∴点B的坐标为(8，0)．‎ ‎13．证明：如图所示，取BC的中点F，连结DF，EF.‎ 9‎ ‎∵BD，CE是△ABC的高，‎ ‎∴△BCD和△BCE都是直角三角形，‎ ‎∴DF，EF分别为Rt△BCD和Rt△BCE斜边上的中线，‎ ‎∴DF＝EF＝BF＝CF，‎ ‎∴B，C，D，E四点在以点F为圆心，BC长为半径的圆上．‎ ‎14．解：(1)∵∠C＝90°，∴AB2＝AC2＋BC2，‎ ‎∴AB＝5 cm.‎ ‎∵⊙B的半径BC＝3 cm，∴AB＞BC，‎ ‎∴点A在⊙B外．‎ 又∵BC＝3 cm，∴点C在⊙B上．‎ ‎∵AB＝5 cm，E是AB的中点，‎ ‎∴BE＝AB＝ cm＜3 cm，∴点E在⊙B内．‎ ‎(2) cm＜R＜‎5 cm.‎ ‎15．解：∵点C，D的运动速度相同，相向运动，‎ ‎⊙C的半径为2 cm，‎ ‎∴当点D第一次在⊙C上时，点D运动了＝3(s)，即t1＝3；‎ 当点D第二次在⊙C上时，点D运动了＝5(s)，即t2＝5.‎ ‎∴当点D在⊙C内部时，t的取值范围是3＜t＜5.‎ ‎16．解：如图，过点A作AC⊥ON于点C，设火车到B点时开始对A处有噪音影响，直到火车到D点后噪音才消失，连结AB，AD，则AB＝AD＝‎200米．‎ 9‎ ‎∵∠QON＝30°，OA＝240米，∴AC＝120米．‎ 当火车到B点时对A处产生噪音影响，此时AB＝200米，∵AB＝200米，AC＝120米，‎ ‎∴由勾股定理得BC＝160米，同理可得CD＝160米，即BD＝320米．‎ ‎∵72千米/时＝20米/秒，‎ ‎∴A处受到噪音影响的时间应是320÷20＝16(秒)．‎ 9‎