九年级上册数学同步练习24-1-2 垂直于弦的直径 人教版

九年级上册数学同步练习24-1-2 垂直于弦的直径 人教版

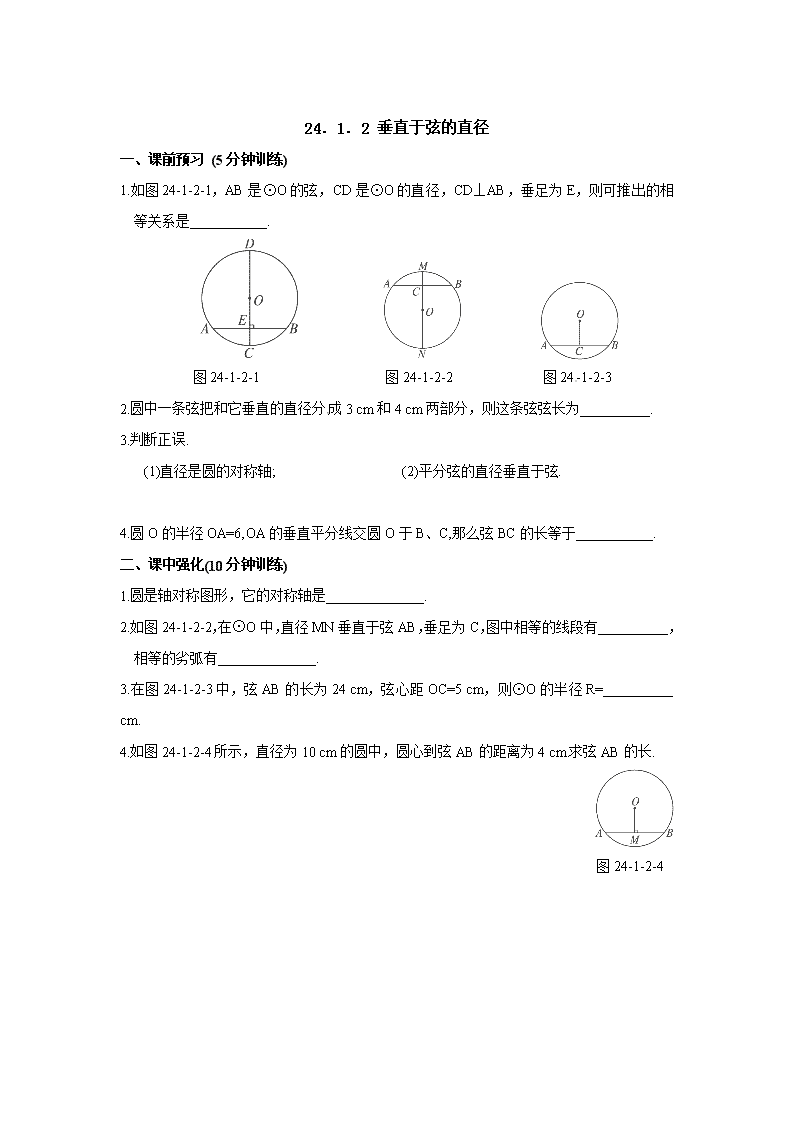
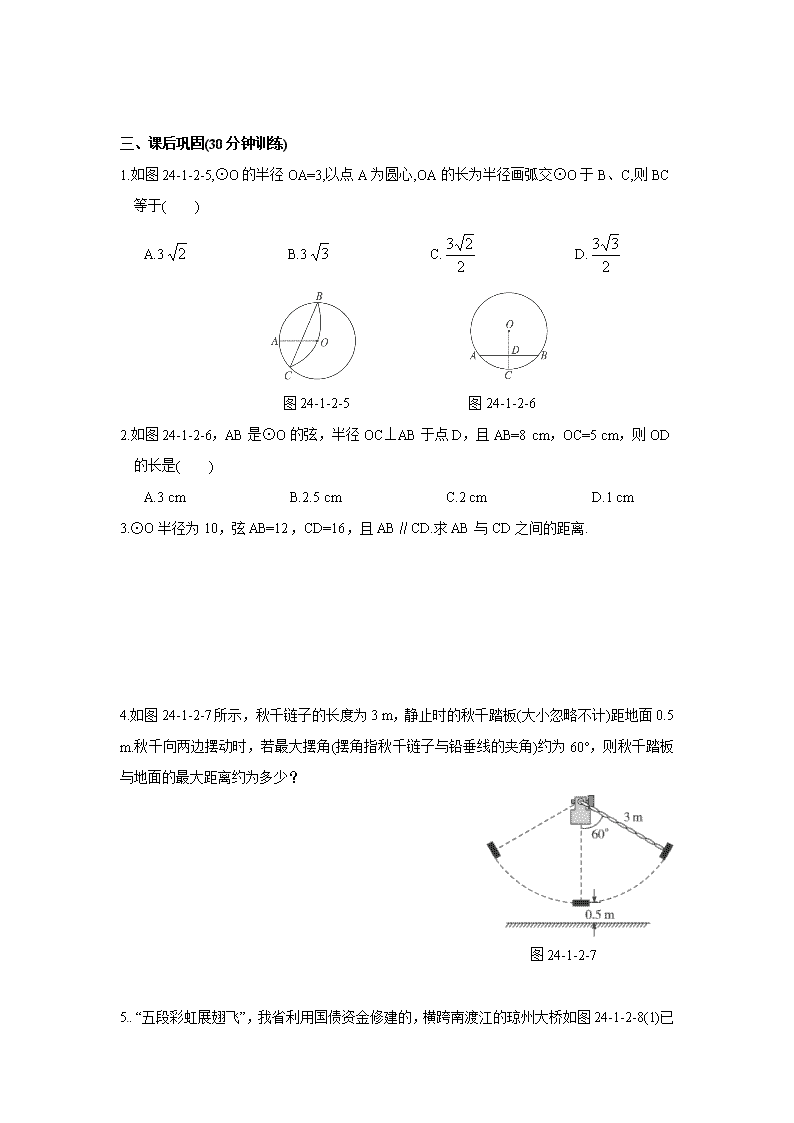
‎24．1．2 垂直于弦的直径 一、课前预习 (5分钟训练)‎ ‎1.如图24-1-2-1，AB是⊙O的弦，CD是⊙O的直径，CD⊥AB，垂足为E，则可推出的相等关系是___________.‎ ‎ ‎ 图24-1-2-1 图24-1-2-2 图24-1-2-3‎ ‎2.圆中一条弦把和它垂直的直径分成3 cm和4 cm两部分，则这条弦弦长为__________.‎ ‎3.判断正误.‎ ‎(1)直径是圆的对称轴; (2)平分弦的直径垂直于弦.‎ ‎4.圆O的半径OA=6,OA的垂直平分线交圆O于B、C,那么弦BC的长等于___________.‎ 二、课中强化(10分钟训练)‎ ‎1.圆是轴对称图形，它的对称轴是______________.‎ ‎2.如图24-1-2-2，在⊙O中，直径MN垂直于弦AB，垂足为C，图中相等的线段有__________，相等的劣弧有______________.‎ ‎3.在图24-1-2-3中，弦AB的长为24 cm，弦心距OC=5 cm，则⊙O的半径R=__________ cm.‎ ‎4.如图24-1-2-4所示，直径为10 cm的圆中，圆心到弦AB的距离为4 cm.求弦AB的长.‎ ‎ 图24-1-2-4‎ 三、课后巩固(30分钟训练)‎ ‎1.如图24-1-2-5,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC等于( )‎ A.3 B.3 C. D.‎ ‎ ‎ 图24-1-2-5 图24-1-2-6‎ ‎2.如图24-1-2-6，AB是⊙O的弦，半径OC⊥AB于点D，且AB=8 cm，OC=5 cm，则OD的长是( )‎ A.3 cm B.2.5 cm C.2 cm D.1 cm ‎3.⊙O半径为10，弦AB=12，CD=16，且AB∥CD.求AB与CD之间的距离.‎ ‎4.如图24-1-2-7所示，秋千链子的长度为3 m，静止时的秋千踏板(大小忽略不计)距地面0.5 m.秋千向两边摆动时，若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°，则秋千踏板与地面的最大距离约为多少？‎ ‎ 图24-1-2-7‎ ‎5. “五段彩虹展翅飞”，我省利用国债资金修建的，横跨南渡江的琼州大桥如图24-1-2-8(1)‎ 已于今年5月12日正式通车，该桥的两边均有五个红色的圆拱，如图24-1-2-8(1).最高的圆拱的跨度为110米，拱高为22米，如图(2),那么这个圆拱所在圆的直径为___________米.‎ ‎ 图24-1-2-8‎ ‎6.如图24-1-2-9，要把破残的圆片复制完整，已知弧上三点A、B、C.‎ ‎(1)用尺规作图法，找出弧BAC所在圆的圆心O；(保留作图痕迹，不写作法)‎ ‎(2)设△ABC为等腰三角形，底边BC=10 cm，腰AB=6 cm，求圆片的半径R；(结果保留根号)‎ ‎(3)若在(2)题中的R满足n＜R＜m(m、n为正整数)，试估算m和n的值.‎ ‎ 图24-1-2-9‎ ‎7.⊙O的直径为10，弦AB的长为8，P是弦AB上的一个动点，求OP长的取值范围.‎ 思路分析：求出OP长的最小值和最大值即得范围，本题考查垂径定理及勾股定理.该题创新点在于把线段OP看作是一个变量，在动态中确定OP的最大值和最小值.事实上只需作OM⊥AB，求得OM即可.‎