九年级下册数学教案 30-4 第3课时 将二次函数问题转化为一元二次方程问题 冀教版

九年级下册数学教案 30-4 第3课时 将二次函数问题转化为一元二次方程问题 冀教版

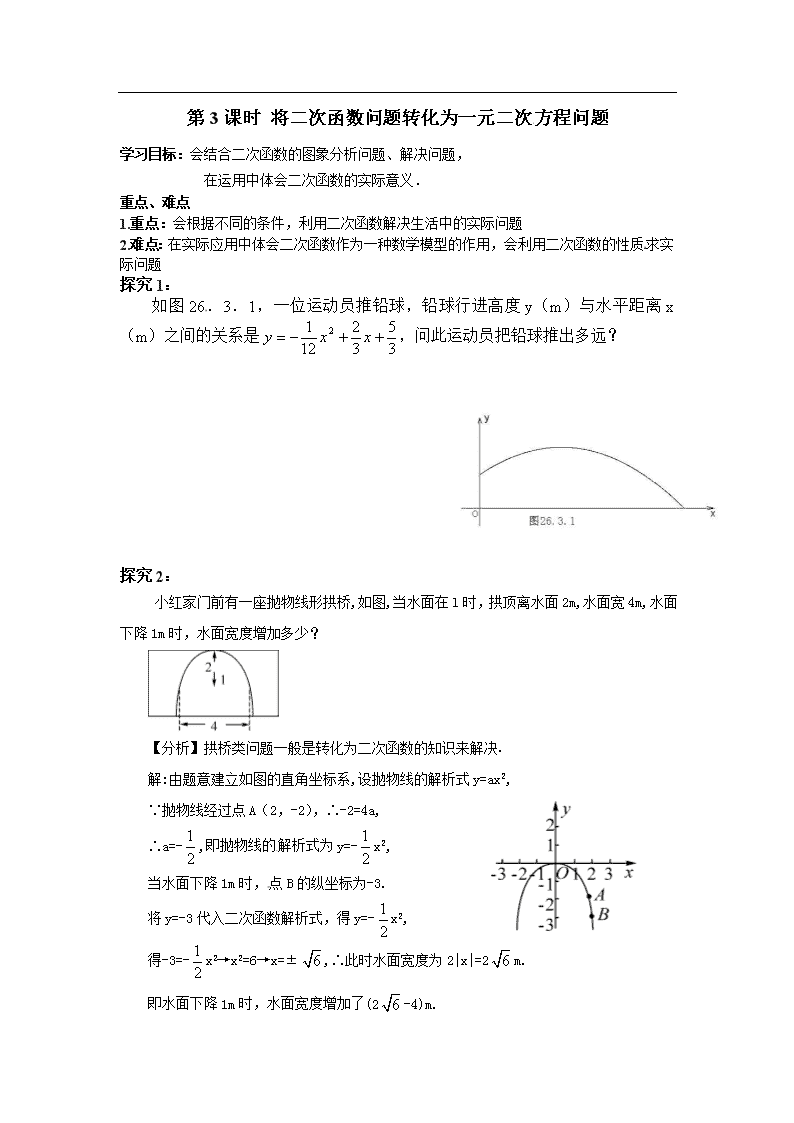
第3课时 将二次函数问题转化为一元二次方程问题 学习目标：会结合二次函数的图象分析问题、解决问题，‎ 在运用中体会二次函数的实际意义．‎ 重点、难点 ‎1.重点：会根据不同的条件，利用二次函数解决生活中的实际问题 ‎2.难点：在实际应用中体会二次函数作为一种数学模型的作用，会利用二次函数的性质求实际问题 探究1：‎ ‎ 如图26．3．1，一位运动员推铅球，铅球行进高度y（m）与水平距离x（m）之间的关系是，问此运动员把铅球推出多远？‎ 探究2：‎ ‎ 小红家门前有一座抛物线形拱桥,如图,当水面在l时，拱顶离水面2m,水面宽4m,水面下降1m时，水面宽度增加多少？‎ ‎【分析】拱桥类问题一般是转化为二次函数的知识来解决.‎ 解:由题意建立如图的直角坐标系,设抛物线的解析式y=ax2,‎ ‎∵抛物线经过点A（2，-2），∴-2=4a,‎ ‎∴a=-,即抛物线的解析式为y=-x2,[来源:学科网]‎ 当水面下降1m时，点B的纵坐标为-3.‎ 将y=-3代入二次函数解析式，得y=-x2,‎ 得-3=-x2→x2=6→x=±,∴此时水面宽度为2|x|=2m.‎ 即水面下降1m时，水面宽度增加了(2-4)m.‎ ‎【自学说明】用二次函数知识解决拱桥类的实际问题一定要建立适当的直角坐标系；抛物线的解析式假设恰当会给解决问题带来方便.‎ 典型例题[来源:学科网]‎ 例1 如图26．3．2，公园要建造圆形的喷水池，在水池中央垂直于水面处安装一个柱子OA，水流在各个方向沿形状相同的抛物线路线落下，为使水流形状较为漂亮，要求设计成水流在离OA距离为1m处达到距水面最大高度2．25m．‎ ‎（1）若不计其他因素，那么水池的半径至少要多少米，才能使喷出的水流不致落到池外？‎ ‎（2）若水流喷出的抛物线形状与（1）相同，水池的半径为3．5m，要使水流不落到池外，此时水流最大高度应达多少米？（精确到0．1m）‎ ‎[来源:学,科,网]‎ 例2 如图，足球场上守门员在O处踢出一高球，球从离地面1米处飞出（A在y轴上），运动员乙在距O点6米的B处发现球在自己的正上方达到最高点M，距地面约4米高，球落地后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.‎ ‎(1)求足球开始飞出到第一次落地时,该抛物线的表达式;‎ ‎(2)足球第一次落地点C距守门员是多少米?(取4≈7,2≈5)[来源:Zxxk.Com]‎ ‎(3)运动员乙要抢到第二个落点D，他应再向前跑多少米？‎ ‎【点拨】由图象的类型及已知条件，设其解析式为y=a(x-6)2+4,过点A（0，1），可求出a;（2）令y=0可求出x的值，x＜0舍去；（3）令y=0,求出C点坐标（6+4,0),设抛物线CND为y=-(x-k)2+2,代入C点坐标可求出k值(k＞6+4).再令y=0可求出C、D的坐标，进而求出BD.‎ 随堂训练 ‎1、河北省赵县的赵州桥的桥拱是抛物线型，建立如图所示的坐标系，其函数的解析式为y=‎ ‎，当水位线在AB位置时，水面宽 AB = 30米，这时水面离桥顶的高度h是（ ） [来源:学科网ZXXK]‎ A、5米 B、6米； C、8米； D、9米[来源:学。科。网]‎ ‎2、、一座抛物线型拱桥如图所示,桥下水面宽度是4m,拱高是2m.当水面下降1m后,水面的宽度是多少?(结果精确到0.1m).‎ ‎3、一个涵洞成抛物线形，它的截面如图,现测得，当水面宽AB＝1.6 m时，涵洞顶点与水面的距离为2.4 m．这时，离开水面1.5 m处，涵洞宽ED是多少？是否会超过1 m？‎ ‎4. 某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.[来源:学科网ZXXK]‎