2012年初三数学延庆一模试题答案

2012年初三数学延庆一模试题答案

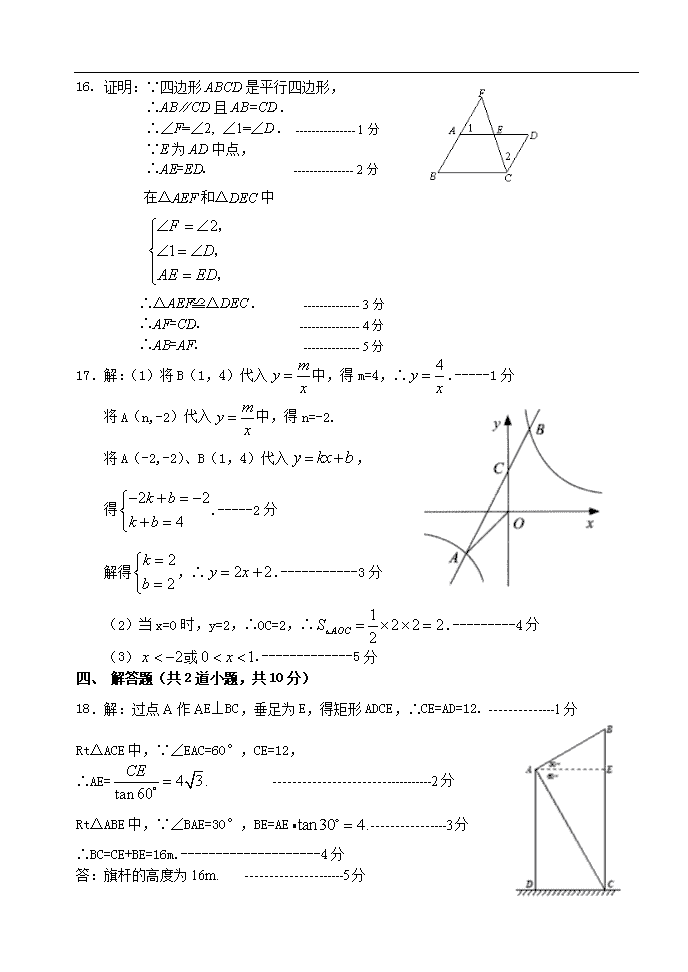
‎2012年延庆县初中毕业试卷 参考答案 一、选择题（共8个小题，每题4分，共32分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 B C D A D ‎ B ‎ ‎ C A 二、填空题（共4个小题，每小题4分，共16分）‎ 题 号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 x≥3‎ a（x+2）（x-2）‎ ‎；‎ 三、解答题（共5道小题，13-17每小题5分，共25分）‎ ‎13． 解：原式 …………………………………………4分 ‎ ． ………………………………………………………5分 ‎14.解：‎ ‎ = ……………………………………2分 ‎ = ……………………………………3分 ‎ ∵=0‎ ‎ ∴ ……………………………………4分 ‎∴原式== ……………………………………5分 ‎15. 解：由①得 ； ……………………………………………2分 由②得 x< 2．……………………………………………… 3分 ‎∴ 此不等式组的解集为．…………………………4分 ‎∴ 此不等式组的整数解为0，1． …………………………5分 ‎16. 证明：∵四边形ABCD是平行四边形，‎ ‎∴AB∥CD且AB=CD．‎ ‎ ∴∠F=∠2, ∠1=∠D． --------------- 1分 ‎∵E为AD中点，‎ ‎∴AE=ED. --------------- 2分 ‎ 在△AEF和△DEC中 ‎∴△AEF≌△DEC． -------------- 3分 ‎∴AF=CD. --------------- 4分 ‎∴AB=AF. -------------- 5分 ‎ ‎17．解：（1）将B（1，4）代入中，得m=4，∴.-----1分 将A（n,-2）代入中，得n=-2.‎ 将A（-2,-2）、B（1，4）代入，‎ 得.-----2分 解得，∴.-----------3分 ‎（2）当x=0时，y=2，∴OC=2，∴.---------4分 ‎（3）或.-------------5分 四、 解答题（共2道小题，共10分）‎ ‎18．解：过点A作AE⊥BC，垂足为E，得矩形ADCE，∴CE=AD=12. --------------1分 Rt△ACE中，∵∠EAC=60°，CE=12，‎ ‎∴AE=. ----------------------------------2分 Rt△ABE中，∵∠BAE=30°，BE=AE.----------------3分 ‎∴BC=CE+BE=‎16m.--------------------4分 答：旗杆的高度为‎16m. ---------------------5分 ‎19. （1）证明：连接OE，-----------------------1分 ‎∵AB=BC且D是BC中点 ‎∴BD⊥AC ‎∵BE平分∠ABD ‎∴∠ABE=∠DBE ‎∵OB=OE ‎∴∠OBE=∠OEB ‎∴∠OEB=∠DBE ‎∴OE∥BD ∴OE⊥AC ‎∴AC与⊙O相切--------------------2分 ‎（2）∵BD=6，sinC=，BD⊥AC ‎∴BC=10 -----------------------------------3分 ‎∴AB=10‎ 设⊙O 的半径为r，则AO=10-r ‎∵AB=BC ∴∠C=∠A ‎∴sinA=sinC=‎ ‎∵AC与⊙O相切于点E，‎ ‎∴OE⊥AC ‎∴sinA===------------------------------------------4分 ‎∴r= ------------------------------------------------------5分 五、解答题（本题满分6分）‎ ‎20．解：⑴A组的户数是：‎ ‎（10÷5）×1=2 ……………………………………1分 调查样本的容量是:‎ ‎（10+2）÷（1-40%-28%-8%）=50 ……………………………………2分 ‎⑵ C组的户数是：50×40%=20 ……………………………………3分 并补全直方图（略） ……………………………………4分 ‎⑶估计捐款不少于300元的户数是：500×（28%+８%）=180户……………6分 六、解答题（共2道小题，共9分）‎ ‎21.解：设原来每天加固x米，根据题意，得……………………………………1分 ‎． ……………………………………2分 去分母，得 1200+4200=18x（或18x=5400）‎ 解得 ． ……………………………………3分 检验：当时，（或分母不等于0）．‎ ‎∴是原方程的解． ……………………………………4分 答：该地驻军原来每天加固‎300米． ……………………………5分 ‎ 22. （本题满分4分）‎ 解：（1） 12……………………………………………………2分；‎ ‎（2） ……………………………………4分。‎ 七、解答题（本题满分7分）‎ ‎23.解： （1） A(1,0)、 …………………………2分（写对一个给1分）；‎ ‎（2）m=1(或解析式)………………………………3分 ‎ 当0 DE 即：BD+DC>AD ------------------- 3分 ‎（2）BD+DC≥AD ---------4分 ‎（3）猜想1：BD+DC〈2AD 证明：把绕点A顺时针旋转，得到 则有, DC=EB，∠ACD=∠ABE ---------5分 ‎∵∠BAC+∠BDC=180 º∴∠ABD+∠ACD=180 º ‎∴∠ABD+∠ABE=180 º 即：E、B、D三点共线---------6分 ‎∵AD=AE, 在中∵AE+AD>DE ‎ 即BD+DC〈2AD ---------------------7分 或者猜想2：‎ ‎ -------------7分 说明：如有不同解法，参照给分。‎ 九、解答题（本题满分8分）‎ ‎25.解：（1）二次函数y1=-x2+3x …………………………………………1分 ‎ B(3，0) …………………………………………2分 ‎（2）由已知可得C(6,0)‎ 如图：过A点作AH⊥x轴于H点，‎ 可得：△OPD∽△OHA ‎∴‎ ‎∴PD=‎2a…………………………………………3分 ‎∵正方形PDEF ‎∴E（‎3a，‎2a）‎ ‎∵E（‎3a，‎2a）在二次函数y1=-x2+3x的图像上 ‎∴ ………………………………………………4分 （3） ‎（每个t值1分，共4分）……………………8分 具体分析：‎ 如图1：当点F、点N重合时，有OF+CN=6，则有 如图2：当点F、点Q重合时，有OF+CQ=6，则有 如图3：当点P、点N重合时，有OP+CN=6，则有 如图4：当点P、点Q重合时，有OP+CQ=6，则有