（鄂尔多斯专版）中考数学复习：关于角平分线的联想课件-36张

（鄂尔多斯专版）中考数学复习：关于角平分线的联想课件-36张

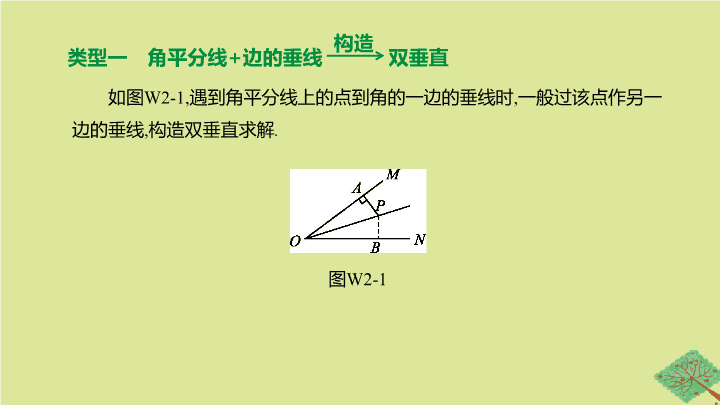
关于角平分线的联想 第四单元　三角形 当题中出现角平分线或易得到角平分线 ( 有对称或等腰三角形 ) 时 , 首先考虑利用角平分线定理求解 . 若另有平行或垂直等条件 , 则可考虑构造等腰三角形或对称图形求解 . 类型一　角平分线 + 边的垂线 双垂直 　　 如图 W2-1, 遇到角平分线上的点到角的一边的垂线时 , 一般过该点作另一边的垂线 , 构造双垂直求解 . 构造 图 W 2 -1 1 . 如图 W2-2,Rt△ ABC 中 , ∠ C =90°, ∠ ABC 的平分线 BD 交 AC 于点 D , 若 CD =3, 则点 D 到 AB 的距离 DE 是 ( 　　 ) A . 5 B . 4 C . 3 D . 2 图 W 2 - 2 C 2 . 如图 W2-3, 在 △ ABC 中 , AB =10, AC =8, ∠ BAC =45°, AD 是∠ BAC 的平分线 , DE ⊥ AB 于点 E , 则 DE 的长是 　　　　 .  图 W2-3 3 . 如图 W2-4, 在平面直角坐标系中 , 矩形 OABC 的顶点 A 在 x 轴的正半轴上 , 顶点 C 在 y 轴的正半轴上 , OA =12, OC =9, 连接 AC. (1) 填空 : 点 B 的坐标为 　　　　 ; AC 的长度为 　　　　 .  (2) 若 CD 平分∠ ACO , 交 x 轴于点 D , 求直线 CD 的函数表达式 . 图 W2-4 解 :(1)(12,9);15 图 W2-4 3 . 如图 W2-4, 在平面直角坐标系中 , 矩形 OABC 的顶点 A 在 x 轴的正半轴上 , 顶点 C 在 y 轴的正半轴上 , OA =12, OC =9, 连接 AC. (2) 若 CD 平分∠ ACO , 交 x 轴于点 D , 求直线 CD 的函数表达式 . 类型二　角平分线 + 角平分线的垂线 等腰三角形 构造 图 W2-5 如图 W2-5, 当题目中有垂直于角平分线的线段 PA 时 , 通过延长 AP 交 ON 于点 B , 构造等腰三角形 AOB 求解 . 4 . 如图 W2-6, 在 △ ABC 中 , ∠ C =90°, AC = BC , AD 平分∠ BAC , BD ⊥ AD , 若 BD =2, 则 AE = 　　　　 .  图 W2-6 [ 答案 ] 4 　 [ 解析 ] 延长 BD , AC 交于点 F , ∵ AD 平分∠ BAC , AD ⊥ BD , ∴∠ ABF = ∠ AFB , BD = FD , BF =2 BD. ∵ AD ⊥ BD , ∠ ACB =90°, ∠ AEC = ∠ BED , ∴∠ EAC = ∠ FBC. 又∵ AC = BC , ∴ △ ACE ≌△ BCF , ∴ AE = BF =2 BD =4 . 5 . 如图 W2-7,△ ABC 中 , ∠ BAC =90°, S △ ABC =10, AD 平分∠ BAC , 交 BC 于点 D , BE ⊥ AD 交 AD 延长线于点 E , 连接 CE , 则 △ ACE 的面积为 　　　　 .  图 W2-7 [ 答案 ] 5 图 W2-8 类型三　见角平分线作对称 全等三角形 构造 图 W2-9 如图 W2-9, 若 P 是∠ MON 平分线上一点 , 点 A 是边 OM 上任意一点 , 可考虑在边 ON 上截取 OB = OA , 连接 PB , 构造 △ OPB ≌△ OPA , 进而将一些线段和角进行等量代换 , 这是常用的解题技巧之一 . 证明 : ∵四边形 ABCD 是菱形 , ∴ BC = CD , CA 平分∠ BCD. ∴∠ BCE = ∠ DCE. ∵ CE = CE , ∴ △ BCE ≌△ DCE. ∴∠ CBE = ∠ CDE. 又∵ AB ∥ DC , ∴∠ APD = ∠ CDE. ∴∠ APD = ∠ CBE. 7 . 如图 W2-10, 在菱形 ABCD 中 , P 是 AB 上的一个动点且不与 A , B 重合 , 连接 DP 交对角线 AC 于 E , 连接 BE. 求证 : ∠ APD = ∠ CBE. 图 W2-10 8 . 如图 W2-11, 在 △ ABC 中 , ∠ C =2 ∠ B , AD 平分∠ BAC , 求证 : AB = AC + CD. 图 W2-11 类型四　角平分线 + 平行线 等腰三角形 　　 当题中同时出现角平分线和平行线时 , 注意找等腰三角形 . 一般地 , 角平分线、平行线、等腰三角形中任意两个条件存在 , 可得第三个条件 . 如图 W2-12, OP 平分∠ MON , PQ ∥ ON , 则 △ OPQ 为等腰三角形 . 图 W2-12 构造 9 . 如图 W2-13, AB ∥ CD , AD 平分∠ BAC , 且∠ C =80°, 则∠ D 的度数为 ( 　　 ) A . 50° B . 60° C . 70° D . 100° 图 W2-13 A 10 . 在 △ ABC 中 , D , E 分别是边 AC , AB 的中点 , 连接 BD. 若 BD 平分∠ ABC , 则下列结论错误的是 ( 　　 ) A .BC =2 BE B . ∠ A = ∠ EDA C .BC =2 AD D .BD ⊥ AC C 11 . 如图 W2-14, AC 是正方形 ABCD 的对角线 , ∠ DCA 的平分线交 BA 的延长线于点 E , 若 AB =3, 则 AE = 　　　　 .  图 W2-14 12 . 在▱ ABCD 中 , AE 平分∠ BAD 交边 BC 于点 E , DF 平分∠ ADC 交边 BC 于点 F , 若 AD =11, EF =5, 则 AB = 　　　　 .  [ 答案 ]8 或 3 [ 解析 ] ①如图① , 在▱ ABCD 中 , ∵ BC ∥ AD , ∴∠ ADF = ∠ CFD. ∵ DF 平分∠ ADC 交 BC 于点 F , ∴∠ ADF = ∠ CDF , ∴∠ CFD = ∠ CDF , ∴ CF = CD. 同理可证 AB = BE. ∴ AB = BE = CF = CD. ∵ EF =5, BC = AD =11, ∴ BC = BE + CF - EF =2 AB - EF =2 AB -5=11, ∴ AB =8 . ②如图② , 在▱ ABCD 中 , 同①可得 AB = BE = CF = CD , ∵ EF =5, ∴ BC = BE + CF + EF =2 AB + EF =2 AB +5=11, ∴ AB =3 . 故答案为 8 或 3 . ① ② 13 . 如图 W2-15, 在 △ ABC 中 , AD 平分∠ BAC , BD ⊥ AD , 过 D 作 DE ∥ AC , 交 AB 于 E , 若 AB =5, 则 DE = 　　　　 .  图 W2-15 14 . 如图 W2-16, 在 △ ABC 中 , CD 平分∠ ACB 交 AB 于 D , DE ∥ AC 交 BC 于点 E , DF ∥ BC 交 AC 于点 F. 求证 : 四边形 DECF 是菱形 . 图 W2-16 证明 : 如图 , ∵ DE ∥ AC , DF ∥ BC , ∴四边形 DECF 为平行四边形 , ∠ 2= ∠ 3 . 又∵ CD 平分∠ ACB 交 AB 于点 D , ∴∠ 1= ∠ 2, ∴∠ 1= ∠ 3, ∴ DE = EC , ∴四边形 DECF 为菱形 . 15 . 如图 W2-17, 在 △ ABC 中 , AB>AC , E 为 BC 边的中点 , AD 为∠ BAC 的平分线 , 过 E 作 AD 的平行线 , 交 AB 于 F , 交 CA 的延长线于点 G. 求证 : BF = AC + AF. 图 W2-17 类型五　角平分线 + 角平分线 三角形内心 图 W2-18 构造 16 . 如图 W2-19 所示 ,△ ABC 的三边 AB , BC , CA 的长分别是 20,30,40, 三条角平分线将 △ ABC 分为三个三角形 , 则 S △ OAB ∶ S △ OBC ∶ S △ OAC = 　　 　　 .  图 W2-19 2 ∶ 3 ∶ 4 17 . 如图 W2-20 所示 , 已知 △ ABC 的周长是 18 cm, BO , CO 分别平分∠ ABC 和∠ ACB , OD ⊥ BC 于点 D , 若 △ ABC 的面积为 45 cm 2 , 则 OD = 　　　　 ; 若∠ BOC =110°, 则∠ A = 　　　　 ° .  图 W2-20 5 cm 40 图 W2-21 [ 答案 ]C