- 2021-11-06 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版九年级上册第六章反比例函数反比例函数习题精选 (40道)(无答案 )
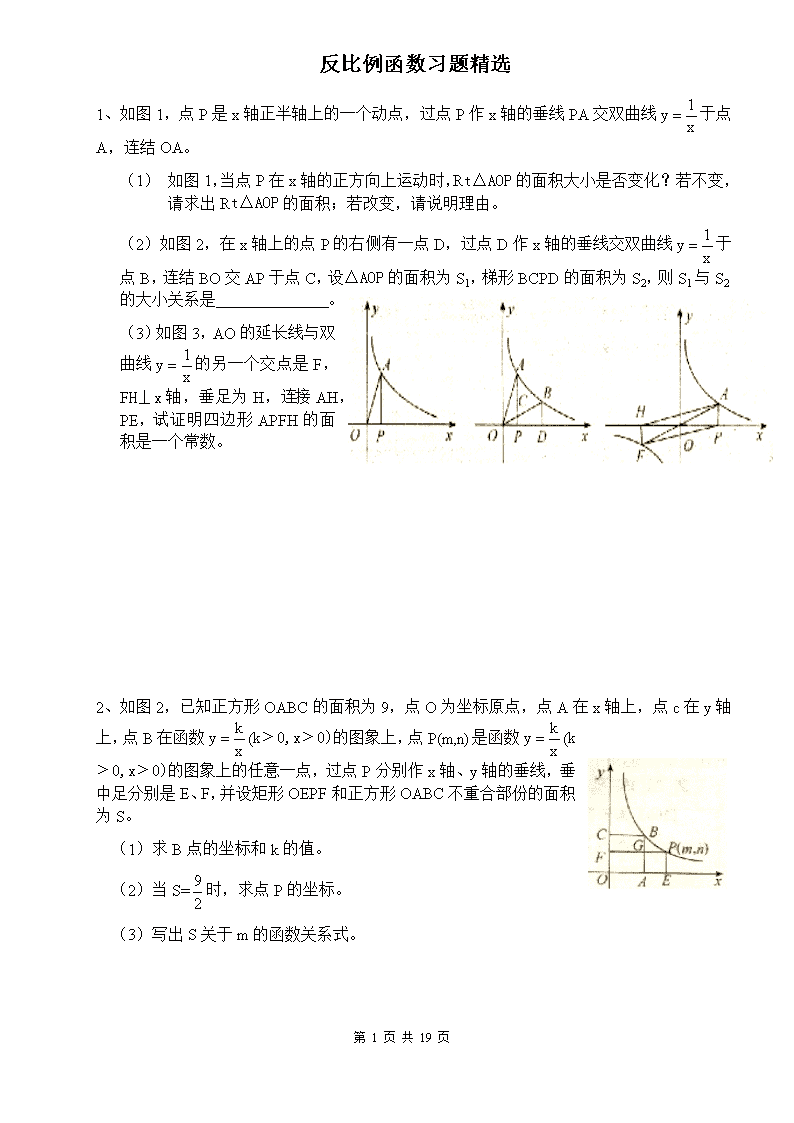
第 1 页 共 12 页 反比例函数习题精选 1、如图 1,点 P是 x轴正半轴上的一个动点,过点 P作 x轴的垂线 PA交双曲线 x 1y 于点 A,连结 OA。 (1) 如图 1,当点 P在 x轴的正方向上运动时,Rt△AOP 的面积大小是否变化?若不变, 请求出 Rt△AOP 的面积;若改变,请说明理由。 (2)如图 2,在 x轴上的点 P的右侧有一点 D,过点 D作 x轴的垂线交双曲线 x 1y 于 点 B,连结 BO 交 AP于点 C,设△AOP 的面积为 S1,梯形 BCPD的面积为 S2,则 S1与 S2 的 大 小 关 系 是 。 (3)如图 3,AO的延长线与双 曲线 x 1y 的另一个交点是 F, FH⊥x 轴,垂足为 H,连接 AH, PE,试证明四边形 APFH 的面 积是一个常数。 2、如图 2,已知正方形 OABC的面积为 9,点 O为坐标原点,点 A在 x轴上,点 c在 y轴 上,点 B在函数 x ky (k﹥0,x﹥0)的图象上,点 P(m,n)是函数 x ky (k﹥0,x﹥0)的图象上的 任意一点,过点 P分别作 x轴、y轴的垂线,垂中足分别是 E、F,并 设矩形 OEPF和正方形 OABC不重合部份的面积为 S。 (1)求 B点的坐标和 k的值。 (2)当 S= 2 9 时,求点 P的坐标。 (3)写出 S关于 m的函数关系式。 第 2 页 共 12 页 3、如图 3,直线 2x 2 1 分别交 x、y轴于点 A、C,P是该直线上在第一象限内的一点,PB ⊥x 轴,B为垂足,S△ABP=9。 (1)求点 P的坐标。 (2)设点 R与点 P在同一反比例函数的图象上,且点 R在直线 PB的右侧,作 RT⊥x 轴,T 为垂足,当△BRT 和△AOC 相似时, 求点 R的坐标。 4、如图 4,一次函数 y=kx+b的图象与反比例函数 x my 的图 象交于 A、B两点。 (1)利用图中条件,求反比例函数和一次函数的解析式; (2)根据图象写出使一次函数的值大于反比例函数的值的 x 的取值范围。 5、如图 5,已知一次函数 y=-x+8和反比例函数 y= x k (k≠0) 的图象在第一象限内有两个不同的公共点 A、B。 (1)求实数 k的取值范围。 (2)若△AOB 的面积为 24,求 k的值。 6、已知如图 6,反比例函数 x 8y 与一次函数 y=-x+2的图象交于 A、B两点,求: (1)A、B两点的坐标。 (2)求△AOB 的面积。 第 3 页 共 12 页 7、如图 7,一次函数的图象经过一、二、三象限,且与反比例函数的图象交于 A、B两点, 与 y轴交于点 C,与 x轴交于点 D,OB= 10 ,tan∠DOB = 3 1 。 (1)求反比例函数的解析式; (2)设点 A的横坐标为 m,△DOB 的面积为 S,求 S 与 m的函数关系式,并写出自变量 m的取值范围。 8、如图 8,双曲线 x 5y 在第一象限的一分支上有一点 C(1,5), 过点 C的直线 y=-kx+b(k﹥0)与 x轴交于点 A(a,0).(1)求点 A 的横坐标与 k之间的函数关系式;(2)当该直线与双曲线在第一 象限内的另一个交点 D的横坐标为 9,求△COD的面积。 9、如图,在 Rt△ABO 的顶点 A是双曲线 x ky 与直线 y=-x-(k+1) 在第二象限的交点,AB⊥x轴于点 B,且 S△ABO= 2 3 。 (1)求这两个函数的解析式; (2)求直线与双曲线的两个交点 A、C的坐标和△AOC 的面积。 第 4 页 共 12 页 10、如图,已知正方形 ABCD,AB=2,P是 BC边上与 B、C不重合的任意一点,DQ⊥AP 于 Q,当点 P在 BC边上移动时,线段 DQ也随着变化,设 PA=x, QD=y,求 y与 x之间的函数关系式。并指出变量的取值范围。 11、如图 11,已知 C,D两点是双曲线 x my 在第一象限内的分支上的两点,直线 CD分别 交 x 轴、y 轴于 A,B 两点,设 C、D 的坐标分别是(x1,y1), (x2,y2)连接 OC、OD。 (1)求证 y1 ﹤OC﹤y1+ 1y m ; (2)若∠BOC=∠AOD=∂,tan∂= 3 1 ,OC= 10 ,求 直线 CD的解析式; (3)在(2)的条件下,双曲线上是否存在一点 P,使得 S △POC=S△POD,若存在,请给出证明;若不存在,请说明理由。 12、如图 12,直线 y=kx+4与函数 x my (x﹥0,m﹥0的图象交于 点 A、B,且与 x,y轴分别交于 C,D两点。 (1)若△COD 的面积是△AOB 的面积的 2倍,求 k与 m之间 的函数关系式; (2)在(1)条件下,是否存在 k和 m,使得对于点(2,0),有 ∠APB=90°,若存在,求出 k和 m的值;若不存在,请说明理 由。 第 5 页 共 12 页 13、如图 13,Rt△ABO的顶点A是双曲线 x ky 与直线 y=-x+(k+1) 在第四象限的交点,AB⊥x 轴于 B,且 S△ABO= 2 3 。 (1)求这两个函数的解析式; (2)求直线与双曲线的两个交点 A,C的坐标和△AOC 的面积。 14、已知反比例函数 x ky 和一次函数 y=-x-6。 (1)若它们的图象交于点(-3,m),求 m和 k的值; (2)当 k满足什么条件时,这两个函数的图象有两个不同的交点? (3)当 k=-2时,设(2)中的两个函数图象的交点分别为 A,B,试判断,A,B两点分 别在第几象限?∠AOB是锐角还是钝角?(直接写出结论) 15、若反比例函数的图象经过点(1,3)。 (1)求反比例函数的解析式; (2)求一次函数 y=2x+1与反比例函数图象的两个交点及原点所围成的三角形的面积。 16、如图 16,点 A、B在反比例函数 x ky 的图象上,且点 A、B的横坐标分别为 a, 2a(a﹥0),AC⊥x 轴,垂足为点 C,且△AOC的面积为 2。 (1)求该反比例函数的解析式; (2)若点(-a,y1),(-2a,y2)在该反比例函数的图象上,试 比较 y1,y2的大小; (3)求△AOB的面积。 第 6 页 共 12 页 17、如图 17,正比例函数 y=kx(k﹥0)与反比例函数 x 4y 的图象 相交于 A、C两点,过 A作 x轴的垂线,交 x轴于点 B,过 C作 x轴的垂线,交 x轴于点 D,试问:当 k取不同数值时,四边形 ABCD的面积有何变化? 18、如图 18,已知反比例函数 x ky 的图象经过点 A( 3 ,b),过点 A作 AB⊥x 轴于点 B,△AOB的面积为 3。 (1)求 k和 b的值; (2)若一次函数 y=ax+1的图象经过点 A,并且与 x轴相交 于点M,求 AO:AM的值。 19、如图 19,已知函数 x 4y 的图象和两条直线 y=x,y=2x 在第 一象限内,分别交于 P1和 P2两点,过 P1分别作 x轴、y轴的垂线 P1Q1、P1R1,垂足分别为 Q1、R1;过 P2分别作 x轴,y 轴的垂线 P2Q2、P2R2,垂足分别为 Q2,R2,求矩形 OQ1P1R1和 OQ2P2R2 的周长,并比较它们的大小及说出这个规律。 20、如图 20,直线 y=k1x+b与双曲线 y= x k 2 只有一个交点 A(1,2), 且与 x轴、y轴分别交于 B,C两点,AD垂直平分 OB,垂足为 D, (1)求直线与双曲线的解析式。(2)A为 BC的中点。 第 7 页 共 12 页 21、如图 21,△AOC的面积为 6,且 CB:BA=3:1,求过点 A的双曲线的表达式。 22、已知反比例函数 y= x 12 的图象和一次函数 y=kx-7的图象都经过点 P(m,2). (1)求这个一次函数的解析式; (2)如果等腰梯形 ABCD 的顶点 A、B在这个一次函数的图象上,顶点 C、D在这个反 比例函数的图象上,两底 AD、BC 与 y轴平行且 A 与 B的横坐标分别为 a 和 a+2,求 a 的 值。 23、如图 23,直线 AB 过点 A(m,0)、B(0,n)(m﹥0,n﹥0)。反比例函数为 x my 的图象与 AB 交于 C、D 两点。P 为双曲线 x my 上任意一点,过 P 作 PQ⊥x 轴于 Q,PR⊥y轴于 R,请分别解答下列问题: (1)若 m+n=10,n为何值时的△AOB的面积最大?最大值是 多少? (2)若 S△AOC=S△OCD=S△ODB,求 n的值。 24、如图 24,两条双曲线在第一象限内,A(1,6),B(a,2),C (b,2),D(a,6)。连结 AB、BC、CD、DA, (1)求 B、C、D三点的坐标; (2)求四边形 ABCD的面积。 第 8 页 共 12 页 25、如图,直线 y=-x+1 与 x轴交于点 A,与 y轴交于点 B,P(a,b)为双 曲线 (x x2 1y 0)上的一点,PM⊥x 轴于M,交 AB于 E,PN⊥y 轴于 N,交 AB于 F。 (1)求△EOF的面积(用 a,b的代数式表示); (2)△EOF和△BOE是否相似?如果相似,请予以证明;如果不相似, 简要说明理由。 26、如图,在直角坐标系中,直线 y=ax+b与双曲线 )0(k x ky 在第一象限交于点 A(2,m),与 x 轴交 于点 C,AB⊥x 轴于 B,且 S△AOB=3,若△ABC 的面积是△ AOB的面积的 2倍,求双曲线和直线的解析式。 27、已知反比例函数 x2 ky 和一次函数 y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。 (1)求反比例函数的解析式; (2)若点 A在第一象限,且同时在上述两个函数的图象上,求点 A的坐标; (3)利用(2)的结果,请问:在 x轴上是否存在点 P,使△AOP 为等腰三角形?若存在,求出符合条 件的点 P的坐标;若不存在,请说明理由。 第 9 页 共 12 页 28、如图,直线 y=2x与双曲线 x 8y 相交于点 A、E,直线 AB与 双曲线交于另一点 B(m,n),与 x轴、y轴分别交于点 C、D,且 m=2n。 直线 EB交 x轴于点 F。 (1)求 A、B两点的坐标; (2)请判断△COD和△CBF是否相似?并说明理由。 29、如图 1,在 Rt△ABC中,∠C=90°,AC=12,BC=5,点M在 AB边上,且 AM=6。 (1)动点 D在 AC边上运动,且与点 A、C均不重合,设 CD=x。 ①设△ABC 与△ADM的面积之比为 y,求 y与 x之间的函 数关系式,并写出自变量的取值范围; ②当 x取何值时,△ADM是等腰三角形?说明你的理由。 (2)如图 2所示,以如图 1中的 BC、CA为一组邻边的矩 形 ACBE 中,动点 D在矩形边上运动一周,能使△ADM是以 ∠AMD为顶角的等腰三角形共有几个?(直接写出结果即可) 第 10 页 共 12 页 30、设 a,b 是关于 x 的方程 kx2+2(k-3)x+(k-3)=0 的两个不相等的实数根(k 是非负整数),一次函数 y=(k-2)x+m与反比例函数 x ny 的图象都经过点(a,b)。 (1)求 k的值; (2)求两个函数的解析式。 31、已知反比例函数 x ky 的图象经过点(4, 2 1 ),若一次函数 y=x+1的图象平移后经过该反比例函数 的图象上的点 B(2,m),求平移后的一次函数的图象与 x轴的交点的坐标。 32、如图,在平行四边形 ABCD 中,AB=8,AD=6,E是 AB边上一个动点,设 AE=x,DE的延长线 交 CB的延长线于 F,设 CF=y,求 y与 x的函数关系式,并求出自变量的取值范围。 33、如图,在平面直角坐标系中,函数 x my (x﹥0,m是常数) 的图象过点 A(1,4),B(a,b),其中 a﹥1,过点 A 作 x 轴的垂线, 垂足为 C,过 B点作 y轴的垂线,垂足为 D,AC交 BD于点 E, 连接 AD、DC、CB。 (1)若△ABD的面积为 4,求点 B的坐标; (2)求证:DC∥AB; (3)当 AD=BC时,求直线 AB的函数解析式。 第 11 页 共 12 页 34、如图,将一块直角三角形纸板的直角顶点放在 C(1, 2 1 )处,两直角边分别与 x,y 轴平 行,纸板的另外两个顶点 A,B 恰好是直线 y=kx+ 2 9 与双曲线 )0(m x my 的交点。 (1)求 m和 k的值; (2)设双曲线 )0(m x my 在 A,B 之间的部份为 L, 让一把三角尺的直角顶点 P 在 L 上滑动,两直角边始 终与坐标轴平行,且与线段 AB 相交于 M,N 两点,请 探究是否存在点 P,使得 MN= 2 1 AB,写出你的探究过程 和结论。 35、“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”,下面是数学 家帕普斯借助函数给出的一种“三等分锐角”的方法(如图所示);将给定的锐角∠AOB 置于 直角坐标系中,边 OB 在 x 轴上,边 OA 与函数 y= x 1 的图象交于 点 P,以 P 为圆心,以 2PO 为半径作弧交反比例函数的图象于 点 R,过点 P作 x轴的平行线,过 R 点作 y 轴的平行线,两直 线相交于点 M,连结 OM 得到∠MOB,则∠MOB= 3 1 ∠AOB,要明白 帕普斯的方法,请研究以下问题: (1)设 P(a, a 1 ),R(b, b 1 ),求直线 OM 对应的函数表达式(用 含 a,b的代数式表示); (2)分别过点 P作 y轴的平行线,过 R作 x轴的平行线,两直线相交于点 Q,请说明 Q点在 直线 OM 上,并据此证明∠MOB= 3 1 ∠AOB。 36、如图所示,矩形 ABCD 在第一象限内且边 BC 在 x 轴上,E 是对角 线 BD 的中点,函数 x ky (k>0,x>0)的图象经过 A、E两点,已知点 A的坐标为(1,3),点 E的纵坐标为 m。 (1)求 k的值; (2)求点 C的横坐标(用 m表示); (3)当∠ABD=45°时,求 m的值。 第 12 页 共 12 页 37、如图,矩形 AOCB 的两边 OC,OA 分别位于 x 轴、y 轴上,点 B 的坐标为( 3 20 - ,5),D 是 AB 边上的一点。将△AOD 沿直线 OD 翻折, 使 A点恰好落在对角线 OB 上的点 E处,若点 E在一反比例函数的图 象上,求该函数的解析式。 38、已知 A(x1,y1),B(x2,y2)是直线 y=-x+2 与双曲线 )0(k x ky 的两个不同的交点。 (1)求 k的取值范围; (2)是否存在这样的 k值,使得(x1-2)(x2-2)= 2 1 1 2 x x x x ?若存在,求出这样的 k值;若不 存在,说明理由。 39、如图,已知点 A(4,m)、B(-1,n)在反比例函数 x 8y 的图象上, 直线 AB 与 x 轴交于点 C,如果点 D在 y轴上,且 DA=DC, (1)求直线 AB 的解析式; (2)求点 D的坐标。 40、如图所示,直线 y=-2x-2 与双曲线 x ky 交于点 A,与 x 轴分别交 于点 B、C,AD⊥x 轴于点 D,如果 S△ADB=S△COB,求 k的值。查看更多