利用相似三角形测高学案5

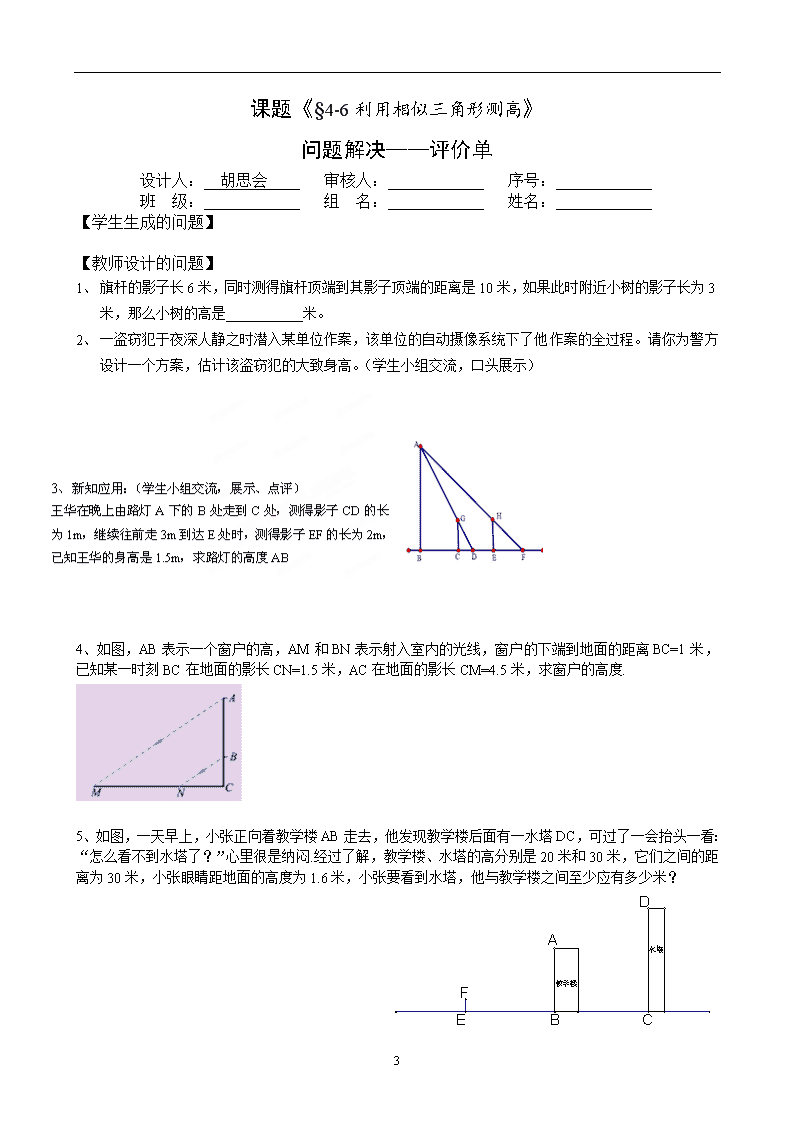
利用相似三角形测高学案5

课题《§4-6利用相似三角形测高》‎ 问题导读——评价单 ‎ 设计人： 胡思会 审核人： 序号： ‎ ‎ 班 级： 组 名： 姓名： ‎ ‎【学习目标】‎ ‎ 学会利用相似三角形的有关知识测量物体的高度，培养学生运用知识解决问题的能力。‎ ‎【重点难点】‎ 重点：三种测量物体高度的方法。‎ 难点：三种方法的选取。‎ ‎【知识链接】‎ 1、 相似三角形的定义：三角 相等，三边 的两个三角形叫做相似三角形。‎ 2、 三角形相似的判定： 。‎ ‎ 。 ‎ ‎ 。 ‎ ‎3、相似三角形的性质：相似三角形的对应角 对应边 。‎ ‎【学法指导】认真阅读课本p103-p104，完成教材中的思考问题（即教材正文加“？”号的地方）解答在教材空白部分；认真完成下列问题，并把自己的疑问列在我的问题处，最后小组交流并解决。‎ 一、利用阳光下的影长测物体的高度 示意图如下图 ‎1、操作方法：一名学生在直立于旗杆影子的顶端处测出该同学的_________和此时旗杆的_______。‎ ‎2、原理：因为太阳离地球非常远，而且太阳的体积比地球大得多，所以可以把太阳光线近似看成平行线，通过平行的太阳光线构造“ ”三角形来测量物高。‎ A E 人影 人 B 物影 物高 C D ‎3、证明 ∵阳光AE 阳光BC，‎ ‎∴∠AEB= ，‎ 又∵∠ABE= =90°‎ ‎∴△ ∽△ ，‎ ‎∴= ，即CD= .‎ ‎4、待测数据： 、 、 。‎ ‎5、结论：同一时刻物高与影长成比例 ‎6、注意：运用此方法时可以把太阳光近似地看成平行光线，计算时还要用到观测者的 。‎ ‎7、若学生身高是1.6m,其影长是2m,旗杆影长5m,求旗杆高度为 。‎ 二、利用标杆测物体的高度 示意图如下 ‎ F E C D H A G B 人 标杆 物高 ‎1、操作方法：选一名学生为观测者，在他和旗杆之间的地面上直立一根高度已知的标杆，观测者前后调整自己的位置，使旗杆顶部、标杆顶部与眼睛恰好在____________时，分别测出他的脚与旗杆底部，以及标杆底部的距离即可求出旗杆的高度。‎ ‎1、原理：人、标杆和旗杆都______于地面，利用光的直线传播通过构造“ ”三角形来测量物高。‎ ‎2、证明：∵ AB CD，‎ ‎∴∠FHD=∠ ，‎ 又∵∠FDH=∠ ，‎ ‎∴△ ∽△ ，‎ 5‎ ‎∴= ，‎ ‎∵FH=EC，ＦＧ＝ＢＥ，EF=HC=GB,DH=DC-HC ,‎ 即= ，AG= .‎ ‎∴物高AB=AG+GB=AG+EF ‎ 3、待测数据： 、 、 、 。‎ ‎4、若学生眼睛距地面高度是1.6m,学生脚距镜子1m,镜子距旗杆底部是5m,求旗杆高度为 。‎ ‎5、运用此方法时观测者的眼睛必须与标杆的顶端和旗杆的顶端“三点共线”，标杆与地面要垂直，在计算时还要用到观测者的眼睛离地面的高度 。‎ 三、利用镜子的反射测物体的高度 示意图如下图 ‎1、操作方法：选一名学生作为观测者．在他与旗杆之间的地面上平放一面镜子，固定镜子的位置，观测者看着镜子来回调整自己的位置，使自己能够通过镜子看到旗杆_______．测出此时他的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度。‎ ‎2、原理：利用光线的入射角等于反射角构造出相似三角形，入射角＝反射角。‎ ‎3、证明：由入射角等于反射角，‎ E射角等于反射角E 人 D C 镜子 阳光 A B 物高 ‎∴∠ =∠ ‎ ‎∵∠ +∠ACB=∠ +∠ ECD =90°‎ ‎∴∠ACB=∠ ， ‎ ‎∵∠ B=∠ D=90°，‎ ‎∴△ ∽△ ，‎ ‎∴= ，即AB= 。‎ ‎4、待测数据： 、 、 。‎ 四、上述三种测量方法各有哪些优缺点？(学生小组交流，口头展示)‎ ‎【法制视窗】‎ 养成良好的饮食习惯：TeX株洲景炎学校欢迎你 一日三餐要吃好，按时定量很必要，早餐吃得好，中餐要吃饱，晚餐精而少；不偏食，不挑食，合理安排很重要；一日三餐有规律，身体强健发育好。吃饭时要做到；细细嚼，慢慢咽，不说笑，不打闹，还要做到吃饭不用汤、水泡。‎ ‎【我的问题】‎ ‎【多元评价】‎ ‎ 自我评价 ‎ ‎ 同伴评价 ‎ 学科长评价 小组长评价 5‎ 课题《§4-6利用相似三角形测高》‎ 问题解决——评价单 ‎ 设计人： 胡思会 审核人： 序号： ‎ ‎ 班 级： 组 名： 姓名： ‎ ‎【学生生成的问题】‎ ‎【教师设计的问题】‎ 1、 旗杆的影子长6米，同时测得旗杆顶端到其影子顶端的距离是10米，如果此时附近小树的影子长为3米，那么小树的高是___________米。‎ 2、 一盗窃犯于夜深人静之时潜入某单位作案，该单位的自动摄像系统下了他作案的全过程。请你为警方设计一个方案，估计该盗窃犯的大致身高。（学生小组交流，口头展示）‎ ‎4、如图，AB表示一个窗户的高，AM和BN表示射入室内的光线，窗户的下端到地面的距离BC=1米，已知某一时刻BC在地面的影长CN=1.5米，AC在地面的影长CM=4.5米，求窗户的高度.‎ ‎5、如图，一天早上，小张正向着教学楼AB走去，他发现教学楼后面有一水塔DC，可过了一会抬头一看：“怎么看不到水塔了？”心里很是纳闷.经过了解，教学楼、水塔的高分别是20米和30米，它们之间的距离为30米，小张眼睛距地面的高度为1.6米，小张要看到水塔，他与教学楼之间至少应有多少米？‎ 5‎ ‎【拓展阅读】泰勒斯与金字塔的高度 ‎ 科学家档案：泰勒斯（公元前624年至前547年），出生在小亚细亚爱奥尼亚西岸的米利都城的一个奴隶主贵族家庭。他年轻时，曾到很多国家游学。回到家乡米利都后，他创办了希腊最早的哲学学派——爱奥尼亚学派，并继续从事哲学、数学、天文学等学科的研究。恩格斯在他的《自然辩证法》中是这样评述泰斯勒的：他是希腊最古老的哲学家、自然科学家、几何学家，是古希腊第一位享有世界声誉，有“科学之父”和“希腊数学的鼻祖”美称的伟大学者。 ‎ ‎ 提起埃及这个古老神秘、充满智慧的国度，人们首先想到的金字塔。金字塔是古埃及国王的陵墓，建于公元前2000多年。古埃及人民仅靠简单的工具，竟能建造出这样雄伟而精致的建筑，真是奇迹！虽历经漫长的岁月，它们如今仍巍峨的送礼者。但是，在金字塔建成的1000多年里，人们都无法测量出金字塔的高度——他们实在太高大了。 ‎ ‎ 约公元前600年，泰勒斯从遥远的希腊来到了埃及。在此之前，他已经到过很多东方国家，学习了各国的数学和天文知识。到埃及后，他学会了土地丈量的方法和规则。他学到的这些知识能够帮助他解决这个千古难题吗？ ‎ ‎ 泰勒斯已经观察金字塔很久了：底部是正方形，四个侧面都是相同的等腰三角形（有两条边相等的三角形）。要测量出底部正方形的边长并不 困难，但仅仅知道这一点还无法解决问题。他苦苦思索着。 ‎ 当他看到金字塔在阳光下的影子时，他突然想到办法了。这一天，阳光的角度很合适，他把他底下的所有东西都拖出一条长长的影子。泰勒斯仔细地观察着影子的变化，找出金字塔地面正方形的一边的中点（这个点到边的两边的距离相等），并作了标记。然后他笔直地站立在沙地上，并请人不断测量他的影子的长度。当影子的长度和他的身高相等时，他立即跑过去的测量金字塔影子的顶点到做标记的中点的距离。他稍做计算，就得出了这座金字塔的高度。 ‎ ‎ 当他算出金字塔高度时，围观的人十分惊讶，纷纷问他是怎样算出金字塔的高度的。泰勒斯一边在沙地上画图示意，一边解释说：“当我笔直地站立在沙地上时，我和我的影构成了一个直角三角形。当我的影子和我的身高相等时，就构成了一个等腰直角三角形。二这时金字塔的高（金字塔顶点到底面正方形中心的连线）和金字塔影子的顶点到底面正方形中心的连线也构成了一个等腰直角三角形。因为这个巨大的等腰直角三角形的两个腰也相等。”他停顿了一下，又说：“刚才金字塔的影子的顶点与我做标记的中心的连线，恰好与这个中点所在的边垂直，这时就很容易计算出金字塔影子的顶点与底面正方形中心的距离了。它等于底面正方形边长的一半加上我刚才测量的距离，算出来的数值也就是金字塔的高度了。” ‎ ‎ 你能理解泰勒斯的计算方法吗？他利用了相似三角形的性质。要知道泰勒斯身处的年代距离现在有2600多年呢！当时人们所了解的科学知识要比现在少得多。泰勒斯因为善于学习，注意观察，勤于思考，终于解决了困惑人们很多年的难题。其实，你在平时的学习种植要注意了这几点，也可以像泰勒斯一样解决很多难题了。 ‎ 5‎ 5‎