2020年山东省济南市平阴县中考数学一模试卷
2020年山东省济南市平阴县中考数学一模试卷
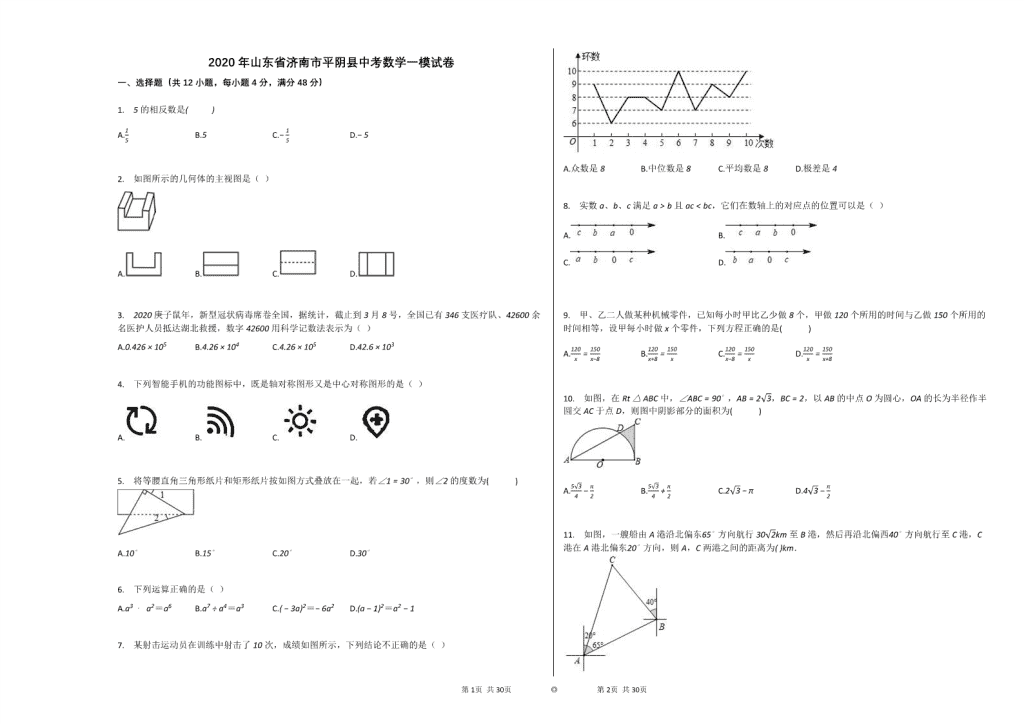
一、选择题(共12小题,每小题4分,满分48分)
1. 5的相反数是( )
A.15 B.5 C.−15 D.−5
2. 如图所示的几何体的主视图是( )
A. B. C. D.
3. 2020庚子鼠年,新型冠状病毒席卷全国,据统计,截止到3月8号,全国已有346支医疗队、42600余名医护人员抵达湖北救援,数字42600用科学记数法表示为( )
A.0.426×105 B.4.26×104 C.4.26×105 D.42.6×103
4. 下列智能手机的功能图标中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5. 将等腰直角三角形纸片和矩形纸片按如图方式叠放在一起,若∠1=30∘,则∠2的度数为( )
A.10∘ B.15∘ C.20∘ D.30∘
6. 下列运算正确的是( )
A.a3⋅a2=a6 B.a7÷a4=a3 C.(−3a)2=−6a2 D.(a−1)2=a2−1
7. 某射击运动员在训练中射击了10次,成绩如图所示,下列结论不正确的是( )
A.众数是8 B.中位数是8 C.平均数是8 D.极差是4
8. 实数a、b、c满足a>b且ac
x−2 ,并写出它的所有整数解.
如图,在▱ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.求证:BF=DE.
某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别
成本价(元/箱)
销售价(元/箱)
甲
25
35
乙
35
48
求:
(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
第29页 共30页 ◎ 第30页 共30页
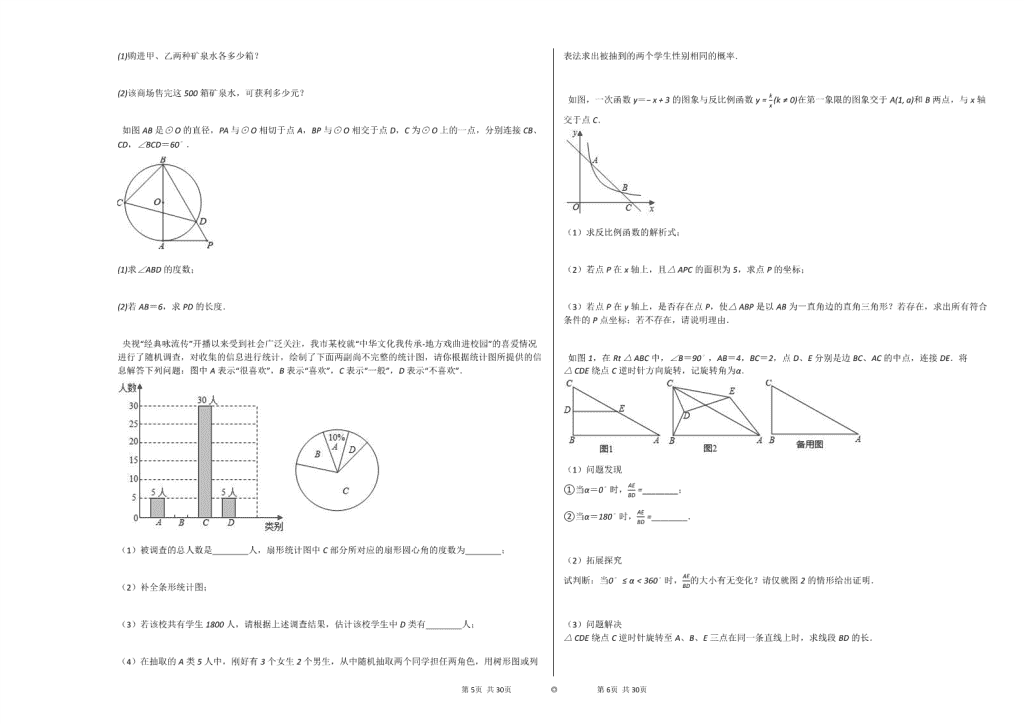
如图AB是⊙O的直径,PA与⊙O相切于点A,BP与⊙O相交于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60∘.
(1)求∠ABD的度数;
(2)若AB=6,求PD的长度.
央视“经典咏流传”开播以来受到社会广泛关注,我市某校就“中华文化我传承-地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图,请你根据统计图所提供的信息解答下列问题:图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是________人,扇形统计图中C部分所对应的扇形圆心角的度数为________;
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中D类有________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
如图,一次函数y=−x+3的图象与反比例函数y=kx(k≠0)在第一象限的图象交于A(1, a)和B两点,与x轴交于点C.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△APC的面积为5,求点P的坐标;
(3)若点P在y轴上,是否存在点P,使△ABP是以AB为一直角边的直角三角形?若存在,求出所有符合条件的P点坐标;若不存在,请说明理由.
如图1,在Rt△ABC中,∠B=90∘,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0∘时,AEBD=________;
②当α=180∘时,AEBD=________.
(2)拓展探究
试判断:当0∘≤α<360∘时,AEBD的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
第29页 共30页 ◎ 第30页 共30页
如图,已知抛物线y=ax2+bx+5经过A(−5, 0),B(−4, −3)两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求△PBC的面积的最大值;
②该抛物线上是否存在点P,使得∠PBC=∠BCD?若存在,求出所有点P的坐标;若不存在,请说明理由.
第29页 共30页 ◎ 第30页 共30页
参考答案与试题解析
2020年山东省济南市平阴县中考数学一模试卷
一、选择题(共12小题,每小题4分,满分48分)
1.
【答案】
D
【考点】
相反数
【解析】
根据相反数的概念解答即可.
【解答】
解:根据相反数的定义有:5的相反数是−5.
故选D.
2.
【答案】
A
【考点】
简单组合体的三视图
【解析】
根据从正面看得到的图形是主视图,可得答案.
【解答】
从正面看是一个矩形中间上面挖去一个矩形,
3.
【答案】
B
【考点】
科学记数法--表示较大的数
【解析】
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【解答】
42600=4.26×104,
4.
【答案】
C
【考点】
轴对称图形
中心对称图形
【解析】
根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.
【解答】
A、不是轴对称图形,是中心对称图形,故本选项错误;
B、是轴对称图形,不是中心对称图形,故本选项错误;
C、既是轴对称图形,也是中心对称图形,故本选项正确;
D、是轴对称图形,不是中心对称图形,故本选项错误.
5.
【答案】
B
【考点】
等腰直角三角形
平行线的性质
【解析】
根据平行线的性质,即可得出∠1=∠ADC=30∘,再根据等腰直角三角形ADE中,∠ADE=45∘,即可得到∠2=45∘−30∘=15∘.
【解答】
解:如图,
∵ AB // CD,
∴ ∠ADC=∠1=30∘.
又∵ 等腰直角三角形ADE中,∠ADE=45∘,
∴ ∠2=45∘−30∘=15∘.
故选B.
6.
【答案】
B
【考点】
幂的乘方与积的乘方
同底数幂的除法
完全平方公式
同底数幂的乘法
【解析】
分别根据同底数幂的乘法法则,同底数幂的除法法则,积的乘方运算法则以及完全平方公式逐一判断即可.
【解答】
A.a3⋅a2=a5,故本选项不合题意;
B.a7÷a4=a3,正确;
C.(−3a)2=9a2,故本选项不合题意;
D.(a−1)2=a2−2a+1,故本选项不合题意.
7.
【答案】
C
第29页 共30页 ◎ 第30页 共30页
【考点】
众数
折线统计图
中位数
算术平均数
极差
【解析】
根据众数、中位数、平均数以及极差的算法进行计算,即可得到不正确的选项.
【解答】
由图可得,数据8出现3次,次数最多,所以众数为8,故A选项正确,不合题意;
10次成绩排序后为:6,7,7,8,8,8,9,9,10,10,所以中位数是:12(8+8)=8,故B选项正确,不合题意;
平均数为110(6+7×2+8×3+9×2+10×2)=8.2,故C选项错误,符合题意;
极差为10−6=4,故D选项正确,不合题意;
8.
【答案】
A
【考点】
数轴
实数
在数轴上表示实数
【解析】
根据不等式的性质,先判断c的正负.再确定符合条件的对应点的大致位置.
【解答】
因为a>b且acb,c<0条件,故满足条件的对应点位置可以是A.
选项B不满足a>b,选项C、D不满足c<0,故满足条件的对应点位置不可以是B、C、D.
9.
【答案】
D
【考点】
由实际问题抽象为分式方程
【解析】
设甲每小时做x个零件,根据甲做120个所用的时间与乙做150个所用的时间相等得出方程解答即可.
【解答】
解:设甲每小时做x个零件,可得:120x=150x+8.
故选D.
10.
【答案】
A
【考点】
求阴影部分的面积
解直角三角形
特殊角的三角函数值
扇形面积的计算
【解析】
根据题意,作出合适的辅助线,即可求得DE的长、∠DOB的度数,然后根据图形可知阴影部分的面积是△ABC的面积减去△AOD的面积和扇形BOD的面积,从而可以解答本题.
【解答】
解:如图,连接OD,过点D作DE⊥AB于点E.
∵ 在Rt△ABC中,
∠ABC=90∘,AB=23,BC=2,
∴ tan∠BAC=BCAB=223=33,
∴ ∠BAC=30∘,
∴ ∠DOB=60∘.
∵ OD=12AB=3,
∴ DE=32,
∴ 阴影部分的面积是:
23×22−3×322−60×π×(3)2360
=534−π2.
故选A.
11.
【答案】
B
【考点】
解直角三角形的应用-方向角问题
【解析】
根据题意得,∠CAB=65∘−20∘,∠ACB=40∘+20∘=60∘,AB=302,过B作BE⊥AC于E,解直角三角形即可得到结论.
【解答】
解:根据题意得,∠CAB=65∘−20∘=45∘,
∠ACB=40∘+20∘=60∘,AB=302,
过B作BE⊥AC于E,
∴ ∠AEB=∠CEB=90∘
第29页 共30页 ◎ 第30页 共30页
,
在Rt△ABE中,∵ ∠ABE=45∘,AB=302,
∴ AE=BE=22AB=30km,
在Rt△CBE中,∵ ∠ACB=60∘,
∴ CE=33BE=103km,
∴ AC=AE+CE=30+103,
∴ A,C两港之间的距离为(30+103)km,
故选B.
12.
【答案】
C
【考点】
一次函数图象上点的坐标特点
含字母系数的二次函数
二次函数图象上点的坐标特征
【解析】
分a>0,a<0两种情况讨论,根据题意列出不等式组,可求a的取值范围.
【解答】
解:∵ 抛物线y=ax2−x+1(a≠0)与线段AB有两个不同的交点,
∴ 令12x+12=ax2−x+1,则2ax2−3x+1=0,
∴ Δ=9−8a>0,
∴ a<98.
①当a<0时,a+1+1≤0,a−1+1≤1,
解得:a≤−2,
∴ a≤−2;
②当a>0时,a+1+1≥0,a−1+1≥1,
解得:a≥1,
∴ 1≤a<98.
综上所述:1≤a<98或a≤−2.
故选C.
二.填空题(共6小题,每小题4分,满分24分)
【答案】
(x+2)2
【考点】
因式分解-运用公式法
【解析】
本题中没有公因式,总共三项,其中有两项能化为两个数的平方和,第三项正好为这两个数的积的2倍,直接运用完全平方公式进行因式分解.
【解答】
x2+4x+4=(x+2)2.
【答案】
1x−2
【考点】
分式的加减运算
【解析】
首先通分,然后根据异分母的分式相加减的法则计算即可.
【解答】
4x2−4+1x+2
=4x2−4+x−2x2−4
=x+2x2−4
=1x−2
【答案】
22
【考点】
列表法与树状图法
【解析】
设袋中黑球的个数为x,利用概率公式得到方程,解方程即可.
【解答】
设袋中黑球的个数为x,
根据题意得55+23+x=110,
解得x=22,
即袋中黑球的个数为22个.
【答案】
8
第29页 共30页 ◎ 第30页 共30页
【考点】
正多边形和圆
【解析】
根据正n边形的中心角是360n即可求解.
【解答】
正多边形的边数是:36045=8.
【答案】
20
【考点】
一次函数的应用
【解析】
根据题意,可知甲乙两地的距离是30km,小王从甲地到乙地用的时间为3h,从而可以求得小王的速度,然后根据图象可知,两人1h时相遇,从而可以求得小李的速度,本题得以解决.
【解答】
由图象可得,
小王的速度为30÷3=10(km/h),
则小李的速度为:30÷1−10=30−10=20(km/h),
【答案】
①④⑤
【考点】
矩形的性质
翻折变换(折叠问题)
【解析】
由折叠的性质,可得∠DMC=∠EMC,CD=CE,∠AMP=∠EMP,AB=GE,由平角的定义可求∠PME+∠CME=12×180∘=90∘,可判断①正确;由折叠的性质可得∠GEC=180∘,可判断②正确;设AB=x,则AD=22x,由勾股定理可求MP和PC的长,即可判断③错误,先求出PB=22x,即可判断④正确,由平行线分线段成比例可求PG=2EF,可判断⑤正确,即可求解.
【解答】
∵ 沿着CM折叠,点D的对应点为E,
∴ ∠DMC=∠EMC,CD=CE,
∵ 再沿着MP折叠,使得AM与EM重合,折痕为MP,
∴ ∠AMP=∠EMP,AB=GE,
∵ ∠AMD=180∘,
∴ ∠PME+∠CME=12×180∘=90∘,
∴ △CMP是直角三角形;故①正确;
∵ 沿着CM折叠,点D的对应点为E,
∴ ∠D=∠MEC=90∘,
∵ 再沿着MP折叠,使得AM与EM重合,折痕为MP,
∴ ∠MEG=∠A=90∘,
∴ ∠GEC=180∘,
∴ 点C、E、G在同一条直线上,故②错误;
∵ AD=22AB,
∴ 设AB=x,则AD=22x,
∵ 将矩形ABCD对折,得到折痕MN;
∴ DM=12AD=2x,
∴ CM=DM2+CD2=3x,
∵ ∠PMC=90∘,MN⊥PC,
∴ CM2=CN⋅CP,
∴ CP=3x22x=322x,
∴ PN=CP−CN=22x,
∴ PM=MN2+PN2=62x,
∴ PCPM=326=3,
∴ PC=3PM,故③错误,
∵ PC=322x,
∴ PB=BC−PC=22x−322x=22x,
∴ BPAB=22xx=22,
∴ BP=22AB,故④正确,
∵ ∠MEC=∠G=90∘,
∴ PG // ME,
∴ CECG=EFPG,
∵ AB=GE=CD=CE,
∴ CG=2CE,
∴ PG=2EF,故⑤正确,
三、解答题:(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤)
【答案】
原式=2+1−2×12+5
=2+1−1+5
=7.
【考点】
零指数幂、负整数指数幂
零指数幂
实数的运算
特殊角的三角函数值
【解析】
第29页 共30页 ◎ 第30页 共30页
直接利用特殊角的三角函数值以及零指数幂的性质、二次根式的性质、负整数指数幂的性质分别化简得出答案.
【解答】
原式=2+1−2×12+5
=2+1−1+5
=7.
【答案】
解不等式①得:x≥1,
解不等式②得:x<4,
所以,原不等式组的解集是1≤x<4,
它的所有整数解有:x=1;x=2;x=3.
【考点】
一元一次不等式组的整数解
解一元一次不等式组
【解析】
分别求出不等式组中两不等式的解集,找出两解集的方法部分确定出不等式组的解集,进而求出整数解即可.
【解答】
解不等式①得:x≥1,
解不等式②得:x<4,
所以,原不等式组的解集是1≤x<4,
它的所有整数解有:x=1;x=2;x=3.
【答案】
证明:∵ 四边形ABCD是平行四边形,
∴ AB // CD,AB=CD,
∴ ∠ABE=∠CDF,
在△ABE和△DCF中,
∠BAE=∠DCFAB=CD∠ABE=∠CDF
∴ △ABE≅△DCF(ASA),
∴ BE=DF,
∴ BE+EF=DF+EF,
即BF=DE.
【考点】
全等三角形的性质与判定
平行四边形的性质
【解析】
欲证明BF=DE,只要证明△ABE≅△DCF即可.
【解答】
证明:∵ 四边形ABCD是平行四边形,
∴ AB // CD,AB=CD,
∴ ∠ABE=∠CDF,
在△ABE和△DCF中,
∠BAE=∠DCFAB=CD∠ABE=∠CDF
∴ △ABE≅△DCF(ASA),
∴ BE=DF,
∴ BE+EF=DF+EF,
即BF=DE.
【答案】
解:(1)设购进甲矿泉水x箱,购进乙矿泉水y箱,
依题意,得:x+y=500,25x+35y=14500,
解得:x=300,y=200.
答:购进甲矿泉水300箱,购进乙矿泉水200箱.
(2)(35−25)×300+(48−35)×200=5600(元).
答:该商场售完这500箱矿泉水,可获利5600元.
【考点】
二元一次方程组的应用——销售问题
【解析】
(1)设购进甲矿泉水x箱,购进乙矿泉水y箱,根据该商场用14500元购进甲、乙两种矿泉水共500箱,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)根据总利润=单箱利润×销售数量,即可求出结论.
【解答】
解:(1)设购进甲矿泉水x箱,购进乙矿泉水y箱,
依题意,得:x+y=500,25x+35y=14500,
解得:x=300,y=200.
答:购进甲矿泉水300箱,购进乙矿泉水200箱.
(2)(35−25)×300+(48−35)×200=5600(元).
答:该商场售完这500箱矿泉水,可获利5600元.
【答案】
解:(1)如图,连接AD.
∵ BA是⊙O直径,
∴ ∠BDA=90∘.
∵ BD=BD,
第29页 共30页 ◎ 第30页 共30页
∴ ∠BAD=∠C=60∘.
∴ ∠ABD=90∘−∠BAD=90∘−60∘=30∘.
(2)∵ AP是⊙O的切线,
∴ ∠BAP=90∘.
在Rt△BAD中,∵ ∠ABD=30∘,
∴ DA=12BA=12×6=3.
∴ BD=3DA=33.
在Rt△BAP中,∵ cos∠ABD=ABPB,
∴ cos30∘=6PB=32.
∴ BP=43.
∴ PD=BP−BD=43−33=3.
【考点】
圆周角定理
切线的性质
【解析】
(1)解法一:要的圆周角定理得:∠ADB=90∘,由同弧所对的圆周角相等和直角三角形的性质可得结论;
解法二:根据同弧所对的圆心角是圆周角的2倍可得∠BOD=120∘,由同圆的半径相等和等腰三角形的性质可得结论;
(2)如图1,根据切线的性质可得∠BAP=90∘,根据直角三角形30∘角的性质可计算AD的长,由勾股定理计算DB的长,由三角函数可得PB的长,从而得PD的长.
【解答】
解:(1)如图,连接AD.
∵ BA是⊙O直径,
∴ ∠BDA=90∘.
∵ BD=BD,
∴ ∠BAD=∠C=60∘.
∴ ∠ABD=90∘−∠BAD=90∘−60∘=30∘.
(2)∵ AP是⊙O的切线,
∴ ∠BAP=90∘.
在Rt△BAD中,∵ ∠ABD=30∘,
∴ DA=12BA=12×6=3.
∴ BD=3DA=33.
在Rt△BAP中,∵ cos∠ABD=ABPB,
∴ cos30∘=6PB=32.
∴ BP=43.
∴ PD=BP−BD=43−33=3.
【答案】
50,216∘
如图所示,总人数为50人,则B的人数=50−5−30−5=10(人);
补全条形统计图如图:
180
设3个女生分别为女1,女2,女3,2个男生分别为男1,男2,所有可能出现的结果如下表:
女1
女2
女3
男1
男2
女1
(女1,女2)
(女1,女3)
(女1,男1)
(女1,男2)
女2
(女2,女1)
(女2,女3)
(女2,男1)
(女2,男2)
女3
(女3,女1)
(女3,女2)
(女3,男1)
(女3,男2)
男1
(男1,女1)
(男1,女2)
(男1,女3)
(男1,男2)
男2
(男2,女1)
(男2,女2)
(男2,女3)
(男2,男1)
从中随机抽取两个同学担任两角色,所有可能的结果有20种,每种结果的可能性都相同,其中,抽到性别相同的结果有8种,
所以P(被抽到的两个学生性别相同)=820=25.
【考点】
列表法与树状图法
扇形统计图
用样本估计总体
第29页 共30页 ◎ 第30页 共30页
条形统计图
【解析】
(1)由A的人数除以所占百分比得出调查的总人数;由360∘乘以C部分所占的比例即可得出C部分所对应的扇形圆心角的度数;
(2)求出B部分的人数,补全条形统计图即可;
(3)由该校总人数乘以D类所占的比例即可得出答案;
(4)由列表法和概率公式即可得出答案.
【解答】
5÷10%=50(人),扇形统计图中C部分所对应的扇形圆心角的度数为360∘×3050=216∘;
故答案为:50; 216∘;
如图所示,总人数为50人,则B的人数=50−5−30−5=10(人);
补全条形统计图如图:
1800×550=180(人);
故答案为:180;
设3个女生分别为女1,女2,女3,2个男生分别为男1,男2,所有可能出现的结果如下表:
女1
女2
女3
男1
男2
女1
(女1,女2)
(女1,女3)
(女1,男1)
(女1,男2)
女2
(女2,女1)
(女2,女3)
(女2,男1)
(女2,男2)
女3
(女3,女1)
(女3,女2)
(女3,男1)
(女3,男2)
男1
(男1,女1)
(男1,女2)
(男1,女3)
(男1,男2)
男2
(男2,女1)
(男2,女2)
(男2,女3)
(男2,男1)
从中随机抽取两个同学担任两角色,所有可能的结果有20种,每种结果的可能性都相同,其中,抽到性别相同的结果有8种,
所以P(被抽到的两个学生性别相同)=820=25.
【答案】
把点A(1, a)代入y=−x+3,得a=2,
∴ A(1, 2),
把A(1, 2)代入反比例函数y=kx,
∴ k=1×2=2;
∴ 反比例函数的表达式为y=2x;
∵ 一次函数y=−x+3的图象与x轴交于点C,
∴ C(3, 0),
设P(x, 0),
∴ PC=|3−x|,
∴ S△APC=12|3−x|×2=5,
∴ x=−2或x=8,
∴ P的坐标为(−2, 0)或(8, 0);
存在,
理由如下:联立y=−x+3y=2x ,
解得:x1=1y1=2 或x1=2y1=1 ,
∴ B点坐标为(2, 1),
∵ 点P在y轴上,
∴ 设P(0, m),
∴ AB=(1−2)2+(2−1)2=2,AP=(1−0)2+(2−m)2,PB=(2−0)2+(1−m)2,
若BP为斜边,
∴ BP2=AB2+AP2 ,
即 ((2−0)2+(1−m)2)2=2+((1−0)2+(2−m)2)2,
解得:m=1,
∴ P(0, 1);
若AP为斜边,
∴ AP2=PB2+AB2 ,
即 ((1−0)2+(2−m)2)2=((2−0)2+(1−m)2)2+2,
解得:m=−1,
∴ P(0, −1);
综上所述:P(0, 1)或 P(0, −1).
【考点】
反比例函数综合题
【解析】
(1)将点A坐标代入两个解析式可求a的值,k的值,即可求解;
(2)设P(x, 0),由三角形的面积公式可求解;
(3)分两种情况讨论,由两点距离公式分别求出AP,AB,BP的长,由勾股定理可求解.
第29页 共30页 ◎ 第30页 共30页
【解答】
把点A(1, a)代入y=−x+3,得a=2,
∴ A(1, 2),
把A(1, 2)代入反比例函数y=kx,
∴ k=1×2=2;
∴ 反比例函数的表达式为y=2x;
∵ 一次函数y=−x+3的图象与x轴交于点C,
∴ C(3, 0),
设P(x, 0),
∴ PC=|3−x|,
∴ S△APC=12|3−x|×2=5,
∴ x=−2或x=8,
∴ P的坐标为(−2, 0)或(8, 0);
存在,
理由如下:联立y=−x+3y=2x ,
解得:x1=1y1=2 或x1=2y1=1 ,
∴ B点坐标为(2, 1),
∵ 点P在y轴上,
∴ 设P(0, m),
∴ AB=(1−2)2+(2−1)2=2,AP=(1−0)2+(2−m)2,PB=(2−0)2+(1−m)2,
若BP为斜边,
∴ BP2=AB2+AP2 ,
即 ((2−0)2+(1−m)2)2=2+((1−0)2+(2−m)2)2,
解得:m=1,
∴ P(0, 1);
若AP为斜边,
∴ AP2=PB2+AB2 ,
即 ((1−0)2+(2−m)2)2=((2−0)2+(1−m)2)2+2,
解得:m=−1,
∴ P(0, −1);
综上所述:P(0, 1)或 P(0, −1).
【答案】
5,5
如图2,
当0∘≤α<360∘时,AEBD的大小没有变化,
∵ ∠ECD=∠ACB,
∴ ∠ECA=∠DCB,
又∵ ECDC=ACBC=5,
∴ △ECA∽△DCB,
∴ AEBD=ECDC=5..
①如图3−1中,当点E在AB的延长线上时,
在Rt△BCE中,CE=5,BC=2,
∴ BE=EC2−BC2=5−4=1,
∴ AE=AB+BE=5,
∵ AEBD=5,
∴ BD=55=5.
②如图3−2中,当点E在线段AB上时,
易知BE=1,AE=4−1=3,
∵ AEBD=5,
∴ BD=355,
综上所述,满足条件的BD的长为355或5.
【考点】
几何变换综合题
【解析】
(1)①当α=0∘时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出的AEBD值是多少.
②α=180∘时,可得AB // DE,然后根据ACAE=BCDB,求出AEBD的值是多少即可.
(2)首先判断出∠ECA=∠DCB,再根据ECDC=ACBC=5
第29页 共30页 ◎ 第30页 共30页
,判断出△ECA∽△DCB,然后由相似三角形的对应边成比例,求得答案.
(3)分两种情形:①如图3−1中,当点E在AV的延长线上时,②如图3−2中,当点E在线段AB上时,分别求解即可.
【解答】
①当α=0∘时,
∵ Rt△ABC中,∠B=90∘,
∴ AC=AB2+BC2=22+42=25,
∵ 点D、E分别是边BC、AC的中点,
∴ AE=12AC=5,BD=12BC=1,
∴ AEBD=5.
②如图1−1中,
当α=180∘时,
可得AB // DE,
∵ ACAE=BCBD,
∴ AEBD=ACBC=5.
故答案为:①5,②5.
如图2,
当0∘≤α<360∘时,AEBD的大小没有变化,
∵ ∠ECD=∠ACB,
∴ ∠ECA=∠DCB,
又∵ ECDC=ACBC=5,
∴ △ECA∽△DCB,
∴ AEBD=ECDC=5..
①如图3−1中,当点E在AB的延长线上时,
在Rt△BCE中,CE=5,BC=2,
∴ BE=EC2−BC2=5−4=1,
∴ AE=AB+BE=5,
∵ AEBD=5,
∴ BD=55=5.
②如图3−2中,当点E在线段AB上时,
易知BE=1,AE=4−1=3,
∵ AEBD=5,
∴ BD=355,
综上所述,满足条件的BD的长为355或5.
【答案】
将点A、B坐标代入二次函数表达式得:25a−5b+5=016a−4b+5=−3 ,解得:a=1b=6 ,
故抛物线的表达式为:y=x2+6x+5…①,
令y=0,则x=−1或−5,
即点C(−1, 0);
①如图1,过点P作y轴的平行线交BC于点G,
第29页 共30页 ◎ 第30页 共30页
将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=x+1…②,
设点G(t, t+1),则点P(t, t2+6t+5),
S△PBC=12PG(xC−xB)=32(t+1−t2−6t−5)=−32t2−152t−6,
∵ −32<0,∴ S△PBC有最大值,当t=−52时,其最大值为278;
②设直线BP与CD交于点H,
当点P在直线BC下方时,
∵ ∠PBC=∠BCD,∴ 点H在BC的中垂线上,
线段BC的中点坐标为(−52, −32),
过该点与BC垂直的直线的k值为−1,
设BC中垂线的表达式为:y=−x+m,将点(−52, −32)代入上式并解得:
直线BC中垂线的表达式为:y=−x−4…③,
同理直线CD的表达式为:y=2x+2…④,
联立③④并解得:x=−2,即点H(−2, −2),
同理可得直线BH的表达式为:y=12x−1…⑤,
联立①⑤并解得:x=−32或−4(舍去−4),
故点P(−32, −74);
当点P(P′)在直线BC上方时,
∵ ∠PBC=∠BCD,∴ BP′ // CD,
则直线BP′的表达式为:y=2x+s,将点B坐标代入上式并解得:s=5,
即直线BP′的表达式为:y=2x+5…⑥,
联立①⑥并解得:x=0或−4(舍去−4),
故点P(0, 5);
故点P的坐标为P(−32, −74)或(0, 5).
【考点】
二次函数综合题
【解析】
(1)将点A、B坐标代入二次函数表达式,即可求解;
(2)①S△PBC=12PG(xC−xB),即可求解;②分点P在直线BC下方、上方两种情况,分别求解即可.
【解答】
将点A、B坐标代入二次函数表达式得:25a−5b+5=016a−4b+5=−3 ,解得:a=1b=6 ,
故抛物线的表达式为:y=x2+6x+5…①,
令y=0,则x=−1或−5,
即点C(−1, 0);
①如图1,过点P作y轴的平行线交BC于点G,
将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=x+1…②,
设点G(t, t+1),则点P(t, t2+6t+5),
S△PBC=12PG(xC−xB)=32(t+1−t2−6t−5)=−32t2−152t−6,
∵ −32<0,∴ S△PBC有最大值,当t=−52时,其最大值为278;
②设直线BP与CD交于点H,
当点P在直线BC下方时,
∵ ∠PBC=∠BCD,∴ 点H在BC的中垂线上,
线段BC的中点坐标为(−52, −32),
过该点与BC垂直的直线的k值为
第29页 共30页 ◎ 第30页 共30页
−1,
设BC中垂线的表达式为:y=−x+m,将点(−52, −32)代入上式并解得:
直线BC中垂线的表达式为:y=−x−4…③,
同理直线CD的表达式为:y=2x+2…④,
联立③④并解得:x=−2,即点H(−2, −2),
同理可得直线BH的表达式为:y=12x−1…⑤,
联立①⑤并解得:x=−32或−4(舍去−4),
故点P(−32, −74);
当点P(P′)在直线BC上方时,
∵ ∠PBC=∠BCD,∴ BP′ // CD,
则直线BP′的表达式为:y=2x+s,将点B坐标代入上式并解得:s=5,
即直线BP′的表达式为:y=2x+5…⑥,
联立①⑥并解得:x=0或−4(舍去−4),
故点P(0, 5);
故点P的坐标为P(−32, −74)或(0, 5).
第29页 共30页 ◎ 第30页 共30页