- 2021-11-06 发布 |
- 37.5 KB |
- 6页

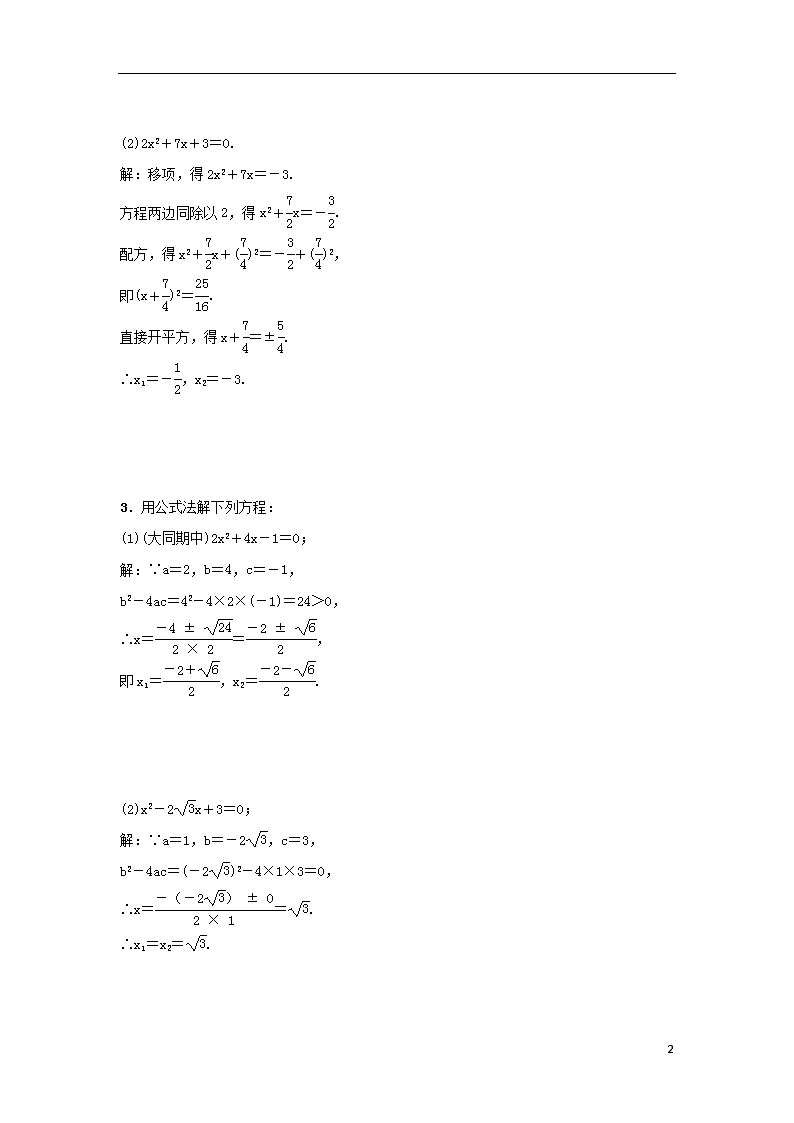

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020九年级数学上册 第二十一章小专题1 一元二次方程的解法习题
小专题1 一元二次方程的解法 1.用直接开平方法解下列方程: (1)3x2-27=0; 解:移项,得3x2=27, 两边同除以3,得x2=9, 根据平方根的定义,得x=±3, 即x1=3,x2=-3. (2)2(3x-1)2=8. 解:方程两边同时除以2,得(3x-1)2=4. 方程两边同时开方,得3x-1=±2. 移项、两边同时除以3,得x1=1,x2=-. 2.用配方法解下列方程: (1)-x2+2x-5=0; 解:移项、系数化为1,得x2-2x=-5. 配方,得x2-2x+1=-5+1, 即(x-1)2=-4. ∴原方程无解. 6 (2)2x2+7x+3=0. 解:移项,得2x2+7x=-3. 方程两边同除以2,得x2+x=-. 配方,得x2+x+()2=-+()2, 即(x+)2=. 直接开平方,得x+=±. ∴x1=-,x2=-3. 3.用公式法解下列方程: (1)(大同期中)2x2+4x-1=0; 解:∵a=2,b=4,c=-1, b2-4ac=42-4×2×(-1)=24>0, ∴x==, 即x1=,x2=. (2)x2-2x+3=0; 解:∵a=1,b=-2,c=3, b2-4ac=(-2)2-4×1×3=0, ∴x==. ∴x1=x2=. 6 (3)x=(x+1)(x-1). 解:将原方程化为一般形式,得x2-x-=0. ∵a=,b=-,c=-, b2-4ac=(-)2-4××(-)=11>0, ∴x==. ∴x1=,x2=. 4.用因式分解法解下列方程: (1)x2-3x=0; 解:x(x-3)=0, ∴x=0或x-3=0. ∴x1=0,x2=3. (2)2(t-1)2+8t=0; 解:原方程可化为2t2+4t+2=0. ∴t2+2t+1=0. ∴(t+1)2=0. ∴t1=t2=-1. (3)(阳泉市平定县月考)x(2x-5)=4x-10; 解:原方程可化为x(2x-5)-2(2x-5)=0. 因式分解,得(x-2)(2x-5)=0. ∴x-2=0或2x-5=0. 6 ∴x1=2,x2=. (4)x2-3x=(2-x)(x-3). 解:原方程可化为x(x-3)=(2-x)(x-3). 移项,得x(x-3)-(2-x)(x-3)=0. ∴(x-3)(2x-2)=0. ∴x-3=0或2x-2=0. ∴x1=3,x2=1. 5.用合适的方法解下列方程: (1)4(x-3)2-25(x-2)2=0; 解:原方程可化为[2(x-3)]2-[5(x-2)]2=0, 即(2x-6)2-(5x-10)2=0. ∴(2x-6+5x-10)(2x-6-5x+10)=0, 即(7x-16)(-3x+4)=0. ∴x1=,x2=. (2)5(x-3)2=x2-9; 解:5(x-3)2=(x+3)(x-3), 移项,得5(x-3)2-(x+3)(x-3)=0. ∴(x-3)[5(x-3)-(x+3)]=0, 即(x-3)(4x-18)=0. ∴x-3=0或4x-18=0. ∴x1=3,x2=. (3)(山西农业大学附中月考)x2-4x=4. 解:原方程可化为x2-2x=4, 6 即x2-2x-4=0. b2-4ac=(2)2-4×1×(-4) =8+16 =24, ∴x=. ∴x1=+,x2=-. 6.我们把称作二阶行列式,规定它的运算法则为=ad-bc.如:=2×5-3×4=-2.如果=6,求x的值. 解:由题意,得(x+1)2-(1-x)(x-1)=6, 解得x1=,x2=-. 7.阅读例题,解答问题: 例:解方程x2-|x|-2=0. 解:原方程化为|x|2-|x|-2=0. 令y=|x|,原方程化成y2-y-2=0. 解得y1=2,y2=-1(不合题意,舍去). ∴|x|=2.∴x=±2. ∴原方程的解是x1=2,x2=-2. 请模仿上面的方法解方程:(x-1)2-5|x-1|-6=0. 解:原方程化为|x-1|2-5|x-1|-6=0. 令y=|x-1|,原方程化成y2-5y-6=0. 解得y1=6,y2=-1(不合题意,舍去). ∴|x-1|=6. ∴x-1=±6. 6 解得x1=7,x2=-5. ∴原方程的解是x1=7,x2=-5. 6查看更多