- 2021-11-06 发布 |
- 37.5 KB |
- 51页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
新人教版九年级数学上册第二十四章圆单元测试卷3套(附答案)
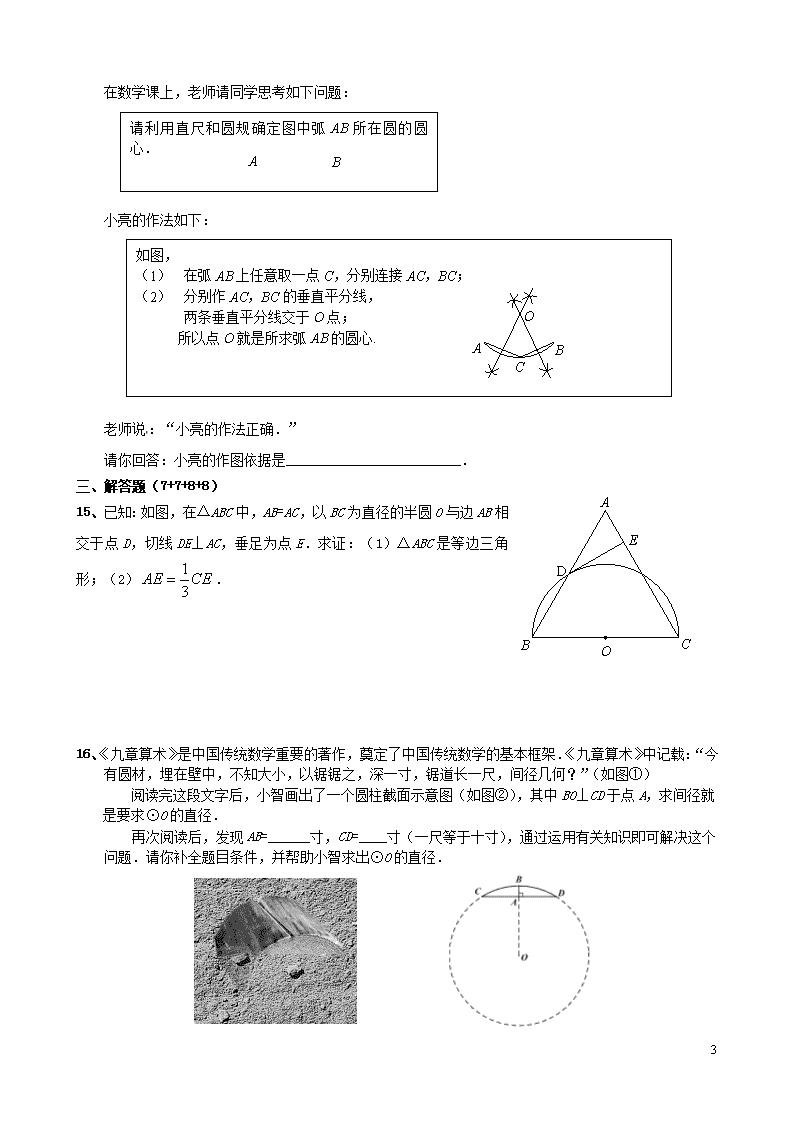
九年级数学上册第二十四章圆单元测试卷1 一、填空题(每题5分,计40分) 1、已知点O为△ABC的外心,若∠A=80°,则∠BOC的度数为( ) A.40° B.80° C.160° D.120° 2.点P在⊙O内,OP=2cm,若⊙O的半径是3cm,则过点P的最短弦的长度为( ) A.1cm B.2cm C.cm D.cm 3.已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,,那么点P与⊙O的位置关系是( ) A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定 4.如图,为的四等分点,动点从圆心出发,沿路线作匀速运动,设运动时间为(s).,则下列图象中表示与之间函数关系最恰当的是( ) 第4题图 A B C D O P B. t y 0 45 90 D. t y 0 45 90 A. t y 0 45 90 C. t y 0 45 90 5. 在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定( ) A.与轴相离、与轴相切 B.与轴、轴都相离 C.与轴相切、与轴相离 D.与轴、轴都相切 6 如图,若⊙的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为 ( ) A. B. C.2 D. 4 O P Q D B A C 第7题图 R 7.如图,△PQR是⊙O的内接三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是 ( ) A.60 B.65 C.72 D. 75 第6题图 51 第8题图 8.如图,、、、、相互外离,它们的半径都是1,顺次连结五个圆心得到五边形,则图中五个扇形(阴影部分)的面积之和是( ) A. B. C. D. 二 选择题(每题5分,计30分) 9.如图,直角坐标系中一条圆弧经过网格点A、B、C,其中,B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 . A B D C 第10题 第9题图 10. 如图,在ΔABC中,∠A=90°,AB=AC=2cm,⊙A与BC相切于点D,则⊙A的半径长 为 cm. 11.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径弦于),设,,他用含的式子表示图中的弦的长度,通过比较运动的弦和与之垂直的直径的大小关系,发现了一个关于正数的不等式,你也能发现这个不等式吗?写出你发现的不等式 . x y C B D A O (第11题) E (12题图) 12.如图,∠AOB=300,OM=6,那么以M为圆心,4为半径的圆与直OA的位置关系是_________________. 13.如图,△ABC内接于⊙O,∠B=∠OAC,OA=8㎝,则AC的长等于_______㎝。 A B C O (13题图) 14. 阅读下面材料: 51 在数学课上,老师请同学思考如下问题: 请利用直尺和圆规确定图中弧AB所在圆的圆心. A B 小亮的作法如下: 如图, (1) 在弧AB上任意取一点C,分别连接AC,BC; (2) 分别作AC,BC的垂直平分线, 两条垂直平分线交于O点; 所以点O就是所求弧AB的圆心. O A B C 老师说:“小亮的作法正确.” 请你回答:小亮的作图依据是_________________________. 三、解答题(7+7+8+8) A D B O C E 15、已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.求证:(1)△ABC是等边三角形;(2). 16、《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①) 阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径. 再次阅读后,发现AB=______寸,CD=____寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件,并帮助小智求出⊙O的直径. 51 图① 图② 17.如图在⊙O中,AB是直径,CD是弦,AB⊥CD。 (1)P是优弧CAD上一点(不与C、D重合),求证:∠CPD=∠COB; (2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论。 18、如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC 于点E. (1)求证:DE 是⊙O的切线; (2)若△ABC的边长为4,求EF 的长度. 51 参考答案: 1. c 2. D 3. D 4.C 5. A 6.A 7. D 8.B 9. (2,0) 10. 11 、,或,或,或 12.相交;13.; 14.45 15. 证明:(1)连结OD得OD∥AC ∴∠BDO=∠A 又由OB=OD得∠OBD=∠ODB ∴∠OBD=∠A ∴BC=AC 又∵AB=AC ∴△ABC是等边三角形 (2)连结CD,则CD⊥AB ∴D是AB中点 ∵AE=AD=AB ∴EC=3AE ∴. 16. 解:(1)1;10 (2)连接, ∵, ∴. 设,则, 在Rt中,, ∴.∴. 解得,∴⊙的直径为26寸. 17、(1)证明:连接OD,∵AB是直径,AB⊥CD,∴∠COB=∠DOB=。 又∵∠CPD=,∴∠CPD=∠COB。 (2)∠CP′D与∠COB的数量关系是:∠CP′D+∠COB=180°。 证明:∵∠CPD+∠CP′D=180°,∠CPD=∠COB,∴∠CP′D+∠COB=180°。 18、(1)证明:连接, ∵是等边三角形, ∴. ∵, ∴.∵, ∴. ∴. ∴. ∴于点. ∵点在⊙上, ∴是⊙的切线. (2)连接,, ∵为⊙直径, ∴. ∴,. ∵是等边三角形, ∴,.∵, 51 ∴.∴. 九年级数学上册第二十四章圆单元测试卷2 一、选择题(共10小题,每小题3分,共30分) 1.下列说法正确的是( ) A.三点确定一个圆 B.一个三角形只有一个外接圆 C.和半径垂直的直线是圆的切线 D.三角形的内心到三角形三个顶点距离相等 2.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( ) A.42° B.28° C.21° D.20° 3.已知如图,AB是⊙O的直径,弦CD⊥AB于E,CD=6,AE=1,则⊙O的直径为( ) A.6 B.8 C.10 D.12 4.如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( ) A.等于24 B.最小为24 C.等于48 D.最大为48 5.如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( ) 51 A.3 B.2.5 C.4 D.3.5 6.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,则水的最大深度CD为( ) A.4cm B.3cm C.2cm D.1cm 7.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( ) A.甲先到B点 B.乙先到B点 C.甲、乙同时到B D.无法确定 8.在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为( ) A.40cm B.60cm C.80cm D.100cm 9.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( ) A.5πcm B.6πcm C.9πcm D.8πcm 51 10.如图,AB是⊙O的弦,点C在圆上,已知∠OBA=40°,则∠C=( ) A.40° B.50° C.60° D.80° 二、填空题(共6小题,每小题3分,共18分) 11.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD= . 12.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 . 13.如图,已知∠BOA=30°,M为OB边上一点,以M为圆心、2cm为半径作⊙M.点M在射线OB上运动,当OM=5cm时,⊙M与直线OA的位置关系是 . 14.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 . 15.已知扇形的半径为6cm,圆心角的度数为120°,则此扇形的弧长为 cm. 16.如图,半圆O的直径AB=2,弦CD∥AB,∠COD=90°,则图中阴影部分的面积为 . 51 三、解答题(共8题,共72分) 17.圆锥底面圆的半径为3m,其侧面展开图是半圆,求圆锥母线长. 18.在一个底面直径为5cm,高为18cm的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中,能否完全装下?若未能装满,求杯内水面离杯口的距离. 19.如图,AB和CD分别是⊙O上的两条弦,过点O分别作ON⊥CD于点N,OM⊥AB于点M,若ON=AB,证明:OM=CD. 20.如图为桥洞的形状,其正视图是由和矩形ABCD构成.O点为所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求所在⊙O的半径DO. 21.△ABC是⊙O的内接三角形,BC=.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由. 22.如图直角坐标系中,已知A(﹣8,0),B(0,6),点M在线段AB上. 51 (1)如图1,如果点M是线段AB的中点,且⊙M的半径为4,试判断直线OB与⊙M的位置关系,并说明理由; (2)如图2,⊙M与x轴、y轴都相切,切点分别是点E、F,试求出点M的坐标. 23.已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD, (1)求证:DF与⊙O的位置关系并证明; (2)求FG的长. 24.如图,等边△ABC的边长为2,E是边BC上的动点,EF∥AC交边AB于点F,在边AC上取一点P,使PE=EB,连接FP. (1)请直接写出图中与线段EF相等的两条线段;(不再另外添加辅助线) (2)探究:当点E在什么位置时,四边形EFPC是平行四边形?并判断四边形EFPC是什么特殊的平行四边形,请说明理由; (3)在(2)的条件下,以点E为圆心,r为半径作圆,根据⊙E与平行四边形EFPC四条边交点的总个数,求相应的r的取值范围. 51 51 《第24章 圆》 参考答案与试题解析 一、选择题(共10小题,每小题3分,共30分) 1.下列说法正确的是( ) A.三点确定一个圆 B.一个三角形只有一个外接圆 C.和半径垂直的直线是圆的切线 D.三角形的内心到三角形三个顶点距离相等 【考点】圆的认识. 【分析】根据确定圆的条件对A、B进行判断;根据切线的判定定理对C进行判断;根据三角形内心的性质对D进行判断. 【解答】解:A、不共线的三点确定一个圆,所以A选项错误; B、一个三角形只有一个外接圆,所以B选项正确; C、过半径的外端与半径垂直的直线是圆的切线,所以C选项错误; D、三角形的内心到三角形三边的距离相等,所以D选项错误. 故选B. 【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了确定圆的条件和切线的判定. 2.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( ) A.42° B.28° C.21° D.20° 【考点】圆的认识;等腰三角形的性质. 【专题】计算题. 51 【分析】利用半径相等得到DO=DE,则∠E=∠DOE,根据三角形外角性质得∠1=∠DOE+∠E,所以∠1=2∠E,同理得到∠AOC=∠C+∠E=3∠E,然后利用∠E=∠AOC进行计算即可. 【解答】解:连结OD,如图, ∵OB=DE,OB=OD, ∴DO=DE, ∴∠E=∠DOE, ∵∠1=∠DOE+∠E, ∴∠1=2∠E, 而OC=OD, ∴∠C=∠1, ∴∠C=2∠E, ∴∠AOC=∠C+∠E=3∠E, ∴∠E=∠AOC=×84°=28°. 故选B. 【点评】本题考查了圆的认识:掌握与圆有关的概念( 弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质. 3.已知如图,AB是⊙O的直径,弦CD⊥AB于E,CD=6,AE=1,则⊙O的直径为( ) A.6 B.8 C.10 D.12 【考点】垂径定理;勾股定理. 【分析】连接OC,根据题意OE=OC﹣1,CE=3,结合勾股定理,可求出OC的长度,即可求出直径的长度. 【解答】解:连接OC, 51 ∵弦CD⊥AB于E,CD=6,AE=1, ∴OE=OC﹣1,CE=3, ∴OC2=(OC﹣1)2+32, ∴OC=5, ∴AB=10. 故选C. 【点评】本题主要考查了垂径定理、勾股定理,解题的关键在于连接OC,构建直角三角形,根据勾股定理求半径OC的长度. 4.如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( ) A.等于24 B.最小为24 C.等于48 D.最大为48 【考点】垂径定理;勾股定理;梯形中位线定理. 【分析】过圆心O作OE⊥CD于点E,则OE平分CD,在直角△ODE中利用勾股定理即可求得OE的长,即梯形DMNC的中位线,根据梯形的面积等于OE•CD即可求得. 【解答】解:过圆心O作OE⊥CD于点E, 连接OD.则DE=CD=×6=3. 在直角△ODE中,OD=AB=×10=5, OE===4. 则S四边形DMNC=OE•CD=4×6=24. 故选A. 51 【点评】本题考查了梯形的中位线以及垂径定理,正确作出辅助线是关键. 5.如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( ) A.3 B.2.5 C.4 D.3.5 【考点】垂径定理;勾股定理. 【分析】连接OA,根据垂径定理得到AP=AB,利用勾股定理得到答案. 【解答】解:连接OA, ∵AB⊥OP, ∴AP==3,∠APO=90°,又OA=5, ∴OP===4, 故选C. 【点评】本题考查的是垂径定理的应用,掌握垂直于弦的直径平分这条弦是解题的关键. 6.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,则水的最大深度CD为( ) A.4cm B.3cm C.2cm D.1cm 51 【考点】垂径定理的应用;勾股定理. 【分析】根据题意可得出AO=5cm,AC=4cm,进而得出CO的长,即可得出答案. 【解答】解:如图所示:∵输水管的半径为5cm,水面宽AB为8cm,水的最大深度为CD, ∴DO⊥AB, ∴AO=5cm,AC=4cm, ∴CO==3(cm), ∴水的最大深度CD为:2cm. 故选:C. 【点评】本题考查的是垂径定理的应用及勾股定理,根据构造出直角三角形是解答此题的关键. 7.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( ) A.甲先到B点 B.乙先到B点 C.甲、乙同时到B D.无法确定 【考点】圆的认识. 【专题】应用题. 【分析】甲虫走的路线应该是4段半圆的弧长,那么应该是π(AA1+A1A2+A2A3+A3B)=π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,因此两个同时到B点. 【解答】解:π(AA1+A1A2+A2A3+A3B)=π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等, 因此两个同时到B点. 故选C. 【点评】本题考查了圆的认识,主要掌握弧长的计算公式. 8.在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为( ) 51 A.40cm B.60cm C.80cm D.100cm 【考点】垂径定理的应用;勾股定理. 【分析】连接OA,过点O作OE⊥AB,交AB于点M,由垂径定理求出AM的长,再根据勾股定理求出OM的长,进而可得出ME的长. 【解答】解:连接OA,过点O作OE⊥AB,交AB于点M, ∵直径为200cm,AB=160cm, ∴OA=OE=100cm,AM=80cm, ∴OM===60cm, ∴ME=OE﹣OM=100﹣60=40cm. 故选:A. 【点评】本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键. 9.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( ) A.5πcm B.6πcm C.9πcm D.8πcm 【考点】圆心角、弧、弦的关系;等边三角形的判定与性质. 【分析】如图,连接OD、OC.根据圆心角、弧、弦的关系证得△AOD是等边三角形,则⊙O的半径长为BC=4cm;然后由圆的周长公式进行计算. 【解答】解:如图,连接OD、OC. ∵AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm, 51 ∴==, ∴∠AOD=∠DOC=∠BOC=60°. 又OA=OD, ∴△AOD是等边三角形, ∴OA=AD=4cm, ∴⊙O的周长=2×4π=8π(cm). 故选:D. 【点评】本题考查了圆心角、弧、弦的关系,等边三角形的判定.该题利用“有一内角是60度的等腰三角形为等边三角形”证得△AOD是等边三角形. 10.如图,AB是⊙O的弦,点C在圆上,已知∠OBA=40°,则∠C=( ) A.40° B.50° C.60° D.80° 【考点】圆周角定理. 【分析】首先根据等边对等角即可求得∠OAB的度数,然后根据三角形的内角和定理求得∠AOB的度数,再根据圆周角定理即可求解. 【解答】解:∵OA=OB, ∴∠OAB=∠OBA=40°, ∴∠AOB=180°﹣40°﹣40°=100°. ∴∠C=∠AOB=×100°=50°. 故选B. 【点评】本题考查了等腰三角形的性质定理以及圆周角定理,正确理解定理是关键. 二、填空题(共6小题,每小题3分,共18分) 51 11.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD= 80° . 【考点】圆周角定理;平行线的性质. 【分析】根据平行线的性质由AB∥CD得到∠C=∠ABC=40°,然后根据圆周角定理求解. 【解答】解:∵AB∥CD, ∴∠C=∠ABC=40°, ∴∠BOD=2∠C=80°. 故答案为80°. 【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.也考查了平行线的性质. 12.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 3<r<5 . 【考点】点与圆的位置关系. 【分析】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内. 【解答】解:在直角△ABD中,CD=AB=4,AD=3, 则BD==5. 由图可知3<r<5. 故答案为:3<r<5. 【点评】此题主要考查了点与圆的位置关系,解决本题要注意点与圆的位置关系,要熟悉勾股定理,及点与圆的位置关系. 13.如图,已知∠BOA=30°,M为OB边上一点,以M为圆心、2cm为半径作⊙M.点M在射线OB上运动,当OM=5cm时,⊙M与直线OA的位置关系是 相离 . 51 【考点】直线与圆的位置关系. 【专题】常规题型. 【分析】作MH⊥OA于H,如图,根据含30度的直角三角形三边的关系得到MH=OM=,则MH大于⊙M的半径,然后根据直线与圆的位置关系的判定方法求解. 【解答】解:作MH⊥OA于H,如图, 在Rt△OMH中,∵∠HOM=30°, ∴MH=OM=, ∵⊙M的半径为2, ∴MH>2, ∴⊙M与直线OA的位置关系是相离. 故答案为相离. 【点评】本题考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,直线l和⊙O相交⇔d<r;直线l和⊙O相切⇔d=r;直线l和⊙O相离⇔d>r. 14.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 2 . 【考点】正多边形和圆. 【分析】连接AC、OE、OF,作OM⊥EF于M,先求出圆的半径,在RT△OEM中利用30度角的性质即可解决问题. 【解答】解;连接AC、OE、OF,作OM⊥EF于M, ∵四边形ABCD是正方形, ∴AB=BC=4,∠ABC=90°, 51 ∴AC是直径,AC=4, ∴OE=OF=2,∵OM⊥EF, ∴EM=MF, ∵△EFG是等边三角形, ∴∠GEF=60°, 在RT△OME中,∵OE=2,∠OEM=∠GEF=30°, ∴OM=,EM=OM=, ∴EF=2. 故答案为2. 【点评】本题考查正多边形与圆、等腰直角三角形的性质、等边三角形的性质等知识,解题的关键是熟练应用这些知识解决问题,属于中考常考题型. 15.已知扇形的半径为6cm,圆心角的度数为120°,则此扇形的弧长为 4π cm. 【考点】弧长的计算. 【分析】在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=nπR÷180. 【解答】解:∵扇形的半径为6cm,圆心角的度数为120°, ∴扇形的弧长为: =4πcm; 故答案为:4π. 【点评】本题考查了弧长的计算.解答该题需熟记弧长的公式l=. 16.如图,半圆O的直径AB=2,弦CD∥AB,∠COD=90°,则图中阴影部分的面积为 . 51 【考点】扇形面积的计算. 【分析】由CD∥AB可知,点A、O到直线CD的距离相等,结合同底等高的三角形面积相等即可得出S△ACD=S△OCD,进而得出S阴影=S扇形COD,根据扇形的面积公式即可得出结论. 【解答】解:∵弦CD∥AB, ∴S△ACD=S△OCD, ∴S阴影=S扇形COD=•π•=×π×=. 故答案为:. 【点评】本题考查了扇形面积的计算以及平行线的性质,解题的关键是找出S阴影=S扇形COD.本题属于基础题,难度不大,解决该题型题目时,通过分割图形找出面积之间的关系是关键. 三、解答题(共8题,共72分) 17.圆锥底面圆的半径为3m,其侧面展开图是半圆,求圆锥母线长. 【考点】圆锥的计算. 【分析】侧面展开后得到一个半圆就是底面圆的周长.依此列出方程即可. 【解答】解:设母线长为x,根据题意得 2πx÷2=2π×3, 解得x=6. 故圆锥的母线长为6m. 【点评】本题考查圆锥的母线长的求法,注意利用圆锥的弧长等于底面周长这个知识点. 18.在一个底面直径为5cm,高为18cm的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中,能否完全装下?若未能装满,求杯内水面离杯口的距离. 【考点】圆柱的计算. 【专题】计算题. 【分析】设将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中时,水面高为xcm,根据水的体积不变和圆柱的条件公式得到π•()2•x=π•()2•18,解得x=12.5,然后把12.5与10进行大小比较即可判断能否完全装下. 【解答】解:设将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中时,水面高为xcm, 根据题意得π•()2•x=π•()2•18, 51 解得x=12.5, ∵12.5>10, ∴不能完全装下. 【点评】本题考查了圆柱:圆柱的母线(高)等于展开后所得矩形的宽,圆柱的底面周长等于矩形的长;圆柱的侧面积=底面圆的周长×高;圆柱的表面积=上下底面面积+侧面积;圆柱的体积=底面积×高. 19.如图,AB和CD分别是⊙O上的两条弦,过点O分别作ON⊥CD于点N,OM⊥AB于点M,若ON=AB,证明:OM=CD. 【考点】垂径定理;全等三角形的判定与性质. 【专题】证明题. 【分析】设圆的半径是r,ON=x,则AB=2x,在直角△CON中利用勾股定理即可求得CN的长,然后根据垂径定理求得CD的长,然后在直角△OAM中,利用勾股定理求得OM的长,即可证得. 【解答】证明:设圆的半径是r,ON=x,则AB=2x, 在直角△CON中,CN==, ∵ON⊥CD, ∴CD=2CN=2, ∵OM⊥AB, ∴AM=AB=x, 在△AOM中,OM==, ∴OM=CD. 51 【点评】此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解. 20.如图为桥洞的形状,其正视图是由和矩形ABCD构成.O点为所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求所在⊙O的半径DO. 【考点】垂径定理的应用;矩形的性质. 【分析】先根据垂径定理求出DF的长,再由勾股定理即可得出结论. 【解答】解:∵OE⊥弦CD于点F,CD为8米,EF为2米, ∴EO垂直平分CD,DF=4m,FO=DO﹣2, 在Rt△DFO中,DO2=FO2+DF2,则DO2=(DO﹣2)2+42,解得:DO=5; 答:所在⊙O的半径DO为5m. 【点评】本题考查的是垂径定理的应用,此类题中一般使用列方程的方法,这种用代数方法解决几何问题即几何代数解的数学思想方法一定要掌握. 21.△ABC是⊙O的内接三角形,BC=.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由. 51 【考点】直线与圆的位置关系. 【分析】作OF⊥l于F,CE⊥l于E,设AD=a,则AB=2AD=2a,只要证明OF是梯形ADEC的中位线即可解决问题. 【解答】解:图形如图所示,直线l与⊙O相切. 理由:作OF⊥l于F,CE⊥l于E, ∵AC是直径, ∴∠ABC=90°, ∵l⊥BD, ∴∠BDE=90°, ∵OF⊥l,CE⊥l, ∴AD∥OF∥CE, ∵AO=OC, ∴DF=FE, ∴OF=(AD+CE), 设AD=a,则AB=2AD=2a, ∵∠ABC=∠BDE=∠CED=90°, ∴四边形BDEC是矩形, ∴CE=BD=3a, ∴OF=2a, ∵在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2a, ∴AC=4a, ∴OF=OA=2a, ∴直线l是⊙O切线. 51 【点评】本题考查直线与圆的位置关系、图形中位线的性质等知识,解题的关键是添加辅助线,要证明切线的方法有两种,一是连半径,证垂直,二是作垂直,正半径,此题则是运用第二种方法. 22.如图直角坐标系中,已知A(﹣8,0),B(0,6),点M在线段AB上. (1)如图1,如果点M是线段AB的中点,且⊙M的半径为4,试判断直线OB与⊙M的位置关系,并说明理由; (2)如图2,⊙M与x轴、y轴都相切,切点分别是点E、F,试求出点M的坐标. 【考点】直线与圆的位置关系;坐标与图形性质. 【分析】(1)设线段OB的中点为D,连结MD,根据三角形的中位线求出MD,根据直线和圆的位置关系得出即可; (2)求出过点A、B的一次函数关系式是y=x+6,设M(a,﹣a),把x=a,y=﹣a代入y=x+6得出关于a的方程,求出即可. 【解答】解:(1)直线OB与⊙M相切, 理由:设线段OB的中点为D,连结MD,如图1, 51 ∵点M是线段AB的中点,所以MD∥AO,MD=4. ∴∠AOB=∠MDB=90°, ∴MD⊥OB,点D在⊙M上, 又∵点D在直线OB上, ∴直线OB与⊙M相切; , (2)解:连接ME,MF,如图2, ∵A(﹣8,0),B(0,6), ∴设直线AB的解析式是y=kx+b, ∴, 解得:k=,b=6, 即直线AB的函数关系式是y=x+6, ∵⊙M与x轴、y轴都相切, ∴点M到x轴、y轴的距离都相等,即ME=MF, 设M(a,﹣a)(﹣8<a<0), 把x=a,y=﹣a代入y=x+6, 得﹣a=a+6,得a=﹣, ∴点M的坐标为(﹣,). 【点评】本题考查了直线和圆的位置关系,用待定系数法求一次函数的解析式的应用,能综合运用知识点进行推理和计算是解此题的关键,注意:直线和圆有三种位置关系:已知⊙O的半径为r,圆心O到直线l的距离是,当d=r时,直线l和⊙O相切. 51 23.已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD, (1)求证:DF与⊙O的位置关系并证明; (2)求FG的长. 【考点】直线与圆的位置关系;等边三角形的性质;勾股定理;垂径定理. 【分析】(1)连接OD,证∠ODF=90°即可. (2)利用△ADF是30°的直角三角形可求得AF长,同理可利用△FHC中的60°的三角函数值可求得FG长. 【解答】(1)证明:连接OD, ∵以等边三角形ABC的边AB为直径的半圆与BC边交于点D, ∴∠B=∠C=∠ODB=60°, ∴OD∥AC, ∵DF⊥AC, ∴∠CFD=∠ODF=90°,即OD⊥DF, ∵OD是以边AB为直径的半圆的半径, ∴DF是圆O的切线; (2)∵OB=OD=AB=6,且∠B=60°, ∴BD=OB=OD=6, ∴CD=BC﹣BD=AB﹣BD=12﹣6=6, ∵在Rt△CFD中,∠C=60°, ∴∠CDF=30°, ∴CF=CD=×6=3, ∴AF=AC﹣CF=12﹣3=9, ∵FG⊥AB, ∴∠FGA=90°, 51 ∵∠FAG=60°, ∴FG=AFsin60°=. 【点评】本题主要考查了直线与圆的位置关系、等边三角形的性质、垂径定理等知识,判断直线和圆的位置关系,一般要猜想是相切,那么证直线和半径的夹角为90°即可;注意利用特殊的三角形和三角函数来求得相应的线段长. 24.如图,等边△ABC的边长为2,E是边BC上的动点,EF∥AC交边AB于点F,在边AC上取一点P,使PE=EB,连接FP. (1)请直接写出图中与线段EF相等的两条线段;(不再另外添加辅助线) (2)探究:当点E在什么位置时,四边形EFPC是平行四边形?并判断四边形EFPC是什么特殊的平行四边形,请说明理由; (3)在(2)的条件下,以点E为圆心,r为半径作圆,根据⊙E与平行四边形EFPC四条边交点的总个数,求相应的r的取值范围. 【考点】点与圆的位置关系;等边三角形的性质;平行四边形的判定;菱形的判定. 【专题】探究型. 【分析】(1)由平行易得△BFE是等边三角形,那么各边是相等的; (2)当点E是BC的中点时,△PEC为等边三角形,可得到PC=EC=BE=EF,也就得到了四边形EFPC是平行四边形,再有EF=EC可证为菱形; (3)根据各点到圆心的距离作答即可. 【解答】解:(1)如图,∵△ABC是等边三角形, ∴∠B=∠A=∠C=60°. 51 又∵EF∥AC, ∴∠BFE=∠A=60°,∠BEF=∠C=60°, ∴△BFE是等边三角形,PE=EB, ∴EF=BE=PE=BF; (2)当点E是BC的中点时,四边形是菱形; ∵E是BC的中点, ∴EC=BE, ∵PE=BE, ∴PE=EC, ∵∠C=60°, ∴△PEC是等边三角形, ∴PC=EC=PE, ∵EF=BE, ∴EF=PC, 又∵EF∥CP, ∴四边形EFPC是平行四边形, ∵EC=PC=EF, ∴平行四边形EFPC是菱形; (3)如图所示: 当点E是BC的中点时,EC=1,则NE=ECcos30°=, 当0<r<时,有两个交点; 当r=时,有四个交点; 当<r<1时,有六个交点; 当r=1时,有三个交点; 当r>1时,有0个交点. 51 【点评】本题综合考查了等边三角形的性质和判定,菱形的判定及点和圆的位置关系等知识点.注意圆和线段有交点,应根据半径作答. 九年级数学上册第二十四章圆单元测试卷3 一、填空题 1.已知点O为△ABC的外心,若∠A=80°,则∠BOC的度数为( ) A.40° B.80° C.160° D.120° 2.点P在⊙O内,OP=2cm,若⊙O的半径是3cm,则过点P的最短弦的长度为( ) A.1cm B.2cm C. cm D. cm 3.已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,,那么点P与⊙O的位置关系是( ) A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定 4.如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( ) 51 A. B. C. D. 5.在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定( ) A.与x轴相离,与y轴相切 B.与x轴,y轴都相离 C.与x轴相切,与y轴相离 D.与x轴,y轴都相切 6.如图,⊙O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,若⊙O的半径为2,则CD的长为( ) A.2 B.4 C.2 D.4 7.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是( ) A.60 B.65 C.72 D.75 8.如图,⊙A,⊙B,⊙C,⊙D,⊙E互相外离,它们的半径都是1,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积是( ) 51 A.π B.1.5π C.2π D.2.5π 二、选择题 9.如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 . 10.如图,在△ABC中,∠A=90°,AB=AC=2cm,⊙A与BC相切于点D,则⊙A的半径长为 cm. 11.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形性质描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于点E,设AE=x,BE=y,用含x,y的式子表示图中的弦CD的长度),通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式. 12.如图,∠AOB=30°,OM=6,那么以M为圆心,4为半径的圆与直OA的位置关系是 . 13.如图,△ABC内接于⊙O,∠B=∠OAC,OA=8cm,则AC= cm. 51 14.阅读下面材料: 在数学课上,老师请同学思考如下问题: 小亮的作法如下: 老师说:“小亮的作法正确.” 请你回答:小亮的作图依据是 . 三、解答题(7+7+8+8) 15.已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E. 求证:(1)△ABC是等边三角形; (2). 51 16.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①) 阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径. 再次阅读后,发现AB= 寸,CD= 寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件,并帮助小智求出⊙O的直径. 17.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD. (1)P是上一点(不与C、D重合),求证:∠CPD=∠COB; (2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论. 51 18.如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E. (1)求证:DE是⊙O的切线; (2)若△ABC的边长为4,求EF的长度. 51 《第24章 圆》(北京市西城区重点中学) 参考答案与试题解析 一、填空题 1.已知点O为△ABC的外心,若∠A=80°,则∠BOC的度数为( ) A.40° B.80° C.160° D.120° 【考点】三角形的外接圆与外心. 【分析】根据圆周角定理得∠BOC=2∠A=160°. 【解答】解:∵点O为△ABC的外心,∠A=80°, ∴∠BOC=2∠A=160°. 故选C. 【点评】熟练运用圆周角定理计算,即在同圆或等圆中同弧所对的圆周角等于它所对的圆心角的一半. 2.点P在⊙O内,OP=2cm,若⊙O的半径是3cm,则过点P的最短弦的长度为( ) A.1cm B.2cm C. cm D. cm 【考点】垂径定理;勾股定理. 【专题】计算题. 【分析】过P作AB⊥OP交圆与A、B两点,连接OA,故AB为最短弦长,再解Rt△OPA,即可求得AB的长度,即过点P的最短弦的长度. 【解答】解:过P作AB⊥OP交圆与A、B两点,连接OA,如下图所示: 故AB为最短弦长, 由垂径定理可得:AP=PB 已知OA=3,OP=2 在Rt△OPA中,由勾股定理可得: AP2=OA2﹣OP2 ∴AP==cm ∴AB=2AP=2cm 故此题选D. 51 【点评】本题考查了最短弦长的判定以及垂径定理的运用. 3.已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,,那么点P与⊙O的位置关系是( ) A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定 【考点】点与圆的位置关系. 【分析】根据题意可知点P可能在圆外也可能在圆上,也可能在圆内,所以无法确定. 【解答】解:∵PA=,⊙O的直径为2 ∴点P的位置有三种情况:①在圆外,②在圆上,③在圆内. 故选D. 【点评】本题考查了圆的认识,做题时注意多种情况的考虑. 4.如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( ) A. B. C. D. 【考点】动点问题的函数图象. 【分析】根据题意,分P在OC、CD、DO之间3个阶段,分别分析变化的趋势,又由点P作匀速运动,故①③都是线段,分析选项可得答案. 51 【解答】解:根据题意,分3个阶段; ①P在OC之间,∠APB逐渐减小,到C点时,为45°, ②P在CD之间,∠APB保持45°,大小不变, ③P在DO之间,∠APB逐渐增大,到O点时,为90°; 又由点P作匀速运动,故①③都是线段; 分析可得:B符合3个阶段的描述; 故选:B. 【点评】本题主要考查了函数图象与几何变换,解决此类问题,注意将过程分成几个阶段,依次分析各个阶段得变化情况,进而综合可得整体得变化情况. 5.在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定( ) A.与x轴相离,与y轴相切 B.与x轴,y轴都相离 C.与x轴相切,与y轴相离 D.与x轴,y轴都相切 【考点】直线与圆的位置关系;坐标与图形性质. 【分析】本题应将该点的横纵坐标分别与半径对比,大于半径的相离,等于半径的相切. 【解答】解:∵是以点(2,3)为圆心,2为半径的圆, 如图所示: ∴这个圆与y轴相切,与x轴相离. 故选A. 【点评】直线与圆相切,直线到圆的距离等于半径;与圆相离,直线到圆的距离大于半径. 6.如图,⊙O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,若⊙O的半径为2,则CD的长为( ) 51 A.2 B.4 C.2 D.4 【考点】切线的性质. 【专题】压轴题. 【分析】连接OC,BC,AB是直径,CD是切线,先求得∠OCD=90°再求∠COB=2∠A=60°,利用三角函数即可求得CD的值. 【解答】解:连接OC,BC,AB是直径,则∠ACB=90°, ∵CD是切线, ∴∠OCD=90°, ∵∠A=30°, ∴∠COB=2∠A=60°,CD=OC•tan∠COD=2. 故选A. 【点评】本题利用了切线的性质,直径对的圆周角是直角求解. 7.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是( ) A.60 B.65 C.72 D.75 【考点】三角形的外接圆与外心;等边三角形的性质;正方形的性质. 【分析】根据等边三角形和正方形的性质,求得中心角∠POR和∠POD,二者的差就是所求. 【解答】解:连结OD,如图, 51 ∵△PQR是⊙O的内接正三角形, ∴PQ=PR=QR, ∴∠POR=×360°=120°, ∵四边形ABCD是⊙O的内接正方形, ∴∠AOD=90°, ∴∠DOP=×90°=45°, ∴∠AOQ=∠POR﹣∠DOP=75°. 故选D. 【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理. 8.如图,⊙A,⊙B,⊙C,⊙D,⊙E互相外离,它们的半径都是1,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积是( ) A.π B.1.5π C.2π D.2.5π 【考点】扇形面积的计算;多边形内角与外角. 【专题】压轴题. 【分析】圆心角之和等于五边形的内角和,由于半径相同,那么根据扇形的面积2公式计算即可. 【解答】解:图中五个扇形(阴影部分)的面积是=1.5π 故选B. 【点评】解决本题的关键是把阴影部分当成一个扇形的面积来求,圆心角为五边形的内角和. 51 二、选择题 9.如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 (2,0) . 【考点】确定圆的条件;坐标与图形性质. 【专题】网格型. 【分析】根据垂径定理的推论:弦的垂直平分线必过圆心,可以作弦AB和BC的垂直平分线,交点即为圆心. 【解答】解:根据垂径定理的推论:弦的垂直平分线必过圆心, 可以作弦AB和BC的垂直平分线,交点即为圆心. 如图所示,则圆心是(2,0). 故答案为:(2,0) 【点评】能够根据垂径定理的推论得到圆心的位置. 10.如图,在△ABC中,∠A=90°,AB=AC=2cm,⊙A与BC相切于点D,则⊙A的半径长为 cm. 【考点】切线的性质. 【专题】压轴题. 51 【分析】连接AD,则有AD是△ABC的斜边上的高,可判定△ABC是等腰直角三角形,所以BC=AB=2,利用点D是斜边的中点,可求AD=BC=cm. 【解答】解:连接AD; ∵∠A=90°,AB=AC=2cm, ∴△ABC是等腰直角三角形, ∴BC=AB=2; ∵点D是斜边的中点, ∴AD=BC=cm. 【点评】本题利用了切线的性质,等腰直角三角形的判定和性质求解. 11.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形性质描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于点E,设AE=x,BE=y,用含x,y的式子表示图中的弦CD的长度),通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式. 【考点】垂径定理的应用. 【专题】数形结合. 【分析】此题中隐含的不等关系:直径是圆中最长的弦,所以AB≥CD. 首先可以表示出AB=x+y,再根据相交弦定理的推论和垂径定理,得CD=2CE=2. 【解答】解:∵直径AB⊥弦CD于点E, ∴CE=DE, 根据相交弦定理的推论,得CE2=AE•BE,则CE=, 51 ∴CD=2CE=2. 又∵AB=x+y,且AB≥CD, ∴x+y≥2. 【点评】本题考查:直径是圆中最长的弦;相交弦定理的推论以及垂径定理的综合应用. 12.如图,∠AOB=30°,OM=6,那么以M为圆心,4为半径的圆与直OA的位置关系是 相交 . 【考点】直线与圆的位置关系. 【分析】利用直线l和⊙O相切⇔d=r,进而判断得出即可. 【解答】解:过点M作MD⊥AO于点D, ∵∠AOB=30°,OM=6, ∴MD=3, ∴MD<r ∴以点m为圆心,半径为34的圆与OA的位置关系是:相交. 故答案为:相交. 【点评】此题主要考查了直线与圆的位置,正确掌握直线与圆相切时d与r的关系是解题关键. 13.如图,△ABC内接于⊙O,∠B=∠OAC,OA=8cm,则AC= 8 cm. 【考点】圆周角定理. 【专题】压轴题. 【分析】结合等腰三角形的性质、圆周角定理、三角形的内角和定理求得三角形AOC是等腰直角三角形,再根据勾股定理即可求解. 51 【解答】解:连接OC. ∵OA=OC, ∴∠OAC=∠OCA. 又∵∠B=∠OAC=∠AOC, ∴∠AOC=90°. ∴AC=OA=8cm. 【点评】此题综合运用了等腰三角形的性质、圆周角定理、三角形的内角和定理以及勾股定理. 14.阅读下面材料: 在数学课上,老师请同学思考如下问题: 小亮的作法如下: 老师说:“小亮的作法正确.” 请你回答:小亮的作图依据是 垂径定理 . 51 【考点】垂径定理的应用;作图—复杂作图. 【分析】利用垂径定理得出任意两弦的垂直平分线交点即可. 【解答】解:根据小亮作图的过程得到:小亮的作图依据是垂径定理. 故答案是:垂径定理. 【点评】此题主要考查了复杂作图以及垂径定理,熟练利用垂径定理的性质是解题关键. 三、解答题(7+7+8+8) 15.已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E. 求证:(1)△ABC是等边三角形; (2). 【考点】等边三角形的判定;圆周角定理. 【专题】证明题. 【分析】(1)连接OD,根据切线的性质得到OD⊥DE,从而得到平行线,得到∠ODB=∠A,∠ODB=∠B,则∠A=∠B,得到AC=BC,从而证明该三角形是等边三角形; (2)再根据在圆内直径所对的角是直角这一性质,推出30°的直角三角形,根据30°所对的直角边是斜边的一半即可证明. 【解答】证明:(1)连接OD,得OD∥AC; ∴∠BDO=∠A; 又OB=OD, ∴∠OBD=∠ODB; ∴∠OBD=∠A; ∴BC=AC; 又∵AB=AC, ∴△ABC是等边三角形; 51 (2)如上图,连接CD,则CD⊥AB; ∴D是AB中点; ∵AE=AD=AB, ∴EC=3AE; ∴AE=CE. 【点评】本题中作好辅助线是解题的关键,连接过切点的半径是圆中常见的辅助线作法之一.另外还要掌握等边三角形的判定和性质以及30°的直角三角形的性质. 16.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①) 阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径. 51 再次阅读后,发现AB= 1 寸,CD= 10 寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件,并帮助小智求出⊙O的直径. 【考点】垂径定理的应用;勾股定理. 【分析】根据题意容易得出AB和CD的长;连接OB,设半径CO=OB=x寸,先根据垂径定理求出CA的长,再根据勾股定理求出x的值,即可得出直径. 【解答】解:根据题意得:AB=1寸,CD=10寸; 故答案为:1,10; (2)连接CO,如图所示: ∵BO⊥CD, ∴. 设CO=OB=x寸,则AO=(x﹣1)寸, 在Rt△CAO中,∠CAO=90°, ∴AO2+CA2=CO2. ∴(x﹣1)2+52=x2. 解得:x=13, ∴⊙O的直径为26寸. 【点评】本题考查了勾股定理在实际生活中的应用;根据题意作出辅助线,构造出直角三角形,运用勾股定理得出方程是解答此题的关键. 17.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD. (1)P是上一点(不与C、D重合),求证:∠CPD=∠COB; (2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论. 51 【考点】圆心角、弧、弦的关系. 【专题】几何综合题. 【分析】(1)根据垂径定理知,弧CD=2弧BC,由圆周角定理知,弧BC的度数等于∠BOC的度数,弧AD的度数等于∠CPD的2倍, 可得:∠CPD=∠COB; (2)根据圆内接四边形的对角互补知,∠CP′D=180°﹣∠CPD,而:∠CPD=∠COB,∴∠CP′D+∠COB=180°. 【解答】(1)证明:连接OD, ∵AB是直径,AB⊥CD, ∴. ∴∠COB=∠DOB=∠COD. 又∵∠CPD=∠COD, ∴∠CPD=∠COB. (2)解:∠CP′D+∠COB=180°. 理由如下:连接OD, ∵∠CPD+∠CP′D=180°,∠COB=∠DOB=∠COD, 又∵∠CPD=∠COD, ∴∠COB=∠CPD, ∴∠CP′D+∠COB=180°. 【点评】本题利用了垂径定理和圆周角定理及圆内接四边形的性质求解. 51 18.如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E. (1)求证:DE是⊙O的切线; (2)若△ABC的边长为4,求EF的长度. 【考点】切线的判定;等边三角形的性质. 【分析】(1)连接OD,根据等边三角形的性质求出∠ODE=90°,根据切线的判定定理证明即可; (2)连接AD,BF,根据等边三角形的性质求出DC、CF,根据直角三角形的性质求出EC,结合图形计算即可. 【解答】(1)证明:如图1,连接OD, ∵△ABC是等边三角形, ∴∠B=∠C=60°. ∵OB=OD, ∴∠ODB=∠B=60°. ∵DE⊥AC, ∴∠DEC=90°. ∴∠EDC=30°. ∴∠ODE=90°. ∴DE⊥OD于点D. ∵点D在⊙O上, ∴DE是⊙O的切线; (2)解:如图2,连接AD,BF, ∵AB为⊙O直径, ∴∠AFB=∠ADB=90°. ∴AF⊥BF,AD⊥BD. ∵△ABC是等边三角形, 51 ∴,. ∵∠EDC=30°, ∴. ∴FE=FC﹣EC=1. 【点评】本题考查的是切线的判定、等边三角形的性质以及直角三角形的性质,掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键. 51查看更多