- 2021-11-06 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学总复习专题课件:两圆的公切线3
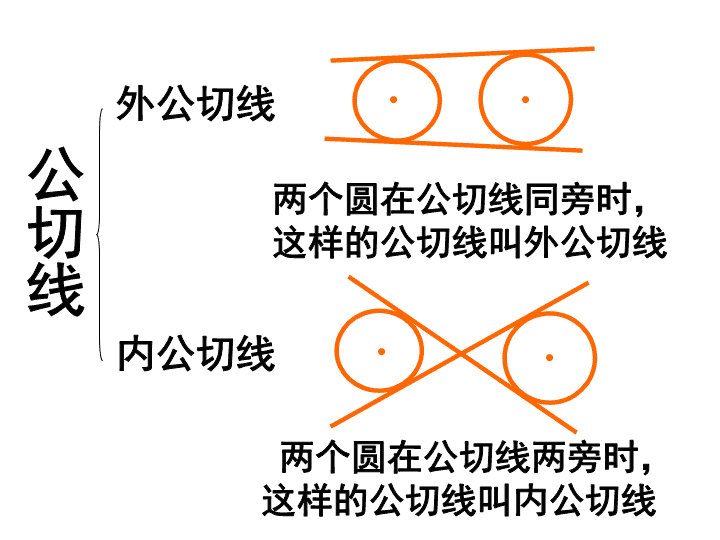
复习(八) 两圆的公切线 B 外公切线 内公切线 两个圆在公切线同旁时,这样的公切线叫 外公切线 两个圆在公切线两旁时,这样的公切线叫 内公切线 公切线 ⑴ ⑵ ⑶ ⑷ ⑸ 4条 3条 2条 1条 无 公切线的条数 1 、连结两圆心与两切点,构造出直角梯形; 2 、过一点做直角梯形的高 , 分成矩形和直角三角形; 3 、把求外公切线长转化为解直角三角形,利用解直角三角形的方法解决问题。 解题思路 外公切线解题基本图形 设两圆的半径分别为 R 和 r ( R ﹥ r ), 圆心距为 d ,则两圆的外公切线长 = ( d ﹥ R-r ) 若两圆连心线与两圆外公切线的夹角为 α ,则 sin α = ( d ﹥ R+r ) 设两圆的半径分别为 R 和 r ( R ﹥ r ), 圆心距为 d , 则 两圆的内公切线长 = 若两圆连心线与两圆内公切线的夹角为 α ,则 sin α = 1 、已知 :⊙ 0 1 ,⊙ 0 2 的半径分别为 2cm 和 3cm , 它们切于点 T 。 外公切线 AB 与⊙ 0 1 、⊙ 0 2 分别切于点 A 、 B ,则外公切线的长 AB= 。 检测练习 2 、已知 :⊙ 0 1 ,⊙ 0 2 外切于点 C ,直线 AB 分别切⊙ 0 1 ,⊙ 0 2 于 A 、 B 两点,⊙ 0 2 的半径为 1 , AB= , 则⊙ 0 1 的半径是 。 2 3. 已知⊙ O 1 的半径 4cm , ⊙ O 2 的半径 1cm , 两圆的圆心距为 6cm , 那么两圆的外公切线长为 cm ,内公切线长为 cm ,连心线与外公切线的夹角为 ,连心线与内公切线夹角的正弦值是 . 30° 4 、已知⊙ O 1 和⊙ O 2 的外切于点 P , AB 切⊙ O 1 于 A , 切⊙ O 2 于 B. ⑴若 连结 PA 、 PB ,求证: PA⊥PB. ⑵若 R 1 =5cm , R 2 =3cm , PQ⊥AB 于 Q ,求 PQ 的长 . Q O 1 O 2 A B P 引伸 . 如图, ⊙ O 1 与⊙ O 2 外切于点 P , AB 是两圆的公切线,切点为 B , A. 连结 BP 并延长交⊙ O 2 于 C ,过 C 作 AB 的平行线交⊙ O 1 于 D , E. ⑴求证: AC 是⊙ O 1 的直径; ⑵试判断线段 BD 、 BA 、 BE 的大小关系,并证明 . A O 1 O 2 B P C D E 5. 如图⊙ O 1 与⊙ O 2 相交于 A , B 两点, AB 的延长线与两圆的公切线 CD 交于点 H , 切点为 C , D , AD 交⊙ O 2 于 F , DB 的延长线交⊙ O 1 于 E , EF 交 AB 于 G. ⑴求证: AD·GB=HD·EB ; A O 1 O 2 B C D H E F G ⑵若 CD=6 , GF=1 , 求 的值 . EB GB 课堂作业 1. 已知两等圆和另一个圆两两互相外切 , 且都与同一条直线相切 , 求等圆与另一个圆的半径之比 . B C A O M N P X Y 2. 圆心A(0,3),⊙A与X轴相切,⊙B的圆心在X轴的正半轴上,且⊙B与⊙A外切于点P,两圆的公切线MP交Y轴于点M,交X轴于N . ( 1 ). 若 sin∠OAB =0.8 ,求直线 MP 的解析式及经过 M,N,B 三点的抛物线的解析式 (2) 若⊙A的位置大小不变,⊙B的圆心在X轴正半轴移动并使⊙A与⊙B始终外切,过M作⊙B的切线MC,切点为C,在此变化过程中探究: ①四边形OMCB 是什么四边形, 对你的结论加以 证明. B C A O M N P X Y查看更多