九年级上册青岛版数学课件3-3圆周角（2）

九年级上册青岛版数学课件3-3圆周角（2）

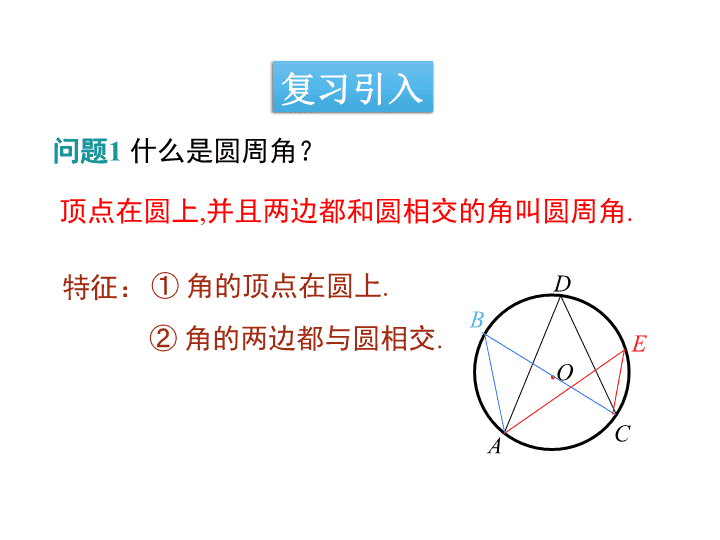
3.3圆周角（2） 学习目标1.了解同弧上圆周角的关系.2.了解直径所对的圆周角的度数. 复习引入问题1什么是圆周角？特征：①角的顶点在圆上.②角的两边都与圆相交.顶点在圆上,并且两边都和圆相交的角叫圆周角.●OBACDE 问题2什么是圆周角定理？圆周角等于它所对弧上的圆心角的一半.●OABC●OABC●OABC即∠ABC=∠AOC. 讲授新课圆周角定理的推论2同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等. 如图,在☉O中,D是的中点,BD,AC相交于点E.求证:△ABD∽△EBC.证明:∵D是的中点,∴=.∴∠ABD=∠DBC.又∵∠ADB与∠ACB是所对的圆周角,∴∠ADB=∠ACB.∴△ABD∽△EBC. 直径所对应的圆周角思考：如图，AC是圆O的直径，则∠ADC=，∠ABC=.90°90°推论：直径所对的圆周角是直角.反之，90°的圆周角所对的弦是直径. 问题你能确定圆形笑脸的圆心吗？利用三角板在圆中画出两个90°的圆周角，这样就得到两条直径，那么这两条直径的交点就是圆心. 如图，⊙O的直径AC为10cm，弦AD为6cm.（1）求DC的长；（2）若∠ADC的平分线交⊙O于B,求AB，BC的长．B解：(1)∵AC是直径，∴∠ADC=90°.在Rt△ADC中， 在Rt△ABC中，AB2+BC2=AC2，(2)∵AC是直径,∴∠ABC=90°.∵BD平∠ADC,∴∠ADB=∠CDB.又∵∠ACB=∠ADB,∠BAC=∠BDC.∴∠BAC=∠ACB,∴AB=BC.B解答圆周角有关问题时，若题中出现“直径”这个条件，则考虑构造直角三角形来求解.归纳 如图，BD是⊙O的直径，∠CBD＝30°，则∠A的度数为()A．30°B．45°C．60°D．75°解析：∵BD是⊙O的直径，∴∠BCD＝90°.∵∠CBD＝30°，∴∠D＝60°，∴∠A＝∠D＝60°.故选C.C练一练 1.如图，AB是⊙O的直径,C，D是圆上的两点,∠ABD=40°,则∠BCD=＿＿＿_.50°ABOCD2.如图，∠A=50°，∠ABC=60°，BD是⊙O的直径，则∠AEB等于（）A.70°B.110°C.90°D.120°BACBODE随堂练习 3.如图，△ABC内接于⊙O，AB=BC，∠ABC=120°，AD为⊙O的直径，AD=6，那么AB的值为（　　）A．3B．C．D．2A 4.如图，点A，B，D，E在⊙O上，弦AE，BD的延长线相交于点C.若AB是⊙O的直径，D是BC的中点．(1)试判断AB，AC之间的大小关系，并给出证明.解：(1)AB＝AC.证明如下：连接AD，∵AB是⊙O的直径，∴∠ADB＝90°，即AD⊥BC.∵BD＝DC，∴AD垂直平分BC，∴AB＝AC. (2)在上述题设条件下，当△ABC为正三角形时，点E是否为AC的中点？为什么？(2)当△ABC为正三角形时，E是AC的中点．理由如下：连接BE，∵AB为⊙O的直径，∴∠BEA＝90°，即BE⊥AC.∵△ABC为正三角形，∴AE＝EC，即E是AC的中点． 圆周角定理推论2推论3直径所所对的圆周角是直角；90°的圆周角所对的弦是直径课堂小结同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.