福建专版2020中考数学复习方案第三单元函数及其图象第12课时一次函数的应用课件
第12课时一次函数的应用第三单元 函数及其图象
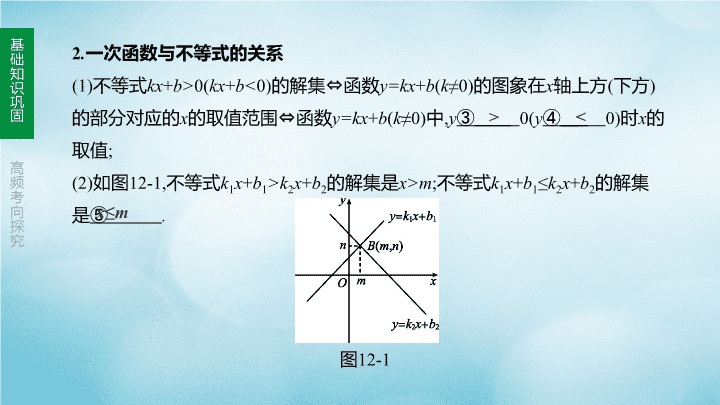
考点一 一次函数与一次方程(组)、一元一次不等式的关系考点聚焦图12-1x0
2.一次函数与不等式的关系(1)不等式kx+b>0(kx+b<0)的解集⇔函数y=kx+b(k≠0)的图象在x轴上方(下方)的部分对应的x的取值范围⇔函数y=kx+b(k≠0)中,y③0(y④0)时x的取值;(2)如图12-1,不等式k1x+b1>k2x+b2的解集是x>m;不等式k1x+b1≤k2x+b2的解集是⑤.>
4的解集为.x>-2图12-6
考向一 一次函数与一次方程(组)、一元一次不等式图12-7x=4x<4
|考向精练|1.若一次函数y=kx+b(k,b为常数,且k≠0)的图象过点A(0,-1),B(1,1),则不等式kx+b>1的解集为()A.x<0B.x>0C.x<1D.x>1D
图12-8A
图12-9
[答案]B
考向二 一次函数的应用(微专题)角度1方案决策例2[2019·德州]下表中给出A,B,C三种手机通话的收费方式.(1)设月通话时间为x小时,则方案A,B,C的收费金额y1,y2,y3都是x的函数,请分别求出这三个函数解析式.收费方式月通话费/元包时通话时间/时超时费/(元/分)A30250.1B50500.1C100不限时
(2)填空:若选择方式A最省钱,则月通话时间x的取值范围为;若选择方式B最省钱,则月通话时间x的取值范围为;若选择方式C最省钱,则月通话时间x的取值范围为.(3)小王、小张今年5月份通话费均为80元,但小王比小张通话时间长,求小王该月的通话时间.
例2[2019·德州]下表中给出A,B,C三种手机通话的收费方式.(2)填空:若选择方式A最省钱,则月通话时间x的取值范围为;若选择方式B最省钱,则月通话时间x的取值范围为;若选择方式C最省钱,则月通话时间x的取值范围为.收费方式月通话费/元包时通话时间/时超时费/(元/分)A30250.1B50500.1C100不限时
例2[2019·德州]下表中给出A,B,C三种手机通话的收费方式.(3)小王、小张今年5月份通话费均为80元,但小王比小张通话时间长,求小王该月的通话时间.收费方式月通话费/元包时通话时间/时超时费/(元/分)A30250.1B50500.1C100不限时(3)∵小王、小张今年5月份通话费均为80元,但小王比小张通话时间长,∴结合图象可得:小张选择的是方式A,小王选择的是方式B,∴6x-250=80,解得:x=55,∴小王该月的通话时间为55小时.
|考向精练|图12-10[2017·衢州]五一期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.根据以上信息,解答下列问题:(1)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,分别求出y1,y2关于x的函数表达式;(2)请你帮助小明计算并选择哪个出游方案合算.
解:(1)由题意可知y1=k1x+80,且图象过点(1,95),则有95=k1+80,∴k1=15,∴y1=15x+80(x≥0),由题意知y2=30x(x≥0).
图12-10[2017·衢州]五一期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.根据以上信息,解答下列问题:(2)请你帮助小明计算并选择哪个出游方案合算.
角度2费用和利润问题例3[2015·漳州]国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.(1)商店至多可以购买冰箱多少台?(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?类别彩电冰箱洗衣机进价(元/台)200016001000售价(元/台)230018001100
例3[2015·漳州]国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?类别彩电冰箱洗衣机进价(元/台)200016001000售价(元/台)230018001100
|考向精练|[2019·龙东地区]为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买2个甲种文具,1个乙种文具共需花费35元;购买1个甲种文具,3个乙种文具共需花费30元.(1)求购买一个甲种文具,一个乙种文具各需多少元?(2)若学校计划购买这两种文具共120个,投入资金不少于955元又不多于1000元,设购买甲种文具x个,求有多少种购买方案?(3)设学校投入资金w元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
[2019·龙东地区]为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买2个甲种文具,1个乙种文具共需花费35元;购买1个甲种文具,3个乙种文具共需花费30元.(2)若学校计划购买这两种文具共120个,投入资金不少于955元又不多于1000元,设购买甲种文具x个,求有多少种购买方案?(2)根据题意得955≤15x+5(120-x)≤1000,解得35.5≤x≤40,∵x是整数,∴x=36,37,38,39,40.∴有5种购买方案.
[2019·龙东地区]为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买2个甲种文具,1个乙种文具共需花费35元;购买1个甲种文具,3个乙种文具共需花费30元.(3)设学校投入资金w元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?(3)∵w=15x+5(120-x)=10x+600,∵10>0,∴w随x的增大而增大,当x=36时,w最小=10×36+600=960(元),∴120-36=84.答:购买甲种文具36个,乙种文具84个时投入资金最少,最少资金是960元.
角度3行程问题例4一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.两车行驶的时间为xh,两车之间的距离为ykm,图12-11中的折线表示y与x之间的函数关系,根据图象解决以下问题:(1)慢车的速度为km/h,快车的速度为km/h;(2)解释图中点C的实际意义并求出点C的坐标;(3)求当x为多少时,两车之间的距离为500km.图12-11
例4一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.两车行驶的时间为xh,两车之间的距离为ykm,图12-11中的折线表示y与x之间的函数关系,根据图象解决以下问题:(2)解释图中点C的实际意义并求出点C的坐标;图12-11(2)图中点C的实际意义是:快车到达乙地;∵快车走完全程所需时间为720÷120=6(h),∴点C的横坐标为6,纵坐标为(80+120)×(6-3.6)=480,即点C(6,480);
例4一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.两车行驶的时间为xh,两车之间的距离为ykm,图12-11中的折线表示y与x之间的函数关系,根据图象解决以下问题:(3)求当x为多少时,两车之间的距离为500km.图12-11
【方法点析】在读一次函数图象时,关键读几个点:(1)自变量和因变量是什么,代表的实际意义是什么;(2)图象的起始点、终止点与转折点分别在哪,坐标是什么,代表的实际意义是什么;(3)图象每一段的变化趋势,如果可以,接着判断趋势的缓急程度;(4)两个图象的交点坐标,代表的实际意义.
|考向精练|1.在某区创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图12-12是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?图12-12
1.在某区创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图12-12是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?图12-12
2.[2014·泉州]某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,B在AC上,甲的速度是乙的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2(米),则d1,d2与t的函数关系如图12-13所示,试根据图象解决下列问题:(1)填空:乙的速度v2=米/分;(2)写出d1与t的函数关系式;(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?图12-13解:(1)乙的速度v2=120÷3=40(米/分).
2.[2014·泉州]某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,B在AC上,甲的速度是乙的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2(米),则d1,d2与t的函数关系如图12-13所示,试根据图象解决下列问题:(2)写出d1与t的函数关系式;图12-13
2.[2014·泉州]某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,B在AC上,甲的速度是乙的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2(米),则d1,d2与t的函数关系如图12-13所示,试根据图象解决下列问题:(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?图12-13