2013山东烟台中考数学试题

2013山东烟台中考数学试题

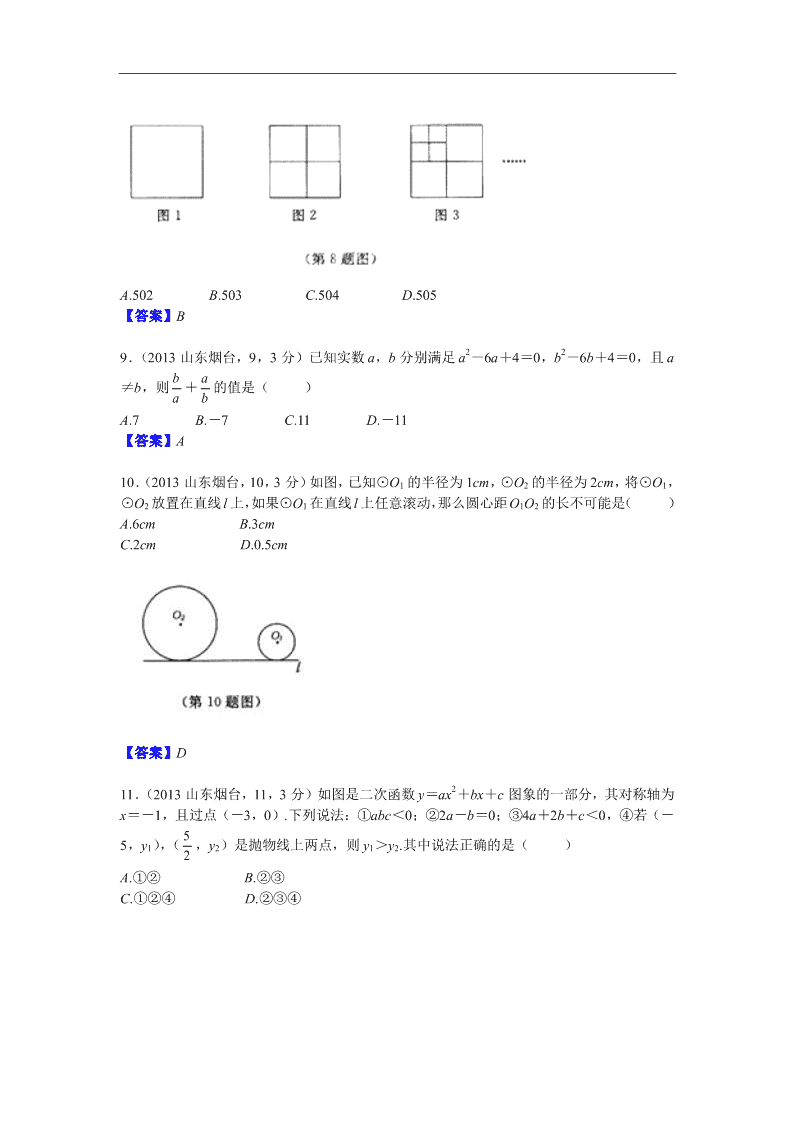
2013 年烟台市初中学生学业考试 数 学 试 题 说明： 1.本试题分为Ⅰ卷和Ⅱ卷两部分.第Ⅰ卷为选择题，第Ⅱ卷为非选择题.考试时间 120 分钟， 满分 120 分. 2.答题前将密封线内的项目填写清楚. 3.考试过程中允许考生进行剪、拼、折叠等实验. 第 Ⅰ 卷 注意事项： 请考生将自己的姓名、准考证号、考试科目涂写在答题卡上.选择题选出答案后，用 2B 铅笔 把答题卡对应题目的答案标号涂黑，不能答在本试题上.如要改动，必须先用橡皮擦干净， 再选涂另一个答案. 一、选择题（本题共 12 个小题，每小题 3 分，满分 36 分）每小题都给出标号为 A，B，C， D 四个备选答案，其中有且只有一个是正确的. 1．（ 2013 山东烟台，1，3 分）－6 的倒数是（ ） A. 1 6 B.－ 1 6 C.6 D.－6 【答案】B 2．（ 2013 山东烟台，2，3 分）以下是回收、绿色包装、节水、低碳四个标志，其中是中心 对称图形的是（ ） 【答案】B 3．（ 2013 山东烟台，3，3 分）“厉行勤俭节约，反对铺张浪费”势在必行.最新统计数据显 示，中国每年浪费食物总量折合为粮食大约是 210000000 人一年的口粮.将 210000000 用科 学记数法表示为（ ）. A.2.1×109 B.0.21×109 C.2.1×108 D.21×107 【答案】C 4．（ 2013 山东烟台，4，3 分）下列水平放置的几何体中，俯视图不是圆的是（ ） 【答案】C 5．（ 2013 山东烟台，5，3 分）下列各运算中，正确的是（ ） A.3a＋2a＝5a2 B.(－3a3) 2＝9a6 C.a6÷a2＝a3 D.(a＋2) 2＝a2＋4 【答案】B 6．（ 2013 山东烟台，6，3 分）如图，将四边形 ABCD 先向左平移 3 个单位，再向上平移 2 个单位，那么点 A 的对应点 A′的坐标是（ ） A.(0，1) B.(6，1) C.(0，－3) D.(6，－3) 【答案】A 7．（ 2013 山东烟台，7，3 分）一个多边形截去一个角后， 形成另一个多边形的内角和为 720°，那么原多边形的边数为（ ） A.5 B.5 或 6 C.5 或 7 D.5 或 6 或 7 【答案】D 8．（ 2013 山东烟台，8，3 分）将正方形图 1 作如下操作：第 1 次：分别连结各边中点如图 2，得到 5 个正方形；第 2 次：将图 2 左上角正方形按上述方法再分割如图 3，得到 9 个正 方形……，以此类推，根据以上操作，若要得到 2013 个正方形，则需要操作的次数是（ ） A.502 B.503 C.504 D.505 【答案】B 9．（ 2013 山东烟台，9，3 分）已知实数 a，b 分别满足 a2－6a＋4＝0，b2－6b＋4＝0，且 a ≠b，则 b a ＋ a b 的值是（ ） A.7 B.－7 C.11 D.－11 【答案】A 10．（ 2013 山东烟台，10，3 分）如图，已知⊙O1 的半径为 1cm，⊙O2 的半径为 2cm，将⊙O1， ⊙O2 放置在直线 l 上，如果⊙O1 在直线 l 上任意滚动，那么圆心距 O1O2 的长不可能是（ ） A.6cm B.3cm C.2cm D.0.5cm 【答案】D 11．（ 2013 山东烟台，11，3 分）如图是二次函数 y＝ax2＋bx＋c 图象的一部分，其对称轴为 x＝－1，且过点（－3，0）.下列说法：①abc＜0；②2a－b＝0；③4a＋2b＋c＜0，④若（－ 5，y1），（ 5 2 ，y2）是抛物线上两点，则 y1＞y2.其中说法正确的是（ ） A.①② B.②③ C.①②④ D.②③④ 【答案】C 12．（ 2013 山东烟台，12，3 分）如图 1，E 为矩形 ABCD 边 AD 上一点，点 P 从点 B 沿折 线 BE—ED—DC 运动到点 C 时停止，点 Q 从点 B 沿 BC 运动到点 C 时停止，它们运动的速 度都是 1cm／s.若点 P，Q 同时开始运动，设运动时间为 t(s)，△BPQ 的面积为 y(cm2).已知 y 与 t 的函数关系图象如图 2，则下列结论错误的是（ ） A.AE＝6cm B.sin∠EBC＝ 4 5 C.当 0＜t≤10 时，y＝ 2 5 t2 D.当 t＝12s 时，△PBQ 是等腰三角形 【答案】D 2013 年烟台市初中学生学业考试 数 学 试 题 题号 二 三 合计 13～18 19 20 21 22 23 24 25 26 得分 第 Ⅱ 卷 二、填空题（本题共 6 个小题，每小题 3 分，满分 18 分） 13．（ 2013 山东烟台，13，3 分）分解因式：a2b－4b3＝ . 【答案】b(a＋2b)(a－2b) 图 12-1 图 12-2 A D E P Q C B M N H y t O 10 14 40 14．（ 2013 山东烟台，14，3 分）不等式组 10 4 2 0 x x    的最小整数解是 . 【答案】x＝3 15．（ 2013 山东烟台，15，3 分）如图，四边形 ABCD 是等腰梯形，∠ABC＝60°，若其四 边满足长度的众数为 5，平均数为 25 4 ，上、下底之比为 1∶2，则 BD＝ . 【答案】5 3 16．（ 2013 山东烟台，16，3 分）如图，□ABCD 的周长为 36，对角线 AC，BD 相交于点 O， 点 E 是 CD 的中点，BD＝12，则△DOE 的周长为 . 【答案】15 17．（ 2013 山东烟台，17，3 分）如图，△ABC 中，AB＝AC，∠BAC＝54°，∠BAC 的平分 线与 AB 的垂直平分线交于点 O，将∠C 沿 EF（E 在 BC 上，F 在 AC 上）折叠，点 C 与点 O 恰好重合，则∠OEC 为 度. 【答案】108 18．（ 2013 山东烟台，18，3 分）如图，正方形 ABCD 的边长为 4，点 E 在 BC 上，四边形 EFGB 也是正方形，以 B 为圆心，BA 长为半径画AC⌒，连结 AF，CF，则图中阴影部分面积 为 . 【答案】4π 三、解答题（本大题共 8 个小题，满分 66 分） 19．（ 2013 山东烟台，19，6 分） 先化简，再求值： 224 4 1( 1)11 x x xxxx    ，其中 x 满足 x2＋x－2＝0. 解：原式＝ 2 2 ( 1)( 1) 1 1 4 4 1 x x x x x x x       ＝ 2 2 1 1 1 (2 1) xx xx  ＝ 1 12x . 由 x2＋x－2＝0，解得 x1＝－2，x2＝1. 由题意，得 x≠1，将 x＝－2 代入，原式＝ 1 5 . 20．（ 2013 山东烟台，20，6 分） 如图，一艘海上巡逻船在 A 地巡航，这时接到 B 地海上指挥中心紧急通知：在指挥中心北 偏西 60°方向的 C 地，有一艘渔船遇险，要求马上前去救援.此时 C 地位于 A 地北偏西 30° 方向上，A 地位于 B 地北偏西 75°方向上，A，B 两地之间的距离为 12 海里.求 A、C 两地之 间的距离.(参考数据： 2≈1.41， 3≈1.73， 6≈2.45，结果精确到 0.1.) 解：过点 B 作 BD⊥CA，交 CA 的延长线于点 D. 由题意，得∠ACB＝60°－30°＝30°， ∠ABC＝75°－60°＝15°, ∴∠DAB＝∠DBA=45°. 在 Rt△ADB 中，AB＝12，∠BAD＝45°， ∴BD＝AD＝ABcos45°＝6 2 . 在 Rt△BCD 中，CD＝ tan30 BD  ＝6 6 ∴AC＝6 －6 2 ≈6.2(海里) 答：A、C 两地之间的距离约为 6.2 海里. 21．（ 2013 山东烟台，21，7 分） 如图，在直角坐标中，矩形 OABC 的顶点 O 与坐标原点重合，A，C 分别在坐标轴上，点 B 的坐标为（4，2）直线 y＝－ 1 2 x＋3 交 AB，BC 分别于点 M，N，反比例函数 y＝ k x 的图象 经过点 M，N. （1）求反比例函数的解析式； （2）若点 P 在 y 轴上，且△OPM 的面积与四边形 BMON 的面积相等，求点 P 的坐标. 解：（1）由题意，得 OA＝BC＝2，将 y＝2 代入 y＝－ 1 2 x＋3，解得 x＝2，∴M(2，2). ∵反比例函数 y＝ 的图象经过点 M(2，2)，∴2＝ 2 k .∴k ＝4. ∴反比例函数的解析式 y＝ 4 x . （2）将 x=4 代入 y＝－ x＋3，解得 y=1. ∴N 点坐标为（4，1） ∵S 四边形 BMON＝S 矩形 OABC－S△AOM－S△NOC ＝4×2－2-2＝4. 由题意，得 1 2 OP·MA＝4，MA＝2， ∴OP＝4， ∴点 P 的坐标为(0，4)或(0，－4). 22．（ 2013 山东烟台，22，9 分） 今年以来，我国持续大面积的雾霾天气让环保和健康问题成为焦点，为了调查学生对雾霾天 气知识的了解程度，某校在学生中做了一次抽样调查，调查结果共分为四个等级： A、非 常了解；B、比较了解；C、基本了解；D、不了解.根据调查统计结果，绘制了不完整的三 种统计图表 请结合统计图表，回答下列问题. （1）本次参与调查的学生共有 人，m＝ ，n＝ ； （2）扇形统计图中 D 部分扇形所对应的圆心角是 度； （3）请补全条形统计图； （4）根据调查结果，学校准备开展关于雾霾知识竞赛，某班要从持“非常了解”态度的小 明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球 标上数字 1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另 一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数，则小明去； 否则小刚去.请用树状图或列表法说明这个游戏规则是否公平. 解：（1）400 15% 35% （2）126 （3）如图. （4）列表或树状图. 所以从树状图可以看出所有等可能的结果有 12 种，数字之和为奇数的有 8 种. ∴小明参加的概率 P＝ 8 12 ＝ 2 3 ，小刚参加的概率 P＝ 4 12 ＝ 1 3 . ∴游戏规则不公平. 23．（ 2013 山东烟台，23，8 分） 烟台享有“苹果之乡”的美誉.甲，乙两超市分别用 3000 元以相同的进价购进质量相同的苹 果. 甲超市销售方案是：将苹果按大小分类包装销售，其中大苹果 400 千克，以进价的 2 倍 价格销售，剩下的小苹果以高于进价的 10%销售.乙超市销售方案是：不将苹果按大小分类， 直接包装销售，价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完， 其中甲超市获利 2100 元（其它成本不计）. 问：（1）苹果进价为每千克多少元？ （2）乙超市获利多少元？并比较哪种销售方式更合算. 解：（1）设苹果进价为每千克 x 元. 由题意，得 400x＋10%x( 3000 x －400)＝2100， 解得 x＝5. 经检验 x＝5 是原方程的根. 答：苹果进价为每千克 5 元. （2）由（1）知：每个超市苹果总量： 3000 5 ＝600（千克）， 大、小苹果售价分别为 10 元和 5.5 元. ∴乙超市获利：600×(10 5.5 2  －5)＝1650（元）. ∵甲超市获利 2100＞1650，∴甲超市销售方式更合算. 24．（ 2013 山东烟台，24，8 分） 如图，AB 是⊙O 的直径，BC 是⊙O 的切线，连接 AC 交⊙O 于点 D，E 为 AD 上一点，连结 AE，BE，BE 交 AC 于点 F， 且 AE2=EF•EB. （1）求证：CB=CF； （2）若点 E 到弦 AD 的距离为 1，cos∠C= 3 5 ，求⊙O 的半 径. C B E A F O （第 24 题图） D （1）证明：∵AE2=EF•EB，∴ AE EB = EF AE 又∠AEF=∠AEB，∴△AEF∽△BEA. ∴∠4=∠5. ∵AB 是直径，BC 切⊙O 于点 B， ∴∠3+∠4=90°. 又∠1+∠5=90°. ∴∠1=∠3. ∵∠1=∠2，∴∠2=∠3. ∴CB=CF. （2）连结 OE 交 AC 于点 G. 由（1）知：∠4=∠5，∴ AE = ED . ∴OE⊥AD . ∴EG=1. ∵cos∠C= 3 5 ，且∠C+∠GAO=90°，∴sin∠GAO= . 设⊙O 的半径为 r，则 1r r  = ，解得 r= 5 2 . ∴圆半径为 . 25．（ 2013 山东烟台，25，10 分） 已知，点 P 是直角三角形 ABC 斜边 AB 上一动点（不与 A，B 重合）分别过点 A，B 向直线 CP 作垂线，垂足分别为 E，F，Q 为斜边 AB 的中点. （1）如图 1，当点 P 与点 Q 重合时，AE 与 BF 的位置关系是 ，QE 与 QF 的数 量关系是 ； （2））如图 2，当点 P 在线段 AB 上不与点 Q 重合时，试判断 QE 与 QF 的数量关系，并给 予证明； （3）如图 3，当点 P 在线段 BA（或 AB）的延长线上时，此时（2）中的结论是否成立？请 画出图形并给予证明. 解：（1）AE∥BF，QE＝QF. C B E A F O 1 2 3 4 5 （第 24 题） D （2）QE＝QF. 证明：延长 FQ 交 AE 于点 D. ∵AE∥BF，∴∠1＝∠2. ∵∠3＝∠4，AQ＝BQ， ∴△AQD≌△BQF . ∴QD＝QF. ∵AE⊥CP，∴QE 为斜边 FD 中线， ∴QE＝QF. （3）（ 2）中结论仍然成立. 理由：延长 EQ、FB 交于点 D， ∵AE∥BF，∴∠1＝∠D. ∵∠2＝∠3，AQ＝BQ， ∴△AQE≌△BQD.∴QE＝QD. ∵BF⊥CP，∴FQ 为斜边 DE 中线. ∴QE＝QF. 26．（ 2013 山东烟台，26，12 分） 如图，在平面直角坐标系中，四边形 OABC 是边长为 2 的正方形，二次函数 y＝ax2+bx+c 的图象经过点 A，B，与 x 轴分别交于点 E，F，且点 E 的坐标(－ 2 3 ，0)，以 OC 为直径作 半圆，圆心为 D. （1）求二次函数的解析式； （2）求证：直线 BE 是⊙O 的切线； （3）若直线 BE 与抛物线的对称轴交点为 P，M 是线段 CB 上的一个动点（点 M 与点 B，C 不重合），过点 M 作 MN∥BE 交 x 轴于点 N，连结 PM，PN，设 CM 的长为 t，△PMN 的面 积为 S，求 S 与 t 的函数关系式，并写出自变量 t 的取值范围.约 S 是否存在最大值？若存在， 求出最大值；若不存在，请说明理由. D O x y C B A E F P D O x y C B A E F 【答案】（1）由题意，得 A(0，2)，x＝－ 2 b a ＝1，E(－ 2 3 ，0)，∴ 2, 1,2 42 0,93 c b a a b c          解得 9 ,8 9 ,4 2, a b c        ∴二次函数的解析式为 y＝－ 9 8 x2+ 9 4 x+2. （2）过点 D 作 DG⊥BE 于点 G. 由题意，得 ED＝ 2 3 +1＝ 5 3 ，EC＝2+ ＝ 8 3 ，BC＝2， ∴BE＝ 64 49  ＝10 3 . ∵∠BEC＝∠DEG，∠EGD＝∠ECB＝90°， ∴△EGD∽△ECB. ∴ DG BC ＝ DE BE ，即 2 DG ＝ 5 3 10 3 ， ∴DG＝1. ∵⊙D 半径为 1，且 DG⊥BE， ∴BE 是⊙O 的切线，G 为切点. （3）由题意，得 E(－ 2 3 ，0)，B(2，2)， 设直线 BE 的解析式为 y＝kx+b， ∴ 2 2, 2 0,3 kb kb    解得 3 ,4 1 .2 k b     ∴直线 BE 的解析式为 y＝ 3 4 x+ 1 2 . ∵直线 BE 与对称轴交于点 P，对称轴为直线 x＝1， ∴y＝ 5 4 ，∴点 P 的坐标为(1， ). ∵MN∥BE，∴∠MNC＝∠BEC. ∵∠C＝∠C＝90°，∴△MNC∽△BEC. ∴ CN EC ＝ MC BC ，即 8 3 CN ＝ 2 t ， ∴CN＝ 4 3 t，∴DN＝ 4 3 t－1 D O x y C B A E F G 图 1 P D O x y C B A E F N M 图 2 ∴S△PND＝ 1 2 DN·PD＝ ·( 4 3 t－1)· 5 4 ＝ 5 6 t－ 5 8 ， S△MNC＝ CN·CM＝ · 4 3 t·t＝ 2 3 t2， S 梯形 PDCM＝ (PD+CM)·CD＝ ( 5 4 +t)·1＝ + t. ∵S＝S△PND+ S 梯形 PDCM－S△MNC ∴S＝－ t2+ t(0＜t＜2)， ∴S 存在最大值，当 t＝1 时，S 最大＝ .