中考数学一轮复习知识点+题型讲专题义01 有理数(学生版)
专题 01 有理数
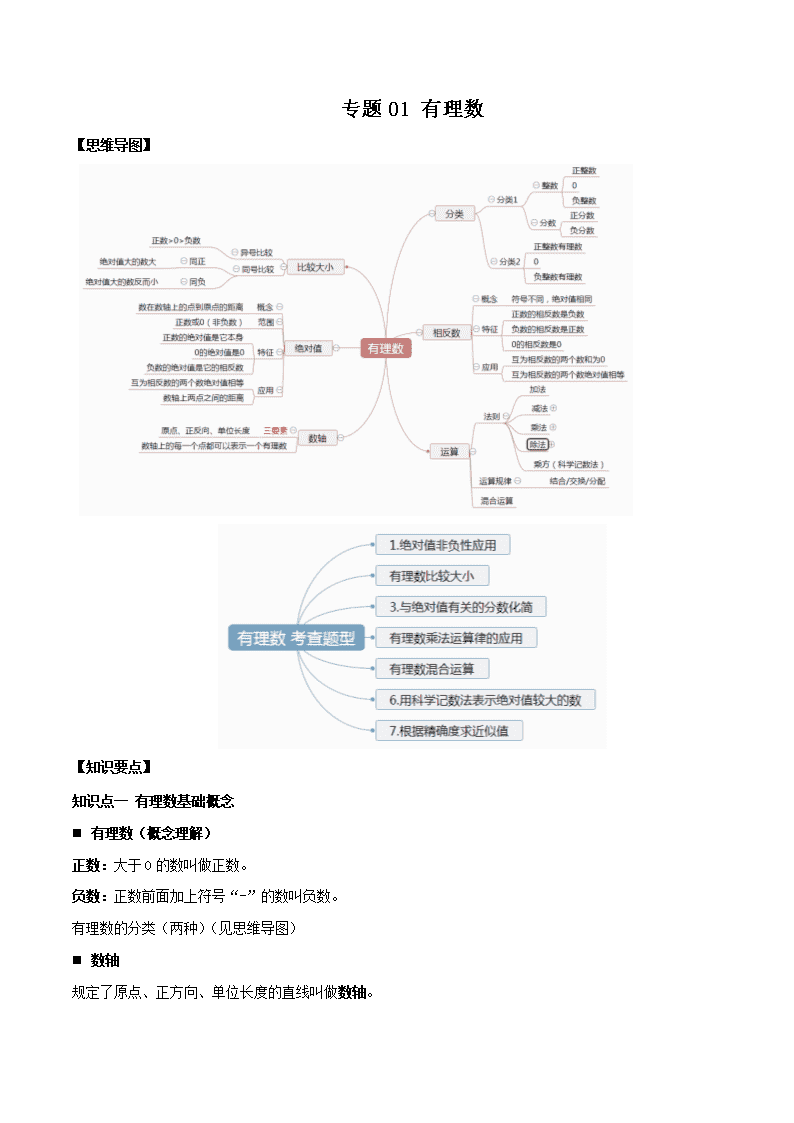
【思维导图】
【知识要点】
知识点一 有理数基础概念
有理数(概念理解)
正数:大于 0 的数叫做正数。
负数:正数前面加上符号“-”的数叫负数。
有理数的分类(两种)(见思维导图)
数轴
规定了原点、正方向、单位长度的直线叫做数轴。
数轴的三要素:原点、正方向、单位长度(重点)
任何有理数都可以用数轴上的点表示,有理数与数轴上的点是一一对应的。
数轴上的点表示的数从左到右依次增大;原点左边的数是负数,原点右边的数是正数.
【注意】
1. 数轴是一条直线,可向两段无限延伸。
2. 在数轴上原点,正方向,单位长度的选取需根据实际情况而定。
相反数
只有符号不同的两个数叫做互为相反数.(绝对值相等,符号不同的两个数叫做互为相反数)
绝对值
绝对值的概念:一班数轴上表示 a 的数与原点之间的距离叫做数 a 的绝对值。
绝对值的意义:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0 的绝对值是 0。
(互为相反数的两个数的绝对值相等。)
比较大小
1)数轴上两个点表示的数,右边的总比左边的大。
2)正数大于 0,负数小于 0,正数大于负数。
3)两个负数比较,绝对值大的反而小。
4)两个正数比较,绝对值大的反而大。
常用方法:数轴比较法、差值比较法、商值比较法、绝对值比较法等。
1.(2018·海南琼山中学中考模拟)下列各组数中,互为相反数的是 ( )
A.|+2|与|-2| B.-|+2|与+(-2) C.-(-2)与+(+2) D.|-(-3) |与-|-3|
2.(2019·四川中考真题) a 一定是
A.正数 B.负数 C. 0 D.以上选项都不正确
3.(2018·内蒙古中考模拟)如图,在数轴上表示互为相反数的两数的点是( )
A.点 A 和点 C B.点 B 和点 C C.点 A 和点 B D.点 B 和点 D
4.(2013·江苏中考真题)如图,数轴上的点 A、B 分别对应实数 a、b,下列结论中正确的是( )
A.a>b B.|a|>|b| C.﹣a<b D.a+b<0
5.(2019·甘肃中考真题)已知 1a ,b 是 2 的相反数,则 a b的值为( )
A.-3 B.-1 C.-1 或-3 D.1 或-3
考察题型一 绝对值非负性应用
1.(2016·山东中考真题)当 1
0, ,且 ,那么 x-y 的值是 ( )
A.2 或 12 B.2 或-12 C.-2 或 12 D.-2 或-12
4.(2018·浙江中考模拟)如果|a|≥0,那么( )
A.a>0 B.a<0 C.a≠0 D.a 为任意数
5.(2017·湖北中考模拟)若|x﹣2|+|y+2|=0,求 x﹣y 的相反数.
6.(2017·广东中考模拟)已知|a+3|+|b﹣5|=0,求:
(1)a+b 的值;
(2)|a|+|b|的值.
考查题型二 有理数比较大小
1.(2018·山东中考模拟)如果 a+b+c=0,且|a|>|b|>|c|.则下列说法中可能成立的是( )
A.b 为正数,c 为负数 B.c 为正数,b 为负数
C.c 为正数,a 为负数 D.c 为负数,a 为负数
2.(2019·北京中考模拟)实数 a,b,c 在数轴上的对应点的位置如图所示,如果 a+b=0,那么下列结论正
确的是( )
A.|a|>|c| B.a+c<0 C.abc<0 D. 0a
b
12.(2019·山东滨州市滨城区东城中学中考模拟)有理数 a,b 在数轴上的对应点如图所示,则下面式子中
正确的是( )
①b<0<a; ②|b|<|a|; ③ab>0; ④a﹣b>a+b.
A.①② B.①④ C.②③ D.③④
4.(2018·湖北中考真题)在 0,﹣1,0.5,(﹣1)2 四个数中,最小的数是( )
A.0 B.﹣1 C.0.5 D.(﹣1)2
5.(2018·山东中考真题)实数 a,b,c,d 在数轴上的位置如图所示,下列关系式不正确的是( )
A.|a|>|b| B.|ac|=ac C.b<d D.c+d>0
知识点二 有理数四则运算
有理数的加法(重点)
有理数的加法法则:(先确定符号,再算绝对值)
1.同号两数相加,取相同的符号,并把绝对值相加;
2.异号两数相加,绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
3.互为相反数的两个数相加得 0;(如果两个数的和为 0,那么这两个数互为相反数)
4.一个数同 0 相加,仍得这个数。
有理数的加法运算律:
加法交换律:两个数相加,交换加数的位置,和不变。
即 a b b a ;
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
即 a b c a b c 。
有理数的减法
有理数的减法法则:
减去一个数等于加上这个数的相反数。即 a b a b 。
注:两个变化:减号变成加号;减数变成它的相反数。
有理数的加减混合运算
规则:运用减法法则将加减混合运算统一为加法进行运算
步骤:(1)减法化加法;
(2)省略括号和加号;
(3)运用加法运算律使计算简便;
(4)运用有理数加法法则进行计算。
注:运用加法运算律时,可按如下几点进行:
(1)同号的先结合;
(2)同分母的分数或者比较容易通分的分数相结合;
(3)互为相反数的两数相结合;
(4)能凑成整数的两数相结合;
(5)带分数一般化为假分数或者分为整数和分数两部分,再分别相加。
有理数的乘法(重点)
有理数的乘法法则:
(1)两数相乘,同号得正,异号得负,并把绝对值相乘。
(2)任何数同 0 相乘,都得 0.
倒数:乘积是 1 的两个有理数互为倒数。0 没有倒数。(数 0a a 的倒数是
1
a )
多个有理数相乘的法则及规律:
(1) 几个不是 0 的数相乘,负因数的个数是奇数时,积是负数;
负因数的个数是偶数时,积是正数。
确定符号后,把各个因数的绝对值相乘。
(2)几个数相乘,有一个因数为 0,积为 0;反之,如果积为 0,那么至少有一个因数是 0.
注:带分数与分数相乘时,通常把带分数化成假分数,再与分数相乘。
有理数的乘法运算律
乘法交换律:两个数相乘,交换因数的位置,积相等。
即 a b b a 。
乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。
即 a b c a b c 。
乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加。
即 a b c a b a c 。
有理数的除法
有理数除法法则:
(1)除以一个不为 0 的数,等于乘以这个数的倒数。即 1 0a b a bb
。
(2)两数相除(被除数不为 0),同号得正,异号得负,并把绝对值相除。
0 除以任何不为 0 的数,都得 0。
步骤:先确定商的符号,再算出商的绝对值。
有理数的乘除混合运算
运算顺序:从左往右进行,将除法化成乘法后,进行约分计算。
(注:带分数应首先化为假分数进行运算)
有理数的四则混合运算
运算顺序:先乘除,后加减,有括号要先算括号里面的。
注:除法一般先化为乘法,带分数化为假分数,合理使用运算律
1.(2018·江苏中考模拟)计算:|–5+3|的结果是( )
A.–8 B.8 C.–2 D.2
2.(2019·浙江中考真题)某地一周前四天每天的最高气温与最低气温如右表,则这四天中温差最大的是
( )
星期 一 二 三 四
最高气温 10℃ 12℃ 11℃ 9℃
最低气温 3℃ 0℃ -2℃ -3℃
A.星期一 B.星期二 C.星期三 D.星期四
3.(2018·四川中考模拟)如果 a,b 是有理数,那么下列各式中成立的是( )
A.如果 a<0,b<0,那么 a+b>0 B.如果 a>0,b<0,那么 a+b>0
C.如果 a>0,b<0,那么 a+b<0 D.如果 a>0,b<0,且|a|>|b|,那么 a+b>0
4.(2019·辽宁中考模拟)计算 2 5( )7 7
的正确结果是( )
A. 3
7 B.- 3
7 C.1 D.﹣1
5.(2017·山东中考真题)计算-(-1)+|-1|,其结果为( )
A.-2 B.2 C.0 D.-1
6.(2018·辽宁中考模拟)两个非零有理数的和为零,则它们的商是( )
A.﹣1 B.0 C.1 D.﹣1 或 1
7.(2019·内蒙古中考模拟)若
�
�
�
的倒数与
� 倒 数
互为相反数,则
�
的值是( )
A.1 B.
� �
C.2 D.
� �8.(2018·天津中考模拟)-6÷ 1
6
的结果等于( )
A.1 B.﹣1 C.36 D.﹣36
8.(2019·平阳县鳌江中学中考模拟)-2×(-5)的值是 ( )
A.-7 B.7 C.-10 D.10
9.(2019·天津中考模拟)计算(–18)÷(–6)的结果等于
A.3 B.–3 C. 1
3 D.− 1
3
考查题型三 与绝对值有关的分数化简
1.(2018·福建中考模拟)若 a≠0,b≠0,则代数式
| | | | | |
a b ab
a b ab
的取值共有( )
A.2 个 B.3 个 C.4 个 D.5 个
2.(2018·南宫市奋飞中学中考模拟)已知 a,b,c 为非零的实数,则 a ab ac bc
a ab ac bc
的可能值的个数
为( )
A.4 B.5 C.6 D.7
3..(2019·四川初一期中)有理数 a,b.c 满足 abc<0, a b c abc
a b c abc
的值为( )
A.1 或﹣3 B.﹣4 C.0 D.0 或﹣4
考察题型四 有理数乘法运算律的应用
1.(2018·贵州中考真题)计算 1
2 + 1
6 + 1
12 + 1
20 + 1
30 +……+ 1
9900
的值为( )
A. 1
100 B. 99
100 C. 1
99 D. 100
99
2.(2019·河北中考模拟)利用运算律简便计算 52×(–999)+49×(–999)+999 正确的是( )
A.–999×(52+49)=–999×101=–100899
B.–999×(52+49–1)=–999×100=–99900
C.–999×(52+49+1)=–999×102=–101898
D.–999×(52+49–99)=–999×2=–1998
3.(2016·河北中考真题)请你参考黑板中老师的讲解,用运算律简便计算:
(1)999×(-15);
(2)999× 4118 5 +999×( 1
5
)-999× 318 5 .
知识点三 有理数的乘方
乘方(重点)
一般地, n 个相同的因数 a 相乘,即
� � � � �
⋯
� �� � ���� ����
个
,记作 na ,读作 a 的 n 次方。求 n 个相同因
数的积的运算,叫做乘方,乘方的结果叫做幂。
在 na 中, a 叫做底数, n 叫做指数。 na 读作 a 的 n 次方,也可以读作 a 的 n 次幂。
当底数为分数时,要先用括号将底数括上,再在其右上角写指数,指数要写的小些。
乘方的规律:
负数的奇次幂是负数,负数的偶次幂是正数。
正数的任何次幂都是正数,0 的任何正整数次幂都是 0.
有理数乘方的运算方法:
1. 根据乘方的符号规律确定结果的符号。
2. 计算结果的绝对值。
有理数的混合运算
运算顺序:(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先算括号里的,按小括号、中括号、大括号的顺序。
科学记数法
把一个大于 10 的数记成 10na 的形式,其中 a 是整数数位只有一位的数(即1 10a ), n 是
正整数,这样的记数方法叫科学记数法。(用科学记数法表示一个数时,10 的指数比原数的整数位数少 1.)
把 10na 还原成原数时,只需把 a 的小数点往前移动 n 位。
近似数和有效数字
在实际问题中,由“四舍五入”得到的数或大约估计的数都是近似数。(近似数小数点后的末位数是 0 的,
不能去掉 0.)
一个近似数从左边第一位非 0 的数字起,到末位数字止,所有的数字都是这个数的有效数字。一个近似数
有几个有效数字,就称这个近似数保留几个有效数字。
精确度:表示一个近似数与准确数的接近程度。一个近似数,四舍五入到哪一位,就称这个数精确到哪一
位。
1.(2018·丹东第九中学中考模拟)下列算式中,运算结果为负数的是( )
A.|-1| B.(-2)3 C.(-1)×(-2) D.(-3)2
2.(2018·四川成都外国语学校中考模拟)下列各数|﹣2|,﹣(﹣2)2,﹣(﹣2),(﹣2)3 中,负数的个数
有( )
A.1 个 B.2 个 C.3 个 D.4 个
3.(2018·河南中考模拟)若 a=﹣4×4,b=﹣|﹣32×1 2
3 |,c=﹣5+2(﹣22),则 a、b、c 的大小关系是( )
A.a>b>c B.c>b>a C.b>c>a D.c>a>b
考查题型五 有理数混合运算
1.(2018·湖北中考模拟)计算:
(1)5 1
4 -(-2 2
3
)+(-3 1
4
)-(+4 2
3
);
(2)(- 3 5 9
4 8 12
)×(-24);
(3)(-3)÷ 3
4 × 4
3 ×(-15);
(4)-14+|(-2)3-10|-(-3)÷(-1)2017.
2.(2018·湖北中考模拟)计算:
(1)﹣15+(﹣8)﹣(﹣11)﹣12
(2) 1 1 3 1( 3 ) ( ) ( )2 3 14 2
(3) 1 1 1 1( ) ( )36 6 9 3
(4)﹣23+[(﹣4)2﹣(1﹣32)×3]
3.(2018·海南琼山中学中考模拟) 2 31 1 3 1( ) ( ) 12 ( )3 3 4 6
考查题型六 用科学记数法表示绝对值较大的数
1.(2019·河南郑州实验外国语中学中考模拟)我国倡导的“一带一路”建设将促进我国与世界一些国家的互
利合作,根据规划“一带一路”地区覆盖总 人口为 4400000000 人,这个数用科学记数法表示为 ( )
A.44×108 B.4.4×108 C.4.4×109 D.4.4×1010
2.(2018·河南中考真题)今年一季度,河南省对“一带一路”沿线国家进出口总额达 214.7 亿元,数据“214.7
亿”用科学记数法表示为( )
A.2.147×102 B.0.2147×103 C.2.147×1010 D.0.2147×1011
3.(2019·安徽中考模拟)据资料显示,地球的海洋面积约为 360000000 平方千米,请用科学记数法表示地
球海洋面积面积约为多少平方千米( )
A. 736 10 B. 83.6 10 C. 90.36 10 D. 93.6 10
4.(2018·广东中考真题)260000000 用科学计数法表示为( )
A. 90.26 10 B. 82.6 10 C. 92.6 10 D. 726 10
5.(2019·山东中考模拟)一个整数 815550…0 用科学记数法表示为 8.1555×1010,则原数中“0”的个数为( )
A.4 B.6 C.7 D.10
考查题型七 根据精确度求近似值
1.(2018·山东中考模拟)近似数 3.02×106 精确到( )
A.百分位 B.百位 C.千位 D.万位
2.(2017·安徽中考模拟)用四舍五入法得到近似数 4.005 万,关于这个数有下列说法,其中正确的是( )
A.它精确到万位 B.它精确到 0.001
C.它精确到万分位 D.它精确到十位
3.(2019·山东中考模拟)近似数 1.23×103 精确到( )
A.百分位 B.十分位 C.个位 D.十位
4.(2019·福建中考模拟)30269 精确到百位的近似数是( )
A.303 B.30300 C. 330.2 30 D. 43.03 10
5.(2019·四川中考真题)用四舍五入法将130542精确到千位,正确的是( )
A.131000 B. 60.131 10 C. 51.31 10 D. 413.1 10
6.(2019·河北中考模拟)近似数 5.10 精确到( )
A.个位 B.十分位 C.百分位 D.十位
7.(2018·江苏中考模拟)今年无锡马拉松参赛选手 91879 人,这个数据精确到千位并用科学记数法表示为
( )
A.91×103 B.92×103 C.9.1×104 D.9.2×104
8.(2018·广西中考模拟)近似数 精确到( )
A.十分位 B.个位 C.十位 D.百位