2013山东枣庄中考数学试题

2013山东枣庄中考数学试题

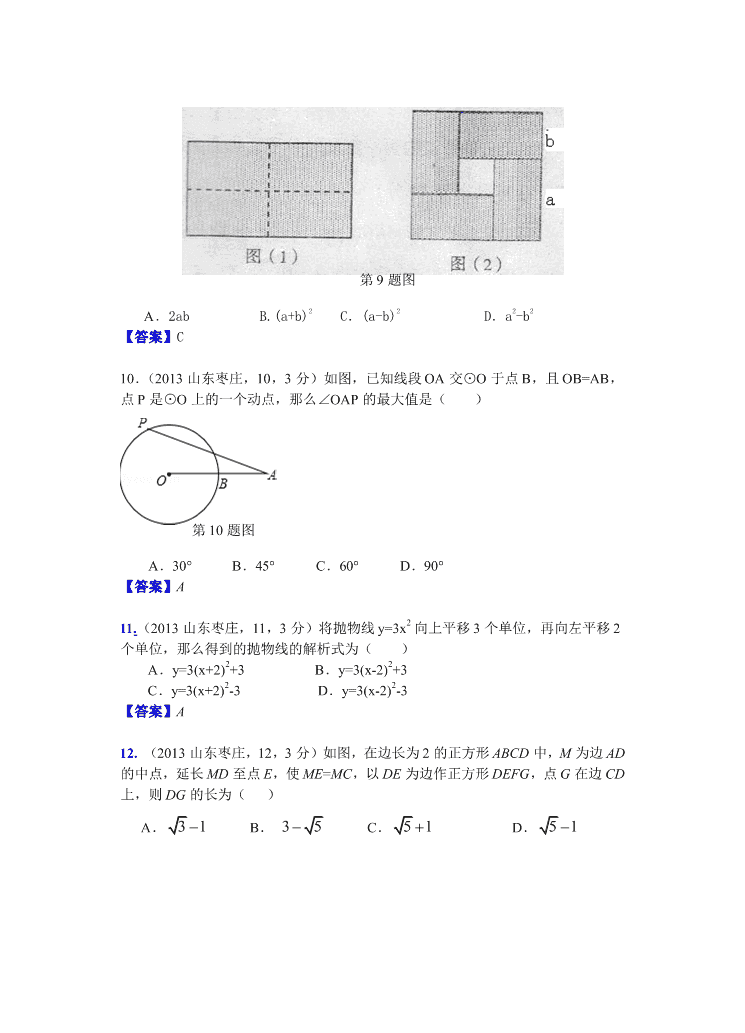
绝密☆启用前 试卷类型：A 二○一三年枣 庄 市 初 中 学 业考试 数 学 注意事项： 1．本试题分第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷为选择题，36 分；第Ⅱ卷为非选 择题，84 分；全卷共 6 页，满分 120 分．考试时间为 120 分钟． 2．答卷前，考生务必将自己的姓名、准考证号、考试科目和试卷类型涂写在 答题卡上，并把答题纸密封线内的项目填写清楚． 3．第Ⅰ卷每小题选出答案后，必须用 2B 铅笔把答题卡上对应题目的答案标号 (ABCD)涂黑．如需改动，先用橡皮擦干净，再改涂其它答案． 4. 第Ⅱ卷必须用黑色（或蓝色）笔填写在答题纸．．．的指定位置，否则不计分． 第Ⅰ卷 (选择题 共 36 分) 一、选择题：本大题共 12 小题，在每小题给出的四个选项中，只有一项是正确的， 请把正确的选项选出来．每小题选对得３分，选错、不选或选出的答案超过一个均 计零分． 1．（2013 山东枣庄，1，3 分）下列计算正确的是（ ）[中 A．－|－3|＝－3 B．30＝0 C．3－1＝－3 D． ＝±3 【答案】A 2．（2013 山东枣庄，2，3 分）如图，AB∥CD，∠CDE＝140°，则∠A 的度数为（ ） A．140° B．60° C．50° D．40° 【答案】D 3．（2013 山东枣庄，3，3 分）估计 61 的值在（ ） A．2 到 3 之间 B． 3 到 4 之间 C．4 到 5 之间 D．5 到 6 之间 第 2 题图 140° A B E C D 【答案】B 4．（2013 山东枣庄，4，3 分）化简 x x x x  11 2 的结果是（ ） A．x+1 B. x－1 C.—x D. x 【答案】D. 5．（2013 山东枣庄，5，3 分）某种商品每件的标价是 330 元，按标价的八折销售时， 仍可获利 10%，则这种商品每件的进价为 A．240 元 B．250 元 C．280 元 D．300 元 【答案】A． 6．（2013 山东枣庄，6，3 分）如图，△ ABC 中，AB=AC=10，BC=8，AD 平分∠BAC 交 BC 于点 D，点 E 为 AC 的中点，连接 DE，则△ CDE 的周长为（ ） A．20 B． 12 C．14 D． 13 【答案】C 7. （2013 山东枣庄，7，3 分）若一元二次方程 x2＋2x＋m＝0 有实数根，则 m 的取 值范围是（ ） A．m≤－1 B．m≤1 C．m≤4 D．m≤ 2 1 【答案】B 8. （2013 山东枣庄，8，3 分）对于非零的两个实数 a、b，规定 abba 11  ， 若 1)12(2  x ，则 x 的值为（ ） A． 6 5 B． 4 5 C． 2 3 D． 6 1 【答案】A 9. （2013 山东枣庄，9，3 分）图（1）是一个长为 2a，宽为 2b（a>b）的长方形， 用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形， 然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（ ） 第 6 题图 A．2ab B.(a+b)2 C．(a-b)2 D．a2-b2 【答案】C 10．（2013 山东枣庄，10，3 分）如图，已知线段 OA 交⊙O 于点 B，且 OB=AB， 点 P 是⊙O 上的一个动点，那么∠OAP 的最大值是（ ） A．30° B．45° C．60° D．90° 【答案】A 11.（2013 山东枣庄，11，3 分）将抛物线 y=3x2 向上平移 3 个单位，再向左平移 2 个单位，那么得到的抛物线的解析式为（ ） A．y=3(x+2)2+3 B．y=3(x-2)2+3 C．y=3(x+2)2-3 D．y=3(x-2)2-3 【答案】A 12. （2013 山东枣庄，12，3 分）如图，在边长为 2 的正方形 ABCD 中，M 为边 AD 的中点，延长 MD 至点 E，使 ME=MC，以 DE 为边作正方形 DEFG，点 G 在边 CD 上，则 DG 的长为（ ） A． 31 B． 35 C． 51 D． 51 第 9 题图 第 10 题图 【答案】D 第Ⅱ卷 (非选择题 共 84 分) 二、填空题：本大题共 6 小题，满分 24 分．只要求填写最后结果，每小题填对得 4 分． 13. （2013 山东枣庄，13，4 分）若 a2-b2= 1 6 ，a-b= 1 3 ，则 a+b 的值为 【答案】 1 2 14. （2013 山东枣庄，14，4 分）在方格纸中，选择标有序号①②③④中的一个小 正方形涂黑，与图中阴影部分构成中心对称图形，该小正方形的序号是 ． 【答案】② 15. （2013 山东枣庄，15，4 分）从 1、2、3、4 中任取一个数作为十位上的数字， 再从 2、3、4 中任取一个数作为个位上的数字，那么组成的两位数是 3 的倍数的概 率是 ． 【答案】 1 3 16. （2013 山东枣庄，16，4 分）从棱长为 2 的正方体毛坯的一角，挖去一个棱长 为 1 的小正方体，得到一个如图 5 所示的零件，则这个零件的表面积是 . ① ② ③ ④ 第 14 题图 第 12 题图 【答案】24 17.（2013 山东枣庄，17，4 分）若正比例函数 y=－2x 与反比例函数 y= x k 图象的一 个交点坐标为(－1,2)，则另一个交点的坐标为 ． 【答案】(1，－2) 18.（2013 山东枣庄，18，4 分）如图，已知矩形 ABCD 中，AB=1，在 BC 上取一点 E，沿 AE 将△ABE 向上折叠，使 B 点落在 AD 上的 F 点，若四边形 EFDC 与矩形 ABCD 相似，则 AD= ． 【答案】 51 2  三、解答题：本大题共 7 小题，满分 60 分．解答时，要写出必要的文字说明、证 明过程或演算步骤． 19. （2013 山东枣庄，19，8 分）先化简，再求值： 2 35( 2 )3 6 2 m mm m m     ， 其中 m 是方程 x2＋3x－1＝0 的根． 【解】∵m 是方程 x2＋3x－1＝0 的根，∴m2＋3m－1＝0，即 m2＋3m＝1． ∴所求式＝ 3 ( 2)( 2) 5 3 ( 2) 2 m m m m m m     ＝ 32 3 ( 2) ( 3)( 3) mm m m m m    ＝ 1 3 ( 3)mm ＝ 2 1 3( 3 )mm ＝ 1 3 ． 20. （2013 山东枣庄，20，8 分）图 1、图 2 是两张形状、大小完全相同的方格纸， 方格纸中的每个小正方形的边长均为 1，点 A、B 在小正方形的顶点上． （1）在图 1 中画出△ABC（点 C 在小正方形的顶点上），使△ABC 为直角三角形 F E D CB A 第 18 题图 第 16 题图 （画一个即可）． （2）在图 2 中画出△ABD（点 D 在小正方形的顶点上），使△ABD 为等腰三角形 （画一个即可）． 【解】解：（1）正确画图（参考图 1-图 4，画出一个即可）． （2）正确画图（参考图 5-图 8，画出一个即可）． 21. （2013 山东枣庄，21，8 分）“六·一”前夕，质检部门从某超市经销的儿童玩 具、童车和童装中共抽查了 300 件儿童用品﹒以下是根据抽查结果绘制的不完整的 统计表和扇形图： 请你根据上述统计表和扇形图提供的信息，完成下列问题： ⑴分别补全上述统计表和扇形图； ⑵已知所抽查的儿童玩具、童车、童装的合格率分别为 90%、88%、80%﹒若从该 类别 儿童玩具 童车 童装 抽查件数 90 童车 25% 儿童玩具 % 童装 % 第 21 题图 第 20 题图 超市的这三类儿童用品中随机购买一件，请估计能买到合格品的概率是多少？ 【解】 ⑴ ⑵ 85.0300 %80135%8875%9090  22. （2013 山东枣庄，22，8 分）校车安全是近几年社会关注的重大问题，安全隐 患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度 的实验：先在公路旁边选取一点 C，再在笔直的车道 l 上确定点 D，使 CD 与 l 垂直， 测得 CD 的长等于 21 米，在 l 上点 D 的同侧取点 A、B，使 ∠CAD=30°，∠CBD=60°． （1）求 AB 的长（精确到 0.1 米，参考数据： 3 =1.73， 2 =1.41）； （2）已知本路段对校车限速为 40 千米／小时，若测得某辆校车从 A 到 B 用时 2 秒， 这辆校车是否超速？说明理由． 【解】解：（1）由题意得，在 Rt△ADC 中，AD= tan30 CD  = 21 3 3 =21 3 =36.33，在 Rt△BDC 中，BD= tan 60 CD  = 21 3 = 73=12.11， 所 以 AB=AD - BD=36.33 – 12.11=24.22≈24.2（米）． （2）校车从 A 到 B 用时 2 秒，所以速度为 24.2÷2=12.1（米／秒），因为 12.1×3600=43560，所以该车速度为 43,56 千米／小时，大于 40 千米／小时，所以 此校车在 AB 路段超速． 23. （2013 山东枣庄，23，8 分）如图，在平面直角坐标系中，直角梯形 OABC 的 类别 儿童玩具 童车 童装 抽查件数 90 75 135 lD C BA 第 22 题图 童车 25% 儿童玩具 30% 童装 45% 边 OC、OA 分别与 x 轴、y 轴重合，AB∥OC，∠AOC=90°，∠BCO=45°，BC=12 2 ， 点 C 的坐标为（-18，0）． （1）求点 B 的坐标； （2）若直线 DE 交梯形对角线 BO 于点 D，交 y 轴于点 E，且 OE=4，OD=2BD， 求直线 DE 的解析式； 【解】解：（1）过点 B 作 BF⊥x 轴于 F，如图． 在 Rt△ BCF 中，∵ ∠BCO=45°，BC=6 2 ，∴ CF=BF=12．∵C 的坐标为(-18， 0)，∴AB=OF=6，∴ 点 B 的坐标为（-6，12）； （2）过点 D 作 DG⊥y 轴于点 G，如图． ∵AB∥DG，∴△ODG∽△OBA．∵DG AB =OD OB =OG OA =2 3 ，AB=6，OA=12，∴DG=4， 第 23 题图 OG=8，∴D(-4，8)，E(0，4)．设直线 DE 解析式为 y=kx＋b(k≠0)，得 48 4 kb b      ， 1 4 k b    ，∴直线 DE 解析式为 y=-x＋4； 24. （2013 山东枣庄，24，10 分）如图，AB 是⊙O 的直径，AC 是弦，直线 EF 经 过点 C，AD⊥EF 于点 D，∠DAC=∠BAC． ⑴求证 EF 是⊙O 的切线； ⑵求证 AC2=AD·AB ⑶若⊙O 的半径为 2，∠ACD=30°，求图中阴影部分的面积． 【解】⑴证明：连接 OC，∵AD⊥EF ∴∠ADC=90°， ∴∠ACD+∠CAD=90°， ∵OC=OA，∴∠ACO=∠CAO， ∵∠DAC=∠BAC ∴∠CAD=∠ACO， ∵∠ACD+∠CAD=90°， ∴∠ACD+∠ACO =90°即∠OCD=90°， ∴EF 是⊙O 的切线 ⑵证明：连接 BC． ∵CD 是⊙O 的切线，∴∠OCD=90°， 即∠ACD+∠ACO=90°．…① ∵OC=OA，∴∠ACO=∠CAO， ∴∠AOC=180°-2∠ACO，即 1 2 ∠AOC+∠ACO=90°. ② ，由①，②，得： ∠ACD- 1 2 ∠AOC=0，即∠AOC=2∠ACD；∵∠AOC=2∠B，∴∠B=∠ACD， ∵AB 是直径，∴∠ACB=∠ADC=90°．在 Rt△ACD 与△RtACB 中，∵∠B=∠ACD ∠ACB=∠ADC，∴△ACD∽△ABC，∴ AC AD AB AC ，即 AC2=AB·AD． 第 24 题图 ⑶∵CD 是⊙O 的切线，∴∠OCD=90°， 即∠ACD+∠ACO=90°，∵∠ACD=30°， ∴∠OCA=60°，∵OC=OA，∴△ACO 是等边三角形，∴AC= OC=2，∠AOC=60°， 在 Rt△ADC 中，∵∠ACD=30°，∴AD=1，CD= 3 ， S 阴影= S 梯形 OCDA- S 扇形 OCA= 21 60 2 3 3 2(1 2) 32 360 2 3      ． 25. （2013 山东枣庄，25，10 分）如图，在平面直角坐标系中，二次函数 2= + +y x bx c 的图象与 x 轴交于 A、B 两点，B 点的坐标为(3,0)，与 y 轴交于 C(0，－3)，点 P 是 直线 BC 下方抛物线上的动点． （1）求这个二次函数的解析式； （2）连接 PO、PC，并将△POC 沿 y 轴对折，得到四边形 POP’C，那么是否存在 点 P，使得四边形 POP’C 为菱形？若存在，求出此时点 P 的坐标；若不存在，请说 明理由； （3）当点 P 运动到什么位置时，四边形 ABPC 的面积最大？求出此时 P 点的坐标 和四边形 ABPC 的最大面积． 【解】解：(1)将 B、C 两点的坐标代入 得 3 + =-9 =-3 bc c    ，解得 =-2 =-3 b c    ． ∴这个二次函数的解析式为：y=x2-2x-3． (2)假设抛物线上存在点 P(x, x2-2x-3)，使得四边形 POP’C 为菱形．连接 PP’交 CO 于点 E．∵四边形 POP’C 为菱形，∴PC＝PO，PE⊥CO，∴OE＝EC＝ 3 2 ，∴P 点的纵坐标为 3- 2 ，即 x2-2x-3＝ 3- 2 ，解得 12 2+ 10 2- 10==22xx， （不合题 第 25 题图 第 25 题备用图 意，舍去）．∴存在点 P( 2+ 10 2 ， 3- 2 )，使得四边形 POP’C 为菱形． (3)过点 P 作 y 轴的平行线交 BC 于点 Q，交 OB 于点 F，设 P(x, x2-2x-3)．由 x2-2x-3 ＝0 得点 A 的坐标为(－1,0)．∵B 点的坐标为(3,0)，C 点的坐标为(0，－3)，∴直线 BC 的解析式为：y＝x－3，∴Q 点的坐标为(x，x－3)，∴AB＝4，CO＝3，BO＝3， PQ＝-x2+3x．∴S 四边形 ABPC＝S△ABC＋ S△BPQ ＋ S△CPQ ＝ 1 2 AB·CO＋ 1 2 PQ·BF＋ 1 2 PQ·FO ＝ AB·CO ＋ PQ·(BF ＋FO)＝ AB·CO ＋ PQ·BO ＝ 1 2 ×4×3 ＋ 1 2 ( 2- +3xx)×3＝ 239- + 622xx ＝ 23 3 75- ( ) +2 2 8x  ． ∴当 x＝ 3 2 时，四边形 ABPC 的面积最大．此时 P 点的坐标为( , 15- 4 )，四边形 ABPC 的最大面积为 75 8 ．