2019年四川省广元市中考真题数学试题(解析版)0
2019 年四川省广元市中考数学试卷
一、选择题(本大题共 10 小题,每小题 3 分,共 30 分)
1(2019 年广元 1) -8 的相反数是( )
A. B.-8 C.8 D.
2(2019 年广元 2.)下列运算中正确的是( )
A. B. C. D.
3(2019 年广元 3.)函数 的自变量 的取值范围是( )
A. B. C. D.
4(2019 年广元 4.)如果一组数据 的平均数是 ,那么这组数据的中位数为( )
A.5 B.6 C.7 D.9
5(2019 年广元 5.)我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个
圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形
成“牟合方盖”的一种模型,它的俯视图是( )
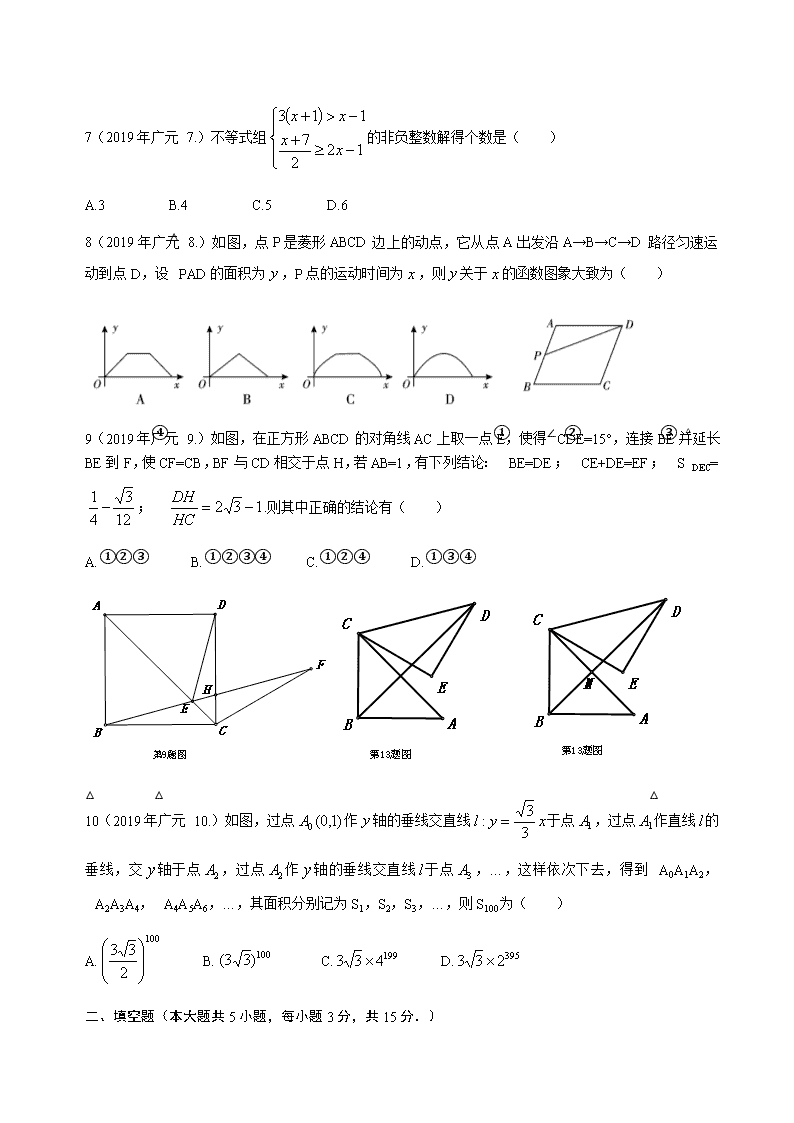
6(2019 年广元 6.)如图,AB,AC 分别是⊙O 的直径和弦,OD⊥AC 于点 D,连接 BD,BC,且
AB=10,AC=8,则 BD 的长为( )
A. B.4 C. D.4.8
8
1−
8
1
1055 aaa =+ 67 aaa =÷ 623 aaa =⋅ 623 )( aa −=−
1−= xy x
1>x 1
+
122
7
113
xx
xx
y x y x
12
3
4
1 − 132 −=
HC
DH
)1,0(0A y xyl 3
3: = 1A 1A l
y 2A 2A y l 3A
100
2
33
100)33( 199433 × 395233 ×
11(2019 年广元 11.)分解因式: .
12(2019 年广元 12.)若关于 的一元二次方程 有两个不相等的实数根,则点
在第 象限.
13(2019 年广元 13.)如图,△ABC 中,∠ABC=90°,BA=BC=2,将△ABC 绕点 C 逆时针旋转 60°得到△DEC,
连接 BD,则 的值是.
14(2019 年广元 14.)如图,△ABC 是⊙O 的内接三角形,且 AB 是⊙O 的直径,点 P 为⊙O 上的动点,
且∠BPC=60°,⊙O 的半径为 6,则点 P 到 AC 距离的最大值是.
15(2019 年广元 15.)如图,抛物线 过点(-1,0),(0,2),且顶点在第一象限,
设 ,则 的取值范围是.
三、解答题(共 75 分)要求写出必要的解答步骤或证明过程.
16(2019 年广元 16.)(6 分)计算:
17(2019 年广元 17.)先化简: ,再从 1,2,3 中选取一个适当的数代入求值.
第14题图
C
B
O
A
P
F
P
C
B
O
A
=− aa 43
x )0(04
12 ≠=−− axax
)3,1( −−+ aaP
2BD
)0(2 ≠++= acbxaxy
cbaM ++= 24 M
°+−−−+− − 30tan3)3
1()2019(23 10π
44
1)11
3( 2 +−
−⋅−−− xx
xxx
18(2019 年广元 18.)(6 分)如图,已知:在△ABC 中,∠BAC=90°,延长 BA 到点 D,使 AD= AB,
点 E,F 分别是边 BC,AC 的中点.求证:DF=BE.
19(2019 年广元 19.)(8 分)如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要
的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开
水,B.瓶装矿泉水,C.碳酸饮料,D 非碳酸饮料。根据统计结果绘制如下两个统计图,根据统计图提供
的信息,解答下列问题:
(1)这个班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种只限一瓶,价格如下表),则该班同学每天用于饮品的
人均花费是多少元?
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的 5 名班委干部(其中有两位班长记为 A,B,
其余三位记为 C,D,E)中随机抽取 2 名班委干部作为良好习惯监督员,请用列表法或画树状图的方法
求出恰好抽到两位班长的概率。
2
1
20(2019 年广元 20.)(8 分)某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比
乙种水果的进价每千克少 4 元,且用 800 元购进甲种水果的数量与用 1000 元购进乙种水果的数量相同。
(1)求甲、乙两种水果的单价分别是多少元?(2)该水果商根据该水果店平常的销售情况确定,购进两种
水果共 200 千克,其中甲种水果的数量不超过乙种水果数量的 3 倍,且购买资金不超过 3420 元,购回后,
水果决定甲种水果的销售价定为每千克 20 元,乙种水果的销售价定为每千克 25 元,则水果商应如何进
货,才能获得最大利润,最大利润是多少?
21(2019 年广元 21.)(8 分)如图,某海监船以 60 海里/时的速度从 A 处出发沿正西方向巡逻,一可疑
船只在 A 的西北方向的 C 处,海监船航行 1.5 小时到达 B 处时接到警报,需巡查此可疑船只,此时可疑
船只仍在 B 的北偏西 30°方向的 C 处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速 90
海里/时的速度追击,在 D 处海监船追到可疑船只,D 在 B 的北偏西 60°方向(以下结果保留根号)
(1)求 B,C 两处之间的距离;(2)求海监船追到可疑船只所用的时间。
22(2019 年广元 22.)(10 分)如图,平面直角坐标系中,直线 AB 与 轴交于点 B(0,7),与反比例
函数 在第二象限内的图象相交于点 A(﹣1,α)。(1)求直线 AB 的解析式;(2)将直线 AB 向下
平移 9 个单位后与反比例函数的图象交于点 C 和点 E,与 轴交于点 D,求△ACD 的面积;(3)设直线 CD
的解析式为 ,根据图象直接写出不等式 的解集。
第21题图
E
F
D C
AB
y
xy 8−=
y
nmxy +=
xnmx 8−≤+
23(2019 年广元 23. )(10 分)如图,AB 是⊙O 的直径,点 P 是 BA 延长线上一点,过点 P 作
⊙O 的切线 PC,切点是 C,过点 C 作弦 CD AB 于点 E,连接 CO,CB。
(1)求证:PD 是⊙O 的切线;
(2)若 AB=10,anB= ,求 PA 的长;
(3)试探究线段 AB,OE,OP 之间的数量关系,并说明理由。
24(12 分)如图,直线 与 轴, 轴分别交于 A,B 两点,过 A,B 两点的抛物线
与 轴交于 C(-1,0)。
(1)求抛物线的解析式;
(2)连接 BC,若点 E 是线段 AC 上的一个动点(不与 A,C 重合),过点 E 作 EF//BC,交 AB 于点 F,
当△BEF 的面积是 时,求点 E 的坐标;
(3)在(2)的结论下,将△BEF 绕点 F 旋转 180°得△B´E´F´,试判断点 E´是否在抛物线上,并说明理
⊥
2
1
4+−= xy x y
cbxaxy ++= 2 x
2
5
由。
2019 年四川省广元市中考数学试卷
(满分120 分,考试时间120 分钟)
一、选择题(本大题共 10 小题,每小题 3 分,共 30 分.在每小题给出的 4 个选项中,只有一个是正确
的,每小题选对得 3 分,选错、不选或多选均不得分)
(2019 年广元 1.) -8 的相反数是( )
A. B.-8 C.8 D.
{答案}C
{解析}本题考查了相反数的定义,只有符号不同的两个数叫做互为相反数,因此本题选 C.
(2019 年广元 2.)下列运算中正确的是( )
A. B. C. D.
{答案}B
{解析}本题考查了整式运算, A 项考查的是整式的加法就是合并同类项,要合并它们的系数,字母和字
母指数不变, 所以 A 项是错误的; B 项考察同底数幂相除,底数不变,指数相加减,结果正确; C 项
考查的是同底数幂的除法,底数不变,指数相加,所以 C 项是错误的; D 项考查了积的乘方,要将积中
每个因式分别乘方,其中(-1)2=1,所以 D 项是错误的。
(2019 年广元 3.)函数 的自变量 的取值范围是( )
A. B. C. D.
{答案}D
{解析}本题考查了二次根式的有意义的条件,是被开方数≥0。由 x-1≥0 得,x≥1。所以选 D。
8
1−
8
1
1055 aaa =+ 67 aaa =÷ 623 aaa =⋅ 623 )( aa −=−
1−= xy x
1>x 1+
122
7
113
xx
xx
y x y x
12
3
4
1 − 132 −=
HC
DH
{答案}A
{解析}本题考查了正方形的性质。∵点 E 在正方形 ABCD 的对角线 AC 上,易得△BCE≌△DCE,∴
BE=DE,故①正确;如图 2,在 EF 上截取 EG=EC,连接 CG。由△BCE≌△DCE 可得∠CBE=∠
CDE=15°,又∵∠ECB=45°,∴∠CEF=60°,∴△ECG 是等边三角形,∴∠ECG=60°,EC=CG;在△BCF
中,∵CF=CB,∠CBE =15°,∴∠BCF=150°,∴∠GCF=45°,∴∠ECD=∠GCF=45°,可证得△DCE≌△
FCG,∴DE=GF,∴DE+CE=GF+EG=EF,故②正确;如图 3,作∠DEQ =15°,交 CD 于点 Q,过点 E
作 ER⊥CD 于点 R,易得 DQ=EQ,∠EQR =30°,设 ER=x,则 CR=x,QR= x,EQ=DQ=2x,由
CR+RQ+QD=1 可解得 x= ∴S△DEC= = ,故③正确;如图 2 中可求得∠
DEH=60°,∴∠DEH=∠CEH=60°,从而可证得 ,如图 3,EC= x,DE=( )x,∴
,故④错误,∴选 A。
第9题图
H
F
E
B C
A D
第9题图2
H G
F
E
B C
DA
第9题图3
R
Q
E
B C
DA
12
3
4
1 −
DH DE
HC EC
= 2 6 2+
6 2 3 1
2
DH DE
HC EC
+= = = +
(2019 年广元 10.)如图,过点 作 轴的垂线交直线 于点 ,过点 作直线 的垂
线,交 轴于点 ,过点 作 轴的垂线交直线 于点 ,…,这样依次下去,得到△A 0A1A2,
△A2A3A4,△A4A5A6,…,其面积分别记为 S1,S2,S3,…,则 S100 为( )
A. B. C. D.
{答案}D
{解析}本题考查了寻找相似三角形面积的规律问题。由题可知,△A0A1A2,△A2A3A4,△A4A5A6,…,都
相似,且相似比为 4,计算出△A0A1A2 的面积为 ,则 S100 为
{题型:2-填空题}二、填空题(本大题共 5 小题,每小题 3 分,共 15 分.把正确答案直接填写在答题卡上
对应题目的横线上)
(2019 年广元 11.)分解因式: .
{答案}a(a+2)(a-2)
{解析}本题考查了因式分解法中的提公因式法和平方差公式,先提公因式 a,然后再用平方差公式进行分
解。
(2019 年广元 12.)若关于 的一元二次方程 有两个不相等的实数根,则点
在第 象限.
{答案}四
{解析}本题考查了一元二次方程根的判别式,以及象限内点的坐标特点。因为方程有两个不相等的实数
根,所以△>0 即 1-4a(- )>0,解得 a>-1;所以 a+1>0,-a-3<0,所以点 P 在第四象限。
)1,0(0A y xyl 3
3: = 1A 1A l
y 2A 2A y l 3A
100
2
33
100)33( 199433 × 395233 ×
3 3
2
( )992 3953 3 4 3 3 22
× = ×
=− aa 43
x )0(04
12 ≠=−− axax
)3,1( −−+ aaP
1
4
(2019 年广元 13.)如图,△ABC 中,∠ABC=90°,BA=BC=2,将△ABC 绕点 C 逆时针旋转 60°得到
△DEC,连接 BD,则 的值是.
{答案}
{ 解 析 } 本 题 考 查 解 直 角 三 角 形 。 设 AC 与 BD 交 于 点 M 。 由 题 易 得 CM ⊥ BD , 由 旋 转 可 得
CD=CA= ,∠MCD=60°,所以 MD= ;在 R△BCM 中,∠MCB=45°,BC=2,所以 BM= ;所以
BD= ,BD2= =
(2019 年广元 14.)如图,△ABC 是⊙O 的内接三角形,且 AB 是⊙O 的直径,点 P 为⊙O 上的动点,
且∠BPC=60°,⊙O 的半径为 6,则点 P 到 AC 距离的最大值是.
{答案}
{解析}本题考查了点到线的最大值问题。圆中,到定弦距离最大的点一定在过圆心的直线上。
(2019 年广元 15.)如图,抛物线 过点(-1,0),(0,2),且顶点在第一象限,
设 ,则 的取值范围是.
第13题图第13题图
M
D
E
CD
E
C
B A AB
第14题图
C
B
O
A
P
F
P
C
B
O
A
2BD
8 4 3+
2 2 6 2
6 2+ ( )2
6 2+ 8 4 3+
6 3 3+
)0(2 ≠++= acbxaxy
cbaM ++= 24 M
{答案}-6<M<6
{解析}本题考查了二次函数 y=ax 2+bx+c 的图象和性质. 抛物线 过点(-1,0),
(0,2),可得 b=a+2;由图象可得 a<0;顶点在第一象限,可得 >0,得 a>-2,从而得 a 的取值范
围是-2<a<0。 =4a+2(a+2)+2=6a+6.所以 的取值范围是-6<M<6
{题型:4-解答题}三、解答题(共 75 分)要求写出必要的解答步骤或证明过程.
(2019 年广元 16.)(6 分)计算:
{解析}本题考查了绝对值、零指数、负指数、特殊值三角函数,负数的绝对值是它的相反数,任何非零
数的零次方都等于 1, ,an30°= .
{答案}解: 原式=2- +1-(-3)+3× =2- +1+4+ =7
(2019 年广元 17.)先化简: ,再从 1,2,3 中选取一个适当的数代入求值.
{解析}本题考查了分式的化简求值. 先化简分式,再代值计算,代值时注意不能取使分母为 0 的值.
)0(2 ≠++= acbxaxy
2
b
a
−
cbaM ++= 24 M
°+−−−+− − 30tan3)3
1()2019(23 10π
1p
pa a
− = 3
3
3 3
3 3 3
44
1)11
3( 2 +−
−⋅−−− xx
xxx
{答案}解:原式=
由于 x≠1,2,所以 x 只能取 3.
当 x=3 时,原式=-5.
(2019 年广元 18.)(6 分)如图,已知:在△ABC 中,∠BAC=90°,延长 BA 到点 D,使 AD= AB,
点 E,F 分别是边 BC,AC 的中点.求证:DF=BE.
{解析}本题考查了三角形中位线和全等三角形的判定。
{答案}证明:∵点 E,F 分别是边 BC,AC 的中点
∴EF= AB,EF∥AB,AF=FC,BE=EC
∵AD= AB,∴EF=AD
∵∠BAC=90°,EF∥AB
∴∠DAC=∠EFC=90°,
在△DAF 与△EFC 中
∵AF=FC,∠DAC=∠EFC,AD = EF
( )
( )( )
( )
( )
( )
( )
( )( )
( )
2
2
2
2
2
2
2
3 1( 1)1 2
3 1 1 1
1 2
3 1 1
1 2
4 1
1 2
2 2 1
1 2
2
2
xxx x
x x x
x x
x x
x x
x x
x x
x x x
x x
x
x
− − + − −
− + − −= − −
− − −= − −
− −= − −
− + − −= − −
+= −
2
1
1
2
2
1
∴△DAF≌△EFC ∴DF=EC
又∵BE=EC ∴DF= BE
(2019 年广元 19.)(8 分)如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的
开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,
B.瓶装矿泉水,C.碳酸饮料,D 非碳酸饮料。根据统计结果绘制如下两个统计图,根据统计图提供的信
息,解答下列问题:
(1)这个班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种只限一瓶,价格如下表),则该班同学每天用于饮品的
人均花费是多少元?
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的 5 名班委干部(其中有两位班长记为 A,B,
其余三位记为 C,D,E)中随机抽取 2 名班委干部作为良好习惯监督员,请用列表法或画树状图的方法
求出恰好抽到两位班长的概率。
{解析}本题考查了统计与概率的综合应用.(1)由 B 饮品的条形图中的人数与扇形图中的百分数可求得这
个班级总人数;(2)考查加权平均数;(3)这相当于不放回的两步试验概型,通过列表格或画树状图
即可求解.
{答案}解:(1)15÷30%=50
答:这个班级有 50 名同学.(补全条形统计图略)
(2) .
答: 该班同学每天用于饮品的人均花费是 2.2 元
(3)列表格如下:
15 2 20 3 5 4 2.250
× + × + × =
A B C D E
A (A,B) (A,C) (A,D) (A,E)
B (B,A) (B,C) (B,D) (B,E)
C (C,A) (C,B) (C,D) (C,E)
D (D,A) (D,B) (D,C) (D,E)
E (E,A) (E,B) (E,C) (E,D)
由表格知,共有 20 种等可能结果,其中抽到 A 和 B 的有 2 种结果,因此抽到两位班长的概率为
.
(2019 年广元 20.)(8 分)某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙
种水果的进价每千克少 4 元,且用 800 元购进甲种水果的数量与用 1000 元购进乙种水果的数量相同。
(2)求甲、乙两种水果的单价分别是多少元?
(3)该水果商根据该水果店平常的销售情况确定,购进两种水果共 200 千克,其中甲种水果的数量不超
过乙种水果数量的 3 倍,且购买资金不超过 3420 元,购回后,水果决定甲种水果的销售价定为每千克 20
元,乙种水果的销售价定为每千克 25 元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
{解析}本题考查了分式方程的应用,一元一次不等式组的应用,以及一次函数的应用。
{答案}解:(1)设乙种水果每千克的单价是 x 元,则甲种水果每千克的单价是(x-4)元
根据题意,得
解之,得 x=20
经检验,x=20 是原方程的解
当 x=20 时,x-4=20-4=16
答:甲、乙两种水果的单价分别是 16 元/千克,20 元/千克。
(2)设水果商购进乙种水果 m 千克,获得的利润为 w 元
解之,得 50≤m≤55
W=(20-16)(200-m)+(25-20)m 即 w=m+800
2 1
20 10
=
800 1000
4x x
=−
( )
200 3
16 200 20 3420
m m
m m
− ≤
− + ≤
∵1>0,∴w 随 m 的增大而增大
∵50≤m≤55∴当 m=55 时,w 有最大值,此时,200-m=200-55=145,w= 55+800=855
答:水果商应购进乙种水果 55 千克,购进甲种水果 145 千克,,才能获得最大利润,最大利润是 855 元。
(2019 年广元 21.)(8 分)如图,某海监船以 60 海里/时的速度从 A 处出发沿正西方向巡逻,一可疑船
只在 A 的西北方向的 C 处,海监船航行 1.5 小时到达 B 处时接到警报,需巡查此可疑船只,此时可疑船
只仍在 B 的北偏西 30°方向的 C 处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速 90 海
里/时的速度追击,在 D 处海监船追到可疑船只,D 在 B 的北偏西 60°方向(以下结果保留根号)
(2)求 B,C 两处之间的距离;
(3)求海监船追到可疑船只所用的时间。
{解析}本题考查了解直角三角形中的方位角问题。
{答案}解:(1)过点 C 作 CE⊥AB 于点 E,在 R△ACE 中,∠AEB=90°,∠A=45°,∴CE=AE
设 CE=x,则 AE=x,∵AB=60×1.5=90,∴BE=x-90
在 R△CBE 中,∠CEB=90°,∠CBE=180°-(90+30)°=60°,BE= x-90,CE=x,
∵ ∴ 解之,得 x=135+45
∴
答:B,C 两处之间的距离为( )海里
(2)过点 C 作 CF⊥BD 于点 F
由题可知,R△CFB 中,∠CFB=90°,∠CBD=30°,
∴FB=CBcos30°=( )× =
第21题图
E
F
D C
AB
tanCE CBEBE
= ∠ tan 60°90
x
x
=− 3
135 45 3= 90 90 3sin 60 3
2
CECB
+= = +
90 90 3+
= 90 90 3CB = +
90 90 3+ 3
2 45 3 270+
∵CD∥AB,∠DBE=180°-30°-(90+30)°=30°,∴∠CDB=∠DBE=30°,∴CD=CB
又∵CF⊥BD∴DB=2FB=2×( )=90 +540
(90 +540)÷90= +6
∴海监船追到可疑船只所用的时间为( +6)小时
(2019 年广元 22.)(10 分)如图,平面直角坐标系中,直线 AB 与 轴交于点 B(0,7),与反比例函
数 在第二象限内的图象相交于点 A(﹣1,α)。
(1)求直线 AB 的解析式;
(2)将直线 AB 向下平移 9 个单位后与反比例函数的图象交于点 C 和点 E,与 轴交于点 D,求△ACD
的面积;
(3)设直线 CD 的解析式为 ,根据图象直接写出不等式 的解集。
{解析}本题考查了反比例函数与一次函数的交点问题,三角形的面积求法,以及一次函数图象
与几何变换。
{答案}解:(1)∵反比例函数 的图象经过点 A(﹣1,α)∴α= =8∴A(﹣1,8)
设直线 AB 的解析式为 y=kx+b
∵直线 AB 经过点 B(0,7),A(﹣1,8)∴ 解之,得
∴直线 AB 的解析式为 y=-x+7
(2)根据题意得直线 DE 的表达式为 y=-x-2
45 3 270+ 3
3 3
3
y
xy 8−=
y
nmxy +=
xnmx 8−≤+
xy 8−= 8
1
−
−
7
8
b
k b
=
= − +
7
1
b
k
=
= −
由 得 ,
∵点 C 在第二象限,∴点 C 的坐标为(-4,2)
在 y=-x-2 中,令 x=0,得 y=-2,∴点 D 的坐标为(0,-2)
过点 A(﹣1,8)作 AF∥y 轴,交直线 DE 于点 F,则点 F 的坐标为(-1,-1)
∴AF=8-(-1)=9
∴S△ACD=
答:△ACD 的面积为 6.5
(3)不等式 的解集为-4≤x<0 或 x≥2
(2019 年广元 23. )(10 分)如图,AB 是⊙O 的直径,点 P 是 BA 延长线上一点,过点 P 作⊙O
的切线 PC,切点是 C,过点 C 作弦 CD AB 于点 E,连接 CO,CB。
(4)求证:PD 是⊙O 的切线;
(5)若 AB=10,anB= ,求 PA 的长;
(6)试探究线段 AB,OE,OP 之间的数量关系,并说明理由。
{解析}本题考查了圆的切线的判定,相似三角形的性质。
{答案}(1)证明:连接 OD
∵PC 切⊙O 于点 C,∴OC⊥PC∴∠OCP=90°
∵CO=DO,CD⊥OA∴∠COA=∠DOA
又∵CO=DO,OP=OP∴△OPC≌△OPD∴∠OCP=∠ODP=90°∴OD⊥PD
又∵OD 是⊙O 的半径,∴PD 是⊙O 的切线。
8
2
y x
y x
− =
= − −
1
1
4
2
x
y
= −
=
2
2
2
4
x
y
=
= −
1 1 9 0 ( 4) 6.52 2D CAF x x× − = × × − − =
xnmx 8−≤+
⊥
2
1
(2)设 CE=x∵CD⊥AB∴∠CEB=90°∵anB= ,∴BE=
∵AB=10,∴OB=OA=OC=5∴OE=2x-5
在 R△CEO 中∵∠CEB=90°∴CE2+OE2=OC2 即 x2+(2x-5)2=52
解之,得 x1=4,x2=0(舍去)∴OE=2x-5=2×4-5=3 在 R△CPO 中,∠OCP=90°
又∵CD AB∴OC2=OE▪OP52=3OP∴OP= ∴PA=OP-OA= -5=
(3)答:AB2=4OE▪OP,理由是∵OC2=OE▪OP∴( AB)2= OE▪OP∴AB2=4OE▪OP
(2019 年广元 24. )(12 分)如图,直线 与 轴, 轴分别交于 A,B 两点,过 A,B 两点
的抛物线 与 轴交于 C(-1,0)。
(4)求抛物线的解析式;
(5)连接 BC,若点 E 是线段 AC 上的一个动点(不与 A,C 重合),过点 E 作 EF//BC,交 AB 于点 F,
当△BEF 的面积是 时,求点 E 的坐标;
(6)在(2)的结论下,将△BEF 绕点 F 旋转 180°得△B´E´F´,试判断点 E´是否在抛物线上,并说明理
由。
{解析}本题考查了确定二次函数表达式,及点的坐标。
{答案}解:(1)在直线 中,令 x=0,得 y=4;令 y=0,得 x=4;所以点 A(4,0),B(0,4)
抛物线 过 A(4,0),B(0,4),C(-1,0)
2
1 21tan
2
CE x xB
= =
⊥ 25
3
25
3
10
3
1
2
4+−= xy x y
cbxaxy ++= 2 x
2
5
4+−= xy
cbxaxy ++= 2
∴ ,解之,得
∴抛物线的解析式为 y=-x2+3x+4
(2)设点 E(m,0),则 CE=m+1,AE+4-m
S△BCA= AC▪OB= ×5×4=10
S△BCE= CE▪OB= (m+1)×4=2(m+1)
∵EF∥BC
∴
∴
∴S△AEF=
∵S△BEF= S△ABC- S△BCE-S△AEF=
∴10-2(m+1)-( )=
解之,得 m1=m2=
∴点 E 的坐标为( ,0)
(3)答:E´不在抛物线上。理由是
∵点 F 在直线 上
∴设点 F(n,-n+4)
过点 F 作 FH⊥x 轴于点 H,则 EH=n- ,FH=-n+4
∵EF∥BC
0 16 4
4
0
a b c
c
a b c
= + +
=
= − +
1
3
4
a
b
c
= −
=
=
1
2
1
2
1
2
1
2
2
AEF
ACB
S AE
S AC
=
24
10 5
AEFS m− =
22 16 32
5 5 5m m− +
5
2
22 16 32
5 5 5m m− + 5
2
3
2
3
2
4+−= xy
3
2
∴∠BCO=∠FEH
∴an∠BCO=an∠FEH
∴
∴
解之,得 n=2,
∴F(2,2)
∵将△BEF 绕点 F 旋转 180°得△B´E´F´,E( ,0),F(2,2)
∴E’( ,4)
在 y=-x2+3x+4 中,当 x= 时,y=-( )2+3× +4= ≠4
∴E´不在抛物线上
BO FH
CO EH
=
4 4
31
2
n
n
− +=
−
3
2
5
2
5
2
5
2
5
2
21
4