2017年浙江省温州市中考数学试卷

2017年浙江省温州市中考数学试卷

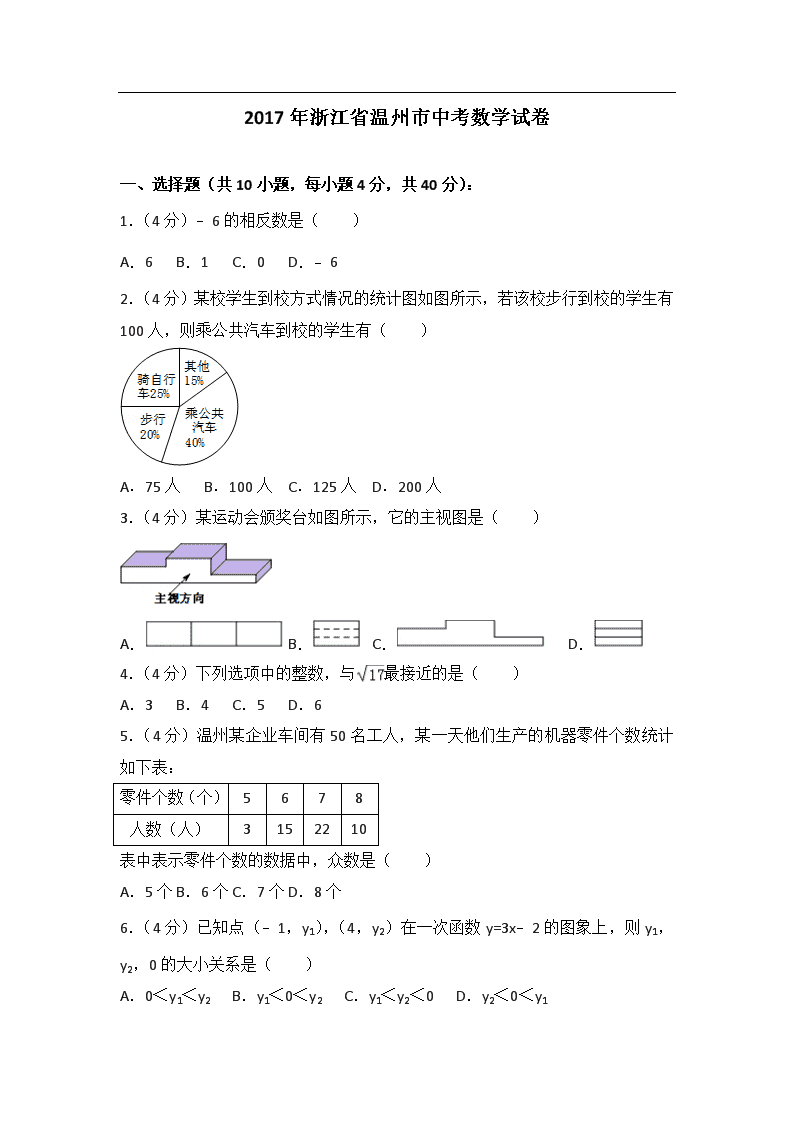
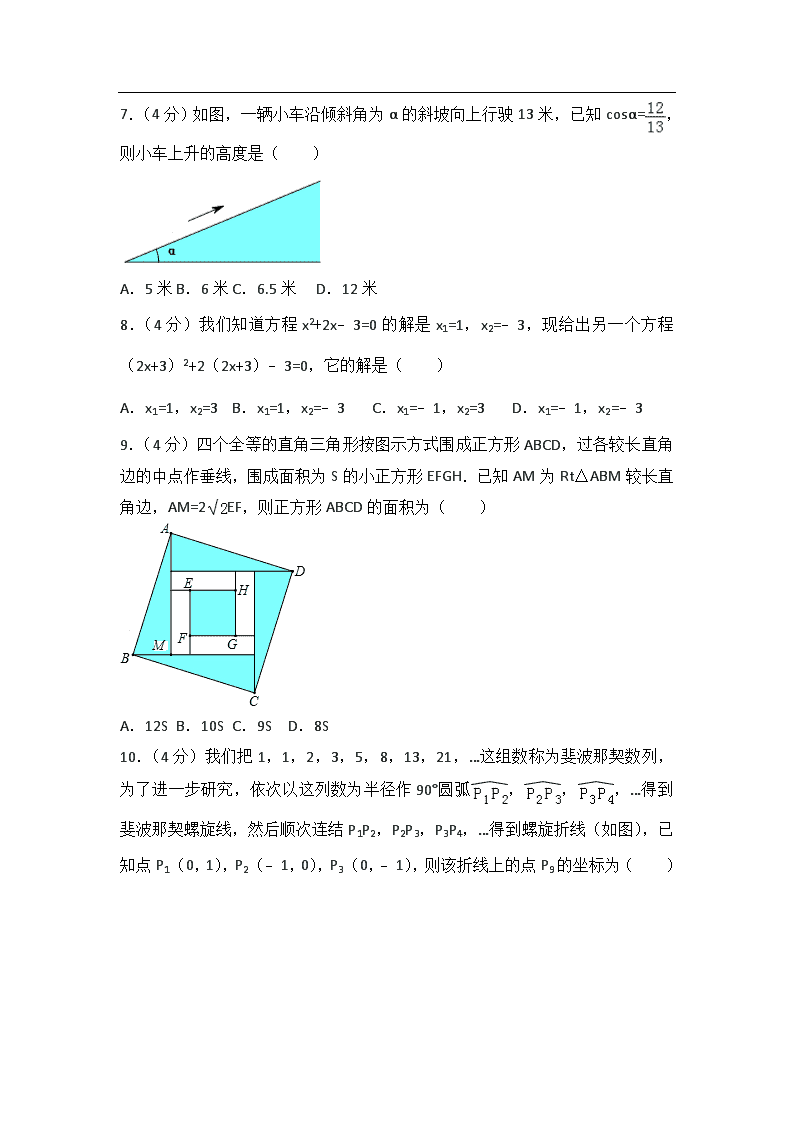
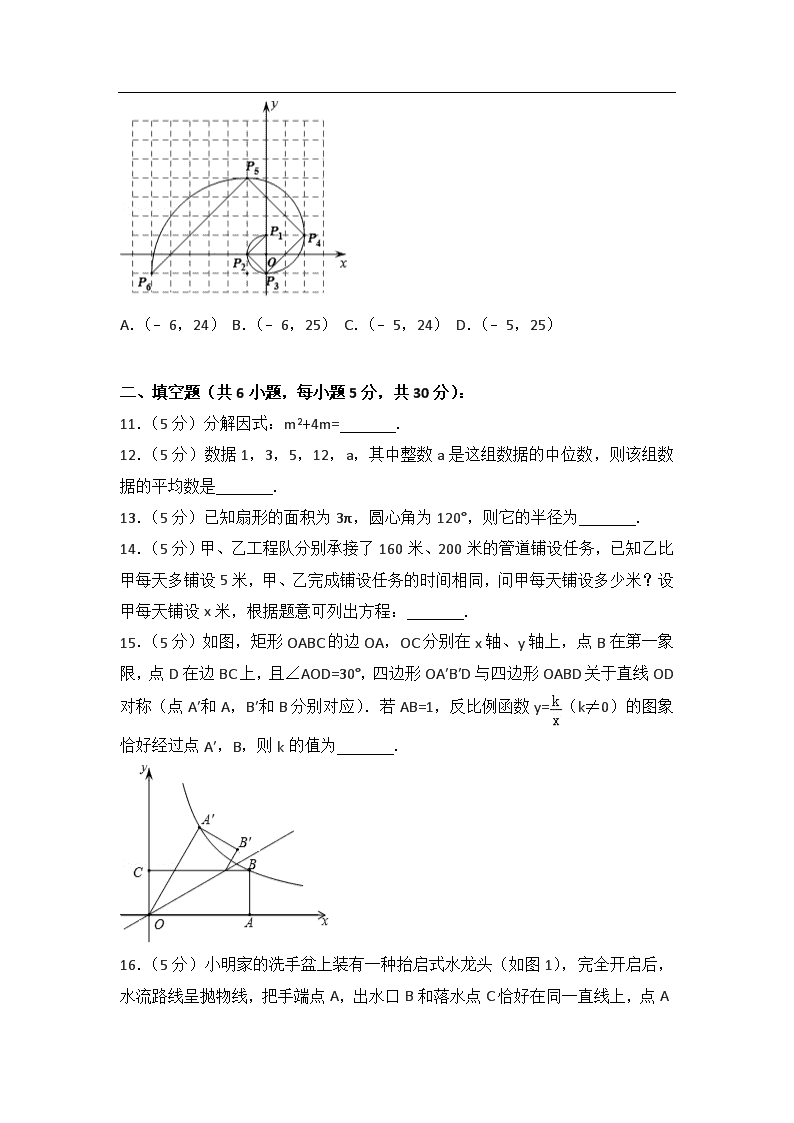
2017 年浙江省温州市中考数学试卷 　 一、选择题（共 10 小题，每小题 4 分，共 40 分）： 1．（4 分）﹣6 的相反数是（　　） A．6 B．1 C．0 D．﹣6 2．（4 分）某校学生到校方式情况的统计图如图所示，若该校步行到校的学生有 100 人，则乘公共汽车到校的学生有（　　） A．75 人 B．100 人 C．125 人 D．200 人 3．（4 分）某运动会颁奖台如图所示，它的主视图是（　　） A． B． C． D． 4．（4 分）下列选项中的整数，与 最接近的是（　　） A．3 B．4 C．5 D．6 5．（4 分）温州某企业车间有 50 名工人，某一天他们生产的机器零件个数统计 如下表： 零件个数（个） 5 6 7 8 人数（人） 3 15 22 10 表中表示零件个数的数据中，众数是（　　） A．5 个 B．6 个 C．7 个 D．8 个 6．（4 分）已知点（﹣1，y1），（4，y2）在一次函数 y=3x﹣2 的图象上，则 y1， y2，0 的大小关系是（　　） A．0＜y1＜y2 B．y1＜0＜y2 C．y1＜y2＜0 D．y2＜0＜y1 7．（4 分）如图，一辆小车沿倾斜角为 α 的斜坡向上行驶 13 米，已知 cosα= ， 则小车上升的高度是（　　） A．5 米 B．6 米 C．6.5 米 D．12 米 8．（4 分）我们知道方程 x2+2x﹣3=0 的解是 x1=1，x2=﹣3，现给出另一个方程 （2x+3）2+2（2x+3）﹣3=0，它的解是（　　） A．x1=1，x2=3 B．x1=1，x2=﹣3 C．x1=﹣1，x2=3 D．x1=﹣1，x2=﹣3 9．（4 分）四个全等的直角三角形按图示方式围成正方形 ABCD，过各较长直角 边的中点作垂线，围成面积为 S 的小正方形 EFGH．已知 AM 为 Rt△ABM 较长直 角边，AM=2 EF，则正方形 ABCD 的面积为（　　） A．12S B．10S C．9S D．8S 10．（4 分）我们把 1，1，2，3，5，8，13，21，…这组数称为斐波那契数列， 为了进一步研究，依次以这列数为半径作 90°圆弧 ， ， ，…得到 斐波那契螺旋线，然后顺次连结 P1P2，P2P3，P3P4，…得到螺旋折线（如图），已 知点 P1（0，1），P2（﹣1，0），P3（0，﹣1），则该折线上的点 P9 的坐标为（　　） A．（﹣6，24） B．（﹣6，25） C．（﹣5，24） D．（﹣5，25） 　 二、填空题（共 6 小题，每小题 5 分，共 30 分）： 11．（5 分）分解因式：m2+4m=　 　． 12．（5 分）数据 1，3，5，12，a，其中整数 a 是这组数据的中位数，则该组数 据的平均数是　 　． 13．（5 分）已知扇形的面积为 3π，圆心角为 120°，则它的半径为　 　． 14．（5 分）甲、乙工程队分别承接了 160 米、200 米的管道铺设任务，已知乙比 甲每天多铺设 5 米，甲、乙完成铺设任务的时间相同，问甲每天铺设多少米？设 甲每天铺设 x 米，根据题意可列出方程：　 　． 15．（5 分）如图，矩形 OABC 的边 OA，OC 分别在 x 轴、y 轴上，点 B 在第一象 限，点 D 在边 BC 上，且∠AOD=30°，四边形 OA′B′D 与四边形 OABD 关于直线 OD 对称（点 A′和 A，B′和 B 分别对应）．若 AB=1，反比例函数 y= （k≠0）的图象 恰好经过点 A′，B，则 k 的值为　 　． 16．（5 分）小明家的洗手盆上装有一种抬启式水龙头（如图 1），完全开启后， 水流路线呈抛物线，把手端点 A，出水口 B 和落水点 C 恰好在同一直线上，点 A 至出水管 BD 的距离为 12cm，洗手盆及水龙头的相关数据如图 2 所示，现用高 10.2cm 的圆柱型水杯去接水，若水流所在抛物线经过点 D 和杯子上底面中心 E， 则点 E 到洗手盆内侧的距离 EH 为　 　cm． 　 三、解答题（共 8 小题，共 80 分）： 17．（10 分）（1）计算：2×（﹣3）+（﹣1）2+ ； （2）化简：（1+a）（1﹣a）+a（a﹣2）． 18．（8 分）如图，在五边形 ABCDE 中，∠BCD=∠EDC=90°，BC=ED，AC=AD． （1）求证：△ABC≌△AED； （2）当∠B=140°时，求∠BAE 的度数． 19．（8 分）为培养学生数学学习兴趣，某校七年级准备开设“神奇魔方”、“魅力 数独”、“数学故事”、“趣题巧解”四门选修课（每位学生必须且只选其中一门）． （1）学校对七年级部分学生进行选课调查，得到如图所示的统计图．根据该统 计图，请估计该校七年级 480 名学生选“数学故事”的人数． （2）学校将选“数学故事”的学生分成人数相等的 A，B，C 三个班，小聪、小慧 都选择了“数学故事”，已知小聪不在 A 班，求他和小慧被分到同一个班的概 率．（要求列表或画树状图） 20．（8 分）在直角坐标系中，我们把横、纵坐标都为整数的点称为整点，记顶 点都是整点的三角形为整点三角形．如图，已知整点 A（2，3），B（4，4），请 在所给网格区域（含边界）上按要求画整点三角形． （1）在图 1 中画一个△PAB，使点 P 的横、纵坐标之和等于点 A 的横坐标； （2）在图 2 中画一个△PAB，使点 P，B 横坐标的平方和等于它们纵坐标和的 4 倍． 21．（10 分）如图，在△ABC 中，AC=BC，∠ACB=90°，⊙O（圆心 O 在△ABC 内 部）经过 B、C 两点，交 AB 于点 E，过点 E 作⊙O 的切线交 AC 于点 F．延长 CO 交 AB 于点 G，作 ED∥AC 交 CG 于点 D （1）求证：四边形 CDEF 是平行四边形； （2）若 BC=3，tan∠DEF=2，求 BG 的值． 22．（10 分）如图，过抛物线 y= x2﹣2x 上一点 A 作 x 轴的平行线，交抛物线于 另一点 B，交 y 轴于点 C，已知点 A 的横坐标为﹣2． （1）求抛物线的对称轴和点 B 的坐标； （2）在 AB 上任取一点 P，连结 OP，作点 C 关于直线 OP 的对称点 D； ①连结 BD，求 BD 的最小值； ②当点 D 落在抛物线的对称轴上，且在 x 轴上方时，求直线 PD 的函数表达 式． 23．（12 分）小黄准备给长 8m，宽 6m 的长方形客厅铺设瓷砖，现将其划分成 一个长方形 ABCD 区域Ⅰ（阴影部分）和一个环形区域Ⅱ（空白部分），其中区 域Ⅰ用甲、乙、丙三种瓷砖铺设，且满足 PQ∥AD，如图所示． （1）若区域Ⅰ的三种瓷砖均价为 300 元/m2，面积为 S（m2），区域Ⅱ的瓷砖均 价为 200 元/m2，且两区域的瓷砖总价为不超过 12000 元，求 S 的最大值； （2）若区域Ⅰ满足 AB：BC=2：3，区域Ⅱ四周宽度相等 ①求 AB，BC 的长； ②若甲、丙两瓷砖单价之和为 300 元/m2，乙、丙瓷砖单价之比为 5：3，且区域 Ⅰ的三种瓷砖总价为 4800 元，求丙瓷砖单价的取值范围． 24．（14 分）如图，已知线段 AB=2，MN⊥AB 于点 M，且 AM=BM，P 是射线 MN 上一动点，E，D 分别是 PA，PB 的中点，过点 A，M，D 的圆与 BP 的另一交点 C （点 C 在线段 BD 上），连结 AC，DE． （1）当∠APB=28°时，求∠B 和 的度数； （2）求证：AC=AB． （3）在点 P 的运动过程中 ①当 MP=4 时，取四边形 ACDE 一边的两端点和线段 MP 上一点 Q，若以这三点 为顶点的三角形是直角三角形，且 Q 为锐角顶点，求所有满足条件的 MQ 的值； ②记 AP 与圆的另一个交点为 F，将点 F 绕点 D 旋转 90°得到点 G，当点 G 恰好落 在 MN 上时，连结 AG，CG，DG，EG，直接写出△ACG 和△DEG 的面积之比． 　 2017 年浙江省温州市中考数学试卷 参考答案与试题解析 　 一、选择题（共 10 小题，每小题 4 分，共 40 分）： 1．（4 分）（2017•温州）﹣6 的相反数是（　　） A．6 B．1 C．0 D．﹣6 【分析】根据相反数的定义求解即可． 【解答】解：﹣6 的相反数是 6， 故选：A． 【点评】本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“﹣” 号：一个正数的相反数是负数，一个负数的相反数是正数，0 的相反数是 0．不 要把相反数的意义与倒数的意义混淆． 　 2．（4 分）（2017•温州）某校学生到校方式情况的统计图如图所示，若该校步行 到校的学生有 100 人，则乘公共汽车到校的学生有（　　） A．75 人 B．100 人 C．125 人 D．200 人 【分析】由扇形统计图可知，步行人数所占比例，再根据统计表中步行人数是 100 人，即可求出总人数以及乘公共汽车的人数； 【解答】解：所有学生人数为 100÷20%=500（人）； 所以乘公共汽车的学生人数为 500×40%=200（人）． 故选 D． 【点评】此题主要考查了扇形统计图的综合运用，读懂统计图，从不同的统计图 中得到必要的信息是解决问题的关键．扇形统计图直接反映部分占总体的百分比 大小． 　 3．（4 分）（2017•温州）某运动会颁奖台如图所示，它的主视图是（　　） A． B． C． D． 【分析】根据从正面看得到的图形是主视图，可得答案． 【解答】解：从正面看 ， 故选：C． 【点评】本题考查了简单组合体的三视图，从正面看得到的图形是主视图． 　 4．（4 分）（2017•温州）下列选项中的整数，与 最接近的是（　　） A．3 B．4 C．5 D．6 【分析】依据被开放数越大对应的算术平方根越大进行解答即可． 【解答】解：∵16＜17＜20.25， ∴4＜ ＜4.5， ∴与 最接近的是 4． 故选：B． 【点评】本题主要考查的是估算无理数的大小，掌握算术平方根的性质是解题的 关键． 　 5．（4 分）（2017•温州）温州某企业车间有 50 名工人，某一天他们生产的机器 零件个数统计如下表： 零件个数（个） 5 6 7 8 人数（人） 3 15 22 10 表中表示零件个数的数据中，众数是（　　） A．5 个 B．6 个 C．7 个 D．8 个 【分析】根据众数的定义，找数据中出现最多的数即可． 【解答】解：数字 7 出现了 22 次，为出现次数最多的数，故众数为 7 个， 故选 C． 【点评】本题考查了众数的概念．众数是数据中出现次数最多的数．众数不唯 一． 　 6．（4 分）（2017•温州）已知点（﹣1，y1），（4，y2）在一次函数 y=3x﹣2 的图 象上，则 y1，y2，0 的大小关系是（　　） A．0＜y1＜y2 B．y1＜0＜y2 C．y1＜y2＜0 D．y2＜0＜y1 【分析】根据点的横坐标利用一次函数图象上点的坐标特征，即可求出 y1、y2 的 值，将其与 0 比较大小后即可得出结论． 【解答】解：∵点（﹣1，y1），（4， ）在一次函数 y=3x﹣2 的图象上， ∴y1=﹣5，y2=10， ∵10＞0＞﹣5， ∴y1＜0＜y2． 故选 B． 【点评】本题考查了一次函数图象上点的坐标特征，根据点的横坐标利用一次函 数图象上点的坐标特征求出 y1、y2 的值是解题的关键． 　 7．（4 分）（2017•温州）如图，一辆小车沿倾斜角为 α 的斜坡向上行驶 13 米， 已知 cosα= ，则小车上升的高度是（　　） A．5 米 B．6 米 C．6.5 米 D．12 米 【分析】在 Rt△ABC 中，先求出 AB，再利用勾股定理求出 BC 即可． 【解答】解：如图 AC=13，作 CB⊥AB， ∵cosα= = ， ∴AB=12， ∴BC= =132﹣122=5， ∴小车上升的高度是 5m． 故选 A． 【点评】此题主要考查解直角三角形，锐角三角函数，勾股定理等知识，解题的 关键是学 会构造直角三角形解决问题，属于中考常考题型． 　 8．（4 分）（2017•温州）我们知道方程 x2+2x﹣3=0 的解是 x1=1，x2=﹣3，现给出 另一个方程（2x+3）2+2（2x+3）﹣3=0，它的解是（　　） A．x1=1，x2=3 B．x1=1，x2=﹣3 C．x1=﹣1，x2=3 D．x1=﹣1，x2=﹣3[来源:学&科&网 Z&X&X&K] 【分析】先把方程（2x+3）2+2（2x+3）﹣3=0 看作关于 2x+3 的一元二次方程， 利用题中的解得到 2x+3=1 或 2x+3=﹣3，然后解两个一元一次方程即可． 【解答】解：把方程（2x+3）2+2（2x+3）﹣3=0 看作关于 2x+3 的一元二次方程， 所以 2x+3=1 或 2x+3=﹣3， 所以 x1=﹣1，x2=﹣3． 故选 D． 【点评】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知 数的值是一元二次方程的解． 　 9．（4 分）（2017•温州）四个全等的直角三角形按图示方式围成正方形 ABCD， 过各较长直角边的中点作垂线，围成面积为 S 的小正方形 EFGH．已知 AM 为 Rt△ ABM 较长直角边，AM=2 EF，则正方形 ABCD 的面积为（　　） A．12S B．10S C．9S D．8S 【分析】设 AM=2a．BM=b．则正方形 ABCD 的面积=4a 2+b2，由题意可知 EF= （2a﹣b）﹣2（a﹣b）=2a﹣b﹣2a+2b=b，由此即可解决问题． 【解答】解：设 AM=2a．BM=b．则正方形 ABCD 的面积=4a2+b2 由题意可知 EF=（2a﹣b）﹣2（a﹣b）=2a﹣b﹣2a+2b=b， ∵AM=2 EF， ∴2a=2 b， ∴a= b，[来源:学科网 ZXXK] ∵正方形 EFGH 的面积为 S， ∴b 2=S， ∴正方形 ABCD 的面积=4a2+b2=9b2=9S， 故选 C． 【点评】本题考查正方形的性质、勾股定理、线段的垂直平分线的定义等知识， 解题的关键是灵活运用所学知识解决问题，属于中考选择题中的压轴题． 　 10．（4 分）（2017•温州）我们把 1，1，2，3，5，8，13，21，…这组数称为斐 波那契数列，为了进一步研究，依次以这列数为半径作 90°圆弧 ， ， ，…得到斐波那契螺旋线，然后顺次连结 P1P2，P2P3，P3P4，…得到螺旋折线 （如图），已知点 P1（0，1），P2（﹣1，0），P3（0，﹣1），则该折线上的点 P9 的坐标为（　　） A．（﹣6，24） B．（﹣6，25） C．（﹣5，24） D．（﹣5，25） 【分析】观察图象，推出 P9 的位置，即可解决问题． 【解答】解：由题意，P5 在 P2 的正上方，推出 P9 在 P6 的正上方，且到 P6 的距离 =21+5=26， 所以 P9 的坐标为（﹣6，25）， 故选 B． 【点评】本题考查规律型：点的坐标等知识，解题的关键是理解题意，确定 P9 的位置． 　 二、填空题（共 6 小题，每小题 5 分，共 30 分）： 11．（5 分）（2017•温州）分解因式：m2+4m=　m（m+4）　． 【分析】直接提提取公因式 m，进而分解因 式得出答案． 【解答】解：m2+4m=m（m+4）． 故答案为：m（m+4）． 【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关 键． 　 12．（5 分）（2017•温州）数据 1，3，5，12，a，其中整数 a 是这组数据的中位 数，则该组数据的平均数是　4.8 或 5 或 5.2　． 【分析】根据中位数的定义确定整数 a 的值，由平均数的定义即可得出答案． 【解答】解：∵数据 1，3，5，12，a 的中位数是整数 a， ∴a=3 或 a=4 或 a=5， 当 a=3 时，这组数据的平均数为 =4.8， 当 a=4 时，这组数据的平均数为 =5， 当 a=5 时，这组数据的平均数为 =5.2， 故答案为：4.8 或 5 或 5.2． 【点评】本题主要考查了中位数和平均数，解题的关键是根据中位数的定义确定 a 的值． 　 13．（5 分）（2017•温州）已知扇形的面积为 3π，圆心角为 120°，则它的半径为　 3　． 【分析】根据扇形的面积公式，可得答案． 【解答】解：设半径为 r，由题意，得 πr2× =3π， 解得 r=3， 故答案为：3． 【点评】本题考查了扇形面积公式，利用扇形面积公式是解题关键． 　 14．（5 分）（2 017•温州）甲、乙工程队分别承接了 160 米、200 米的管道铺设 任务，已知乙比甲每天多铺设 5 米，甲、乙完成铺设任务的时间相同，问甲每天 铺设多少米？设甲每天铺设 x 米，根据题意可列出方程：　 = 　． 【分析】设甲每天铺设 x 米，则乙每天铺设（x+5）米，根据铺设时间= 和甲、乙完成铺设任务的时间相同列出方程即可． 【解答】解：设甲工程队每天铺设 x 米，则乙工程队每天铺设（x+5）米，由题 意得： = ． 故答案是： = ． 【点评】此题主要考查了由实际问题抽象出分式方程，关键是正确理解题意，找 出题目中的等量关系，再列出方程． 　 15．（5 分）（2017•温州）如图，矩形 OABC 的边 OA，OC 分别在 x 轴、y 轴上， 点 B 在第一象限，点 D 在边 BC 上，且∠AOD=30°，四边形 OA′B′D 与四边形 OABD 关于直线 OD 对称（点 A′和 A，B′和 B 分别对应）．若 AB=1，反比例函数 y= （k ≠0）的图象恰好经过点 A′，B，则 k 的值为　 　． 【分析】设 B（m，1），得到 OA=BC=m，根据轴对称的性质得到 OA′=OA=m，∠ A′OD=∠AOD=30°，求得∠A′OA=60°，过 A′作 A′E⊥OA 于 E，解直角三角形得到 A′ （ m， m），列方程即可得到结论． 【解答】解：∵四边形 ABCO 是矩形，AB=1， ∴设 B（m，1）， ∴OA=BC=m， ∵四边形 OA′B′D 与四边形 OABD 关于直线 OD 对称， ∴OA′=OA=m，∠A′OD=∠AOD=30°， ∴∠A′OA=60°， 过 A′作 A′E⊥OA 于 E， ∴OE= m，A′E= m， ∴A′（ m， m）， ∵反比例函数 y= （k≠0）的图象恰好经过点 A′，B， ∴ m• m=m， ∴m= ， ∴k= ． 故答案为： ． 【点评】本题考查了反比例函数图象上点的坐标特征，矩形的性质，轴对称的性 质，解直角三角形，正确的作出辅助线是解题的关键． 　 16．（5 分）（2017•温州）小明家的洗手盆上装有一种抬启式水龙头（如图 1）， 完全开启后，水流路线呈抛物线，把手端点 A，出水口 B 和落水点 C 恰好在同一 直线上，点 A 至出水管 BD 的距离为 12cm，洗手盆及水龙头的相关数据如图 2 所示，现用高 10.2cm 的圆柱型水杯去接水，若水流所在抛物线经过点 D 和杯子 上底面中心 E，则点 E 到洗手盆内侧的距离 EH 为　24﹣8 　cm． 【分析】先建立直角坐标系，过 A 作 AG⊥OC 于 G，交 BD 于 Q，过 M 作 MP⊥AG 于 P，根据△ABQ∽△ACG，求得 C（20，0），再根据水流所在抛物线经过点 D （0，24）和 B（12，24），可设抛物线为 y=ax2+bx+24，把 C（20，0），B（12， 24）代入抛物线，可得抛物线为 y=﹣ x2+ x+24，最后根据点 E 的纵坐标为 10.2，得出点 E 的横坐标为 6+8 ，据此可得点 E 到洗手盆内侧的距离． 【解答】解：如图所示，建立直角坐标系，过 A 作 AG⊥OC 于 G，交 BD 于 Q， 过 M 作 MP⊥AG 于 P， 由题可得，AQ=12，PQ=MD=6，故 AP=6，AG=36， ∴Rt△APM 中，MP=8，故 DQ=8=OG， ∴BQ=12﹣8=4， 由 BQ∥CG 可得，△ABQ∽△ACG， ∴ = ，即 = ， ∴CG=12，OC=12+8=20， ∴C（20，0）， 又∵水流所在抛物线经过点 D（0，24）和 B（12，24）， ∴可设抛物线为 y=ax2+bx+24， 把 C（20，0），B（12，24）代入抛物线，可得 ，解得 ， ∴抛物线为 y=﹣ x2+ x+24， 又∵点 E 的纵坐标为 10.2， ∴令 y=10.2，则 10.2=﹣ x2+ x+24， 解得 x1=6+8 ，x2=6﹣8 （舍去）， ∴点 E 的横坐标为 6+8 ， 又∵ON=30， ∴EH=30﹣（6+8 ）=24﹣8 ． 故答案为：24﹣8 ． 【点评】本题以水龙头接水为载体，考查了二次函数的应用以及相似三角形的应 用，在运用数学知识解决问题过程中，关注核心内容，经历测量、运算、建模等 数学实践活动为主线的问题探究过程，突出考查数学的应用意识和解决问题的能 力，蕴含数学建模，引导学生关注生活，利用数学方法解决实际问题． 　 三、解答题（共 8 小题，共 80 分）： 17．（10 分）（2017•温州）（1）计算：2×（﹣3）+（﹣1）2+ ； （2）化简：（1+a）（1﹣a）+a（a﹣2）． 【分析】（1）原式先计算乘方运算，化简二次根式，再计算乘法运算，最后算加 减运算即可得到结果． （2）运用平方差公式即可解答． 【解答】解：（1）原式=﹣6+1+2 =﹣5+2 ； （2）原式=1﹣a2+a2﹣2a=1﹣2a． 【点评】本题考查了平方差公式，实数的运算以及单项式乘多项式．熟记实数运 算法则即可解题，属于基础题． 　 18．（8 分）（2017•温州）如图，在五边形 ABCDE 中，∠BCD=∠EDC=90°， BC=ED，AC=AD． （1）求证：△ABC≌△AED；[来源:学科网 ZXXK] （2）当∠B=140°时，求∠BAE 的度数． 【分析】（1）根据∠ACD=∠ADC，∠BCD=∠EDC=90°，可得∠ACB=∠ADE，进而 运用 SAS 即可判定全等三角形； （2）根据全等三角形对应角相等，运用五边形内角和，即可得到∠BAE 的度 数． 【解答】解：（1）∵AC=AD， ∴∠ACD=∠ADC， 又∵∠BCD=∠EDC=90°，[来源:学§科§网 Z§X§X§K] ∴∠ACB=∠ADE， 在△ABC 和△AED 中， ， ∴△ABC≌△AED（SAS）； （2）当∠B=140°时，∠E=140°， 又∵∠BCD=∠EDC=90°， ∴五边形 ABCDE 中，∠BAE=540°﹣140°×2﹣90°×2=80°． 【点评】本题主要考查了全等三角形的判定与性质的运用，解题时注意：两边及 其夹角对应相等的两个三角形全等． 　 19．（8 分）（2017•温州）为培养学生数学学习兴趣，某校七年级准备开设“神奇 魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课（每位学生必须且只选 其中一门）． （1）学校对七年级部分学生进行选课调查，得到如图所示的统计图．根据该统 计图，请估计该校七年级 480 名学生选“数学故事”的人数． （2）学校将选“数学故事”的学生分成人数相等的 A，B，C 三个班，小聪、小慧 都选择了“数学故事”，已知小聪不在 A 班，求他和小慧被分到同一个班的概 率．（要求列表或画树状图） 【分析】（1）利用样本估计总体，用 480 乘以样本中选“数学故事”的人数所占的 百分比即可估计该校七年级 480 名学生选“数学故事”的人数； （2）画树状图展示所有 6 种等可能的结果数，再找出他和小慧被分到同一个班 的结果数，然后根据概率公式求解． 【解答】解：（1）480× =90， 估计该校七年级 480 名学生选“数学故事”的人数为 90 人； （2）画树状图为：[来源:学科网 ZXXK] 共有 6 种等可能的结果数，其中他和小慧被分到同一个班的结果数为 2， 所以他和小慧被分到同一个班的概率= = ． 【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能 的结果 n，再从中选出符合事件 A 或 B 的结果数目 m，然后利用概率公式计算事 件 A 或事件 B 的概率． 　 20．（8 分）（2017•温州）在直角坐标系中，我们把横、纵坐标都为整数的点称 为整点，记顶点都是整点的三角形为整点三角形．如图，已知整点 A（2，3），B （4，4），请在所给网格区域（含边界）上按要求画整点三角形． （1）在图 1 中画一个△PAB，使点 P 的横、纵坐标之和等于点 A 的横坐标； （2）在图 2 中画一个△PAB，使点 P，B 横坐标的平方和等于它们纵坐标和的 4 倍． 【分析】（1）设 P（x，y），由题意 x+y=2，求出整数解即可解决问题； （2）设 P（x，y），由题意 x2+42=4（4+y），求出整数解即可解决问题； 【解答】解：（1）设 P（x，y），由题意 x+y=2， ∴P（2，0）或（1，1）或（0，2）不合题意舍弃， △PAB 如图所示． （2）设 P（x，y），由题意 x2+42=4（4+y）， 整数解为（2，1）或（0，0）等，△PAB 如图所示． 【点评】本题考查作图﹣应用与设计、二元方程的整数解问题等知识，解题的关 键是理解题意，学会用转化的思想思考问题，属于中考常考题型． 　 21．（10 分）（2017•温州）如图，在△ABC 中，AC=BC，∠ACB=90°，⊙O（圆心 O 在△ABC 内部）经过 B、C 两点，交 AB 于点 E，过点 E 作⊙O 的切线交 AC 于点 F．延长 CO 交 AB 于点 G，作 ED∥AC 交 CG 于点 D （1）求证：四边形 CDEF 是平行四边形； （2）若 BC=3，tan∠DEF=2，求 BG 的值． 【分析】（1）连接 CE，根据等腰直角三角形的性质得到∠B=45°，根据切线的性 质得到∠FEO=90°，得到 EF∥OD，于是得到结论； （2）过 G 作 GN⊥BC 于 N，得到△GMB 是等腰直角三角形，得到 MB=GM，根 据平行四边形的性质得到∠FCD=∠FED，根据余角的性质得到∠CGM=∠ACD，等 量代换得到∠CGM=∠DEF，根据三角函数的定义得到 CM=2GM，于是得到结 论． 【解答】解：（1）连接 CE， ∵在△ABC 中，AC=BC，∠ACB=90°， ∴∠B=45°， ∴∠COE=2∠B=90°， ∵EF 是⊙O 的切线， ∴∠FEO=90°， ∴EF∥OC， ∵DE∥CF， ∴四边形 CDEF 是平行四边形； （2）过 G 作 GN⊥BC 于 N， ∴△GMB 是等腰直角三角形， ∴MB=GM， ∵四边形 CDEF 是平行四边形， ∴∠FCD=∠FED， ∵∠ACD+∠GCB=∠GCB+∠CGM=90°， ∴∠CGM=∠ACD， ∴∠CGM=∠DEF， ∵tan∠DEF=2， ∴tan∠CGM= =2， ∴CM=2GM， ∴CM+BM=2GM+GM=3， ∴GM=1， ∴BG= GM= ． 【点评】本题考查了切线的性质，平行四边形的判定和性质，等腰直角三角形的 判定和性质，解直角三角形，正确的作出辅助线是解题的关键． 　 22．（10 分）（2017•温州）如图，过抛物线 y= x2﹣2x 上一点 A 作 x 轴的平行线， 交抛物线于另一点 B，交 y 轴于点 C，已知点 A 的横坐标为﹣2． （1）求抛物线的对称轴和点 B 的坐标； （2）在 AB 上任取一点 P，连结 OP，作点 C 关于直线 OP 的对称点 D； ①连结 BD，求 BD 的最小值； ②当点 D 落在抛物线的对称轴上，且在 x 轴上方时，求直线 PD 的函数表达 式． 【分析】（1）首先确定点 A 的坐标，利用对称轴公式求出对称轴，再根据对称性 可得点 B 坐标； （2）①由题意点 D 在以 O 为圆心 OC 为半径的圆上，推出当 O、D、B 共线时， BD 的最小值=OB﹣OD； ②当点 D 在对称轴上时，在 Rt△OD=OC=5，OE=4，可得 DE= = =3，求出 P、D 的坐标即可解决问题； 【解答】解：（1）由题意 A（﹣2，5），对称轴 x=﹣ =4， ∵A、B 关于对称轴对称， ∴B（10，5）． （2）①如图 1 中， 由题意点 D 在以 O 为圆心 OC 为半径的圆上， ∴当 O、D、B 共线时，BD 的最小值=OB﹣OD= ﹣5=5 ﹣5． ②如图 2 中， 图 2 当点 D 在对称轴上时，在 Rt△ODE 中，OD=OC=5，OE=4， ∴DE= = =3， ∴点 D 的坐标为（4，3）． 设 PC=PD=x，在 Rt△PDK 中，x2=（4﹣x）2+22， ∴x= ， ∴P（ ，5）， ∴直线 PD 的解析式为 y=﹣ x+ ． 【点评】本题考查抛物线与 X 轴的交点、待定系数法、最短问题、勾股定理等知 识，解题的关键是熟练掌握二次函数的性质，学会利用辅助圆解决最短问题，属 于中考常考题型． 　 23．（12 分）（2017•温州）小黄准备给长 8m，宽 6m 的长方形客厅铺设瓷砖， 现将其划分成一个长方形 ABCD 区域Ⅰ（阴影部分）和一个环形区域Ⅱ（空白部 分），其中区域Ⅰ用甲、乙、丙三种瓷砖铺设，且满足 PQ∥AD，如图所示． （1）若区域Ⅰ的三种瓷砖均价为 300 元/m2，面积为 S（m2），区域Ⅱ的瓷砖均 价为 200 元/m2，且两区域的瓷砖总价为不超过 12000 元，求 S 的最大值； （2）若区域Ⅰ满足 AB：BC=2：3，区域Ⅱ四周宽度相等 ①求 AB，BC 的长； ②若甲、丙两瓷砖单价之和为 300 元/m2，乙、丙瓷砖单价之比为 5：3，且区域 Ⅰ的三种瓷砖总价为 4800 元，求丙瓷砖单价的取值范围． 【分析】（1）根据题意可得 300S+（48﹣S）200≤12000，解不等式即可； （2）①设区域Ⅱ四周宽度为 a，则由题意（6﹣2a）：（8﹣2a）=2：3，解得 a=1，由此即可解决问题； ②设乙、丙瓷砖单价分别为 5x 元/m2 和 3x 元/m2，则甲的单价为（300﹣3x）元/m2， 由 PQ∥AD，可得甲的面积=矩形 ABCD 的面积的一半= 12，设乙的面积为 s，则 丙的面积为（12﹣s），由题意 12（300﹣3x）+5x•s+3x•（12﹣s）=4800，解得 s= ，由 0＜s＜12，可得 0＜ ＜12，解不等式即可； 【解答】解：（1）由题意 300S+（48﹣S）200≤12000， 解得 S≤24． ∴S 的最大值为 24． （2）①设区域Ⅱ四周宽度为 a，则由题意（6﹣2a）：（8﹣2a）=2：3，解得 a=1， ∴AB=6﹣2a=4，CB=8﹣2a=6． ②设乙、丙瓷砖单价分别为 5x 元/m2 和 3x 元/m2，则甲的单价为（300﹣3x）元/m2， ∵PQ∥AD， ∴甲的面积= 矩形 ABCD 的面积的一半=12 ，设乙的面积为 s ，则丙的面积为 （12﹣s）， 由题意 12（300﹣3x）+5x•s+3x•（12﹣s）=4800， 解得 s= ， ∵0＜s＜12， ∴0＜ ＜12，又∵300﹣3x＞0， 综上所述，50＜x＜100，150＜3x＜300， ∴丙瓷砖单价 3x 的范围为 150＜3x＜300 元/m2． 【点评】本题考查不等式的应用、矩形的性质等知识，解题的关键是理解题意， 学会构建方程或不等式解决实际问题，属于中考常考题型． 　 24．（14 分）（2017•温州）如图，已知线段 AB=2，MN⊥AB 于点 M，且 AM=BM，P 是射线 MN 上一动点，E，D 分别是 PA，PB 的中点，过点 A，M，D 的圆与 BP 的另一交点 C（点 C 在线段 BD 上），连结 AC，DE． （1）当∠APB=28°时，求∠B 和 的度数； （2）求证：AC=AB． （3）在点 P 的运动过程中 ①当 MP=4 时，取四边形 ACDE 一边的两端点和线段 MP 上一点 Q，若以这三点 为顶点的三角形是直角三角形，且 Q 为锐角顶点，求所有满足条件的 MQ 的值； ②记 AP 与圆的另一个交点为 F，将点 F 绕点 D 旋转 90°得到点 G，当点 G 恰 好 落在 MN 上时，连结 AG，CG，DG，EG，直接写出△ACG 和△DEG 的面积之 比． 【分析】（1）根据三角形 ABP 是等腰三角形，可得∠B 的度数，再连接 MD，根 据 MD 为△PAB 的中位线，可得∠MDB=∠APB=28°，进而得到 =2∠MDB=56°； （2）根据∠BAP=∠ACB，∠BAP=∠B，即可得到∠ACB=∠B，进而得出 AC=AB； （3）①记 MP 与圆的另一个交点为 R，根据 AM2+MR2=AR2=AC2+CR2，即可得到 PR= ，MR= ，再根据 Q 为直角三角形锐角顶点，分四种情况进行讨论：当∠ ACQ=90°时，当∠QCD=90°时，当∠QDC=90°时，当∠AEQ=90°时，即可求得 MQ 的值为 或 或 ； ②先判定△DEG 是等边三角形，再根据 GMD=∠GDM，得到 GM=GD=1，过 C 作 CH⊥AB 于 H，由∠BAC=30°可得 CH= AC=1=MG，即可得到 CG=MH= ﹣1，进 而得出 S△ACG= CG×CH= ，再根据 S△DEG= ，即可得到△ACG 和△DEG 的 面积之比． 【解答】解：（1）∵MN⊥AB，AM=BM， ∴PA=PB， ∴∠PAB=∠B， ∵∠APB=28°， ∴∠B=76°， 如图 1，连接 MD， ∵MD 为△PAB 的中位线， ∴MD∥AP， ∴∠MDB=∠APB=28°， ∴ =2∠MDB=56°； （2）∵∠BAC=∠MDC=∠APB， 又∵∠BAP=180°﹣∠APB﹣∠B，∠ACB=180°﹣∠BAC﹣∠B， ∴∠BAP=∠ACB， ∵∠BAP=∠B， ∴∠ACB=∠B， ∴AC=AB； （3）①如图 2，记 MP 与圆的另一个交点为 R， ∵MD 是 Rt△MBP 的中线， ∴DM=DP， ∴∠DPM=∠DMP=∠RCD， ∴RC=RP， ∵∠ACR=∠AMR=90°， ∴AM2+MR2=AR2=AC2+CR2， ∴12+MR2=22+PR2， ∴12+（4﹣PR）2=22+PR2， ∴PR= ， ∴MR= ， Ⅰ．当∠ACQ=90°时，AQ 为圆的直径， ∴Q 与 R 重合， ∴MQ=MR= ； Ⅱ．如图 3，当∠QCD=90°时， 在 Rt△QCP 中，PQ=2PR= ， ∴MQ= ； Ⅲ．如图 4，当∠QDC=90°时， ∵BM=1，MP=4， ∴BP= ， ∴DP= BP= ， ∵cos∠MPB= = ， ∴PQ= ， ∴MQ= ； Ⅳ．如图 5，当∠AEQ=90°时， 由对称性可得∠AEQ=∠BDQ=90°， ∴MQ= ； 综上所述，MQ 的值为 或 或 ； ②△ACG 和△DEG 的面积之比为 ． 理由：如图 6，∵DM∥AF， ∴DF=AM=DE=1， 又由对称性可得 GE=GD， ∴△DEG 是等边三角形， ∴∠EDF=90°﹣60°=30°， ∴∠DEF=75°=∠MDE， ∴∠GDM=75°﹣60°=15°， ∴∠GMD=∠PGD﹣∠GDM=15°， ∴GMD=∠GDM， ∴GM=GD=1， 过 C 作 CH⊥AB 于 H， 由∠BAC=30°可得 CH= AC= AB=1=MG，AH= ， ∴CG=MH= ﹣1， ∴S△ACG= CG×CH= ， ∵S△DEG= ， ∴S△ACG：S△DEG= ． 【点评】本题属于圆的综合题，主要考查了等腰三角形的性质，等边三角形的判 定与性质，三角形中位线定理，勾股定理，圆周角定理以及解直角三角形的综合 应用，解决问题的关键是作辅助线构造直角三角形以及等边三角形，运用旋转的 性质以及含 30°角的直角三角形的性质进行计算求解，解题时注意分类思想的运 用．