二次函数　　教案1

二次函数　　教案1

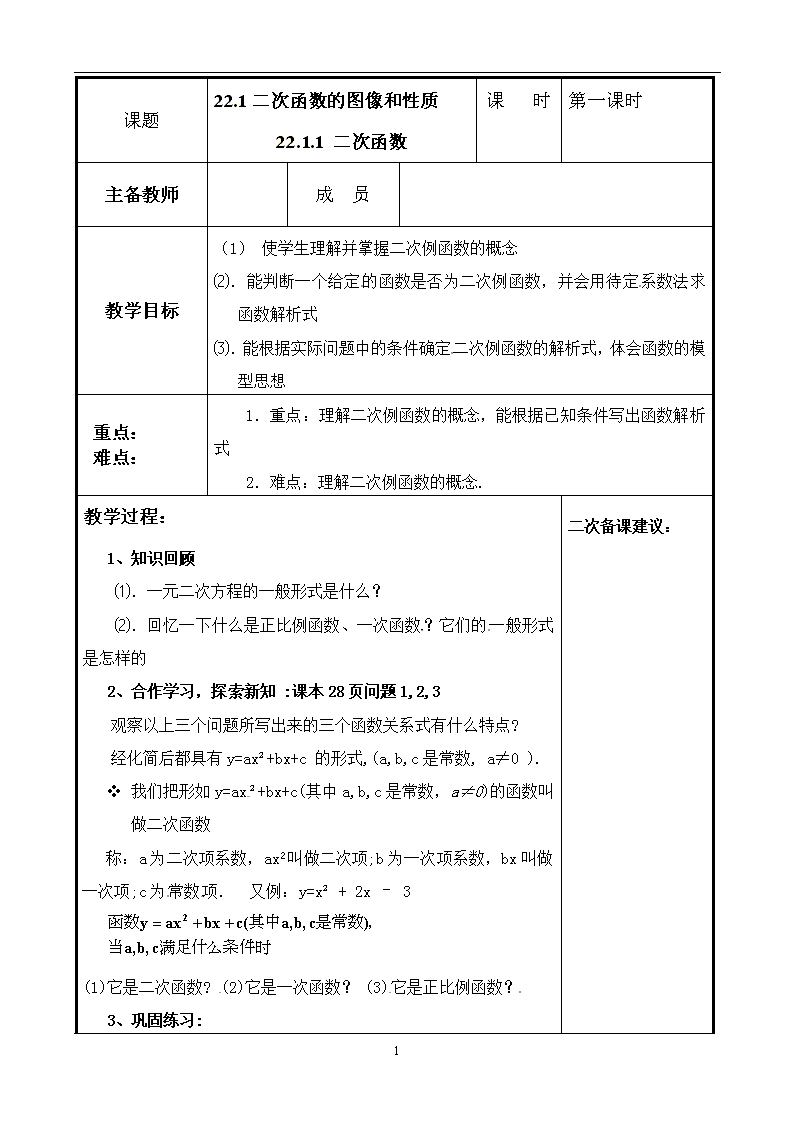
课题 ‎22.1二次函数的图像和性质 ‎22.1.1 二次函数 课 时 第一课时 主备教师 成 员 教学目标 （1） 使学生理解并掌握二次例函数的概念 ‎⑵．能判断一个给定的函数是否为二次例函数，并会用待定系数法求函数解析式 ‎⑶．能根据实际问题中的条件确定二次例函数的解析式，体会函数的模型思想 重点：‎ 难点：‎ ‎1．重点：理解二次例函数的概念，能根据已知条件写出函数解析式 ‎2．难点：理解二次例函数的概念.‎ 教学过程：‎ ‎1、知识回顾 ‎⑴．一元二次方程的一般形式是什么？‎ ‎⑵．回忆一下什么是正比例函数、一次函数？它们的一般形式是怎样的 ‎2、合作学习，探索新知 :课本28页问题1,2,3‎ 观察以上三个问题所写出来的三个函数关系式有什么特点?‎ 经化简后都具有y=ax²+bx+c 的形式,(a,b,c是常数, a≠0 ).‎ v 我们把形如y=ax²+bx+c(其中a,b, c是常数，a≠0)的函数叫做二次函数[来源:Zxxk.Com]‎ 称：a为二次项系数，ax2叫做二次项;b为一次项系数，bx叫做一次项;c为常数项. 又例：y=x² + 2x – 3‎ ‎ ‎ ‎(1)它是二次函数? (2)它是一次函数？ (3)它是正比例函数？‎ ‎3、巩固练习:‎ 二次备课建议：‎ 2‎ ‎ 1.下列函数中,哪些是二次函数?(1)y=3x-1 ; (2)y=3x2+2; (3)y=3x3+2x2; (4)y=2x2-2x+1; (5)y=x2-x(1+x); (6)y=x-2+x.‎ ‎ 2.做一做:课本29页 练习 ‎4、例题讲解:‎ 例1: 关于x的函数是二次函数, 求m的值. ‎ 注意:二次函数的二次项系数不能为零 例2:已知关于x的二次函数,当x=－1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式.(待定系数法)‎ 四、随堂练习:‎ ‎1、P6练习1，2;‎ ‎2、若函数 为二次函数，求m的值。‎ ‎3、已知二次函数y=x²+px+q,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的解析式 五、课堂小结:‎ 六、作业设置：1、 课本P16,1、2、课本P17、2 ‎ 板书设计 教学反思：‎ 2‎