2020九年级数学上册 第四次质量评估试卷 （新版）浙教版

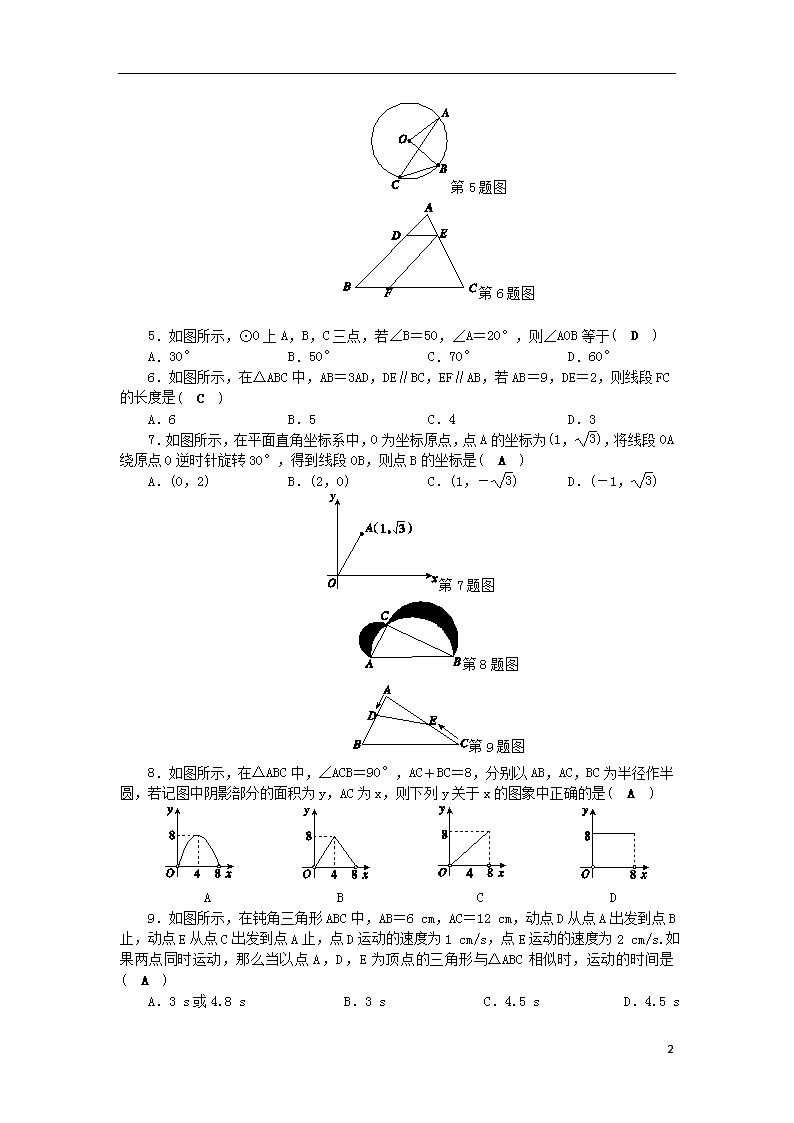
2020九年级数学上册 第四次质量评估试卷 （新版）浙教版

第四次质量评估试卷 ‎[考查范围：1～4章]‎ 一、选择题(每小题3分，共30分)‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ 第1题图 ‎1．如图所示，在△ABC中，DE∥BC，若AD∶DB＝2∶3，则下列结论中正确的是(　B　)‎ A.＝ B.＝ C.＝ D.＝ ‎2．若△ABC∽△DEF，它们的面积比为4∶1，则△ABC与△DEF的相似比为(　A　)‎ A．2∶1 B．1∶‎2 ‎ C．4∶1 D．1∶4‎ ‎3．在四张背面完全相同的卡片上分别印着等腰三角形、平行四边形、菱形、圆的图案，现将印有图案的一面朝下，混合后从中随机抽取两张，则抽到卡片上印有图案都是轴对称图形的概率为(　D　)‎ A. B. C. D. ‎4．如图所示，有三个矩形，其中互为相似图形的是(　B　)‎ A．甲和乙 B．甲和丙 C．乙和丙 D．甲、乙和丙 第4题图 9‎ ‎　　　　第5题图 ‎　　　　第6题图 ‎5．如图所示，⊙O上A，B，C三点，若∠B＝50，∠A＝20°，则∠AOB等于(　D　)‎ A．30° B．50° C．70° D．60°‎ ‎6．如图所示，在△ABC中，AB＝3AD，DE∥BC，EF∥AB，若AB＝9，DE＝2，则线段FC的长度是(　C　)‎ A．6 B．‎5 ‎ C．4 D．3‎ ‎7．如图所示，在平面直角坐标系中，O为坐标原点，点A的坐标为(1，)，将线段OA绕原点O逆时针旋转30°，得到线段OB，则点B的坐标是(　A　)‎ A．(0，2) B．(2，0) C．(1，－) D．(－1，)‎ 第7题图 ‎　　　　第8题图 ‎　　　　第9题图 ‎8．如图所示，在△ABC中，∠ACB＝90°，AC＋BC＝8，分别以AB，AC，BC为半径作半圆，若记图中阴影部分的面积为y，AC为x，则下列y关于x的图象中正确的是(　A　)‎ A　　　　　　　　　B　　　　　　　　　 C　　　　　　　　　D ‎9．如图所示，在钝角三角形ABC中，AB＝‎6 cm，AC＝‎12 cm，动点D从点A出发到点B止，动点E从点C出发到点A止，点D运动的速度为‎1 cm/s，点E运动的速度为‎2 cm/s.如果两点同时运动，那么当以点A，D，E为顶点的三角形与△ABC相似时，运动的时间是(　A　)‎ A．3 s或4.8 s B．3 s C．4.5 s D．4.5 s 9‎ 或4.8 s ‎10．抛物线y＝ax2＋bx＋3(a≠0)过A(4，4)，B(2，m)两点，点B到抛物线对称轴的距离记为d，满足0＜d≤1，则实数m的取值范围是(　B　)‎ A．m≤2或m≥3 B．m≤3或m≥4 ‎ C．2＜m＜3 D．3＜m＜4‎ 二、填空题(每小题4分，共24分)‎ ‎11．已知＝，则＝____．‎ ‎12．如图，∠DAB＝∠CAE，请你再补充一个边条件，使得△ABC∽△ADE：__∠D＝∠B(答案不唯一)__．‎ ‎13．圆内接四边形ABCD，两组对边的延长线分别相交于点E，F，且∠E＝40°，∠F＝60°，则∠A＝__40°__．‎ ‎　　第12题图 ‎　　　　第13题图 ‎　　　　第15题图 ‎　　　第16题图 ‎14．抛物线y＝x2＋bx＋c与x轴相交于A(－1，0)，B(3，0)两点，写出y＞－3时x的取值范围：__x＜0或x＞2__．‎ ‎15．如图所示，AD是△ABC的高，AE是△ABC的外接圆⊙O的直径，且AB＝4，AC＝5，AD＝4，则⊙O的直径AE＝__5__．‎ ‎16．如图所示，在Rt△ABC中，∠C＝90°，AC＝10，BC＝30，动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动，动点Q从点C开始沿边CA向点A以每秒1个单位长度的速度运动，连结PQ，点P，Q分别从点B，C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒(t≥0)．‎ ‎(1)当t＝__6__秒时，点P，C，Q所构成的三角形与Rt△ABC相似；‎ ‎(2)在整个运动过程中，线段PQ的中点所经过的路程长为__5__．‎ 三、解答题(共66分)‎ ‎17．(6分)有A，B，C三种款式的帽子，E，F两种款式的围巾，穿戴时小婷任意选一顶帽子和一条围巾．‎ 9‎ ‎(1)用合适的方法表示搭配的所有可能的结果；‎ ‎(2)求小婷恰好选中她所喜欢的A款帽子和E款围巾的概率．‎ 解：(1)根据题意，小婷任意选取一顶帽子和一条围巾，有A、E，A、F，B、E，B、F，C、E，C、F，6种情况，‎ ‎(2)小婷恰好选中她所喜欢的A款帽子和E款围巾的概率＝.‎ 第18题图 ‎18．(8分)“今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图所示，矩形ABCD，东边城墙AB长9里，南边城墙AD长7里，东门点E、南门点F分别是AB，AD的中点，EG⊥AB，FH⊥AD，EG＝15里，HG经过A点，求FH的长．‎ 解：∵EG⊥AB，FH⊥AD，HG经过A点，∴FA∥EG，EA∥FH，‎ ‎∴∠HFA＝∠AEG＝90°，∠FHA＝∠EAG，∴△AFH∽△GEA，∴＝.‎ ‎∵AB＝9里，AD＝7里，EG＝15里，∴FA＝3.5里，EA＝4.5里，∴＝，解得FH＝1.05里．‎ 第19题图 ‎19．(8分)如图所示，正方形ABCD的边长为1，其中弧DE、弧EF、弧FG的圆心依次为点A，B，C.‎ ‎(1)求点D沿三条弧运动到点G所经过的路线长；‎ ‎(2)判断直线GB与DF的位置关系，并说明理由．‎ 解：(1)根据弧长公式，得所求路线长为＋＋＝3π.‎ ‎(2)GB⊥DF.理由如下：‎ 在△FCD和△GCB中，∵ ‎∴△FCD≌△GCB(SAS)，∴∠G＝∠F，∵∠F＋∠FDC＝90°，∴∠G＋∠FDC＝90°，∴∠GHD＝90°，∴GB⊥DF.‎ 9‎ 第20题图 ‎20．(8分)如图所示，在矩形ABCD中，BE⊥AC分别交AC，AD于点F，E，若AD＝1，AB＝CF，求AE的长．‎ 解：∵四边形ABCD是矩形，∴BC＝AD＝1，∠BAE＝∠ABC＝90°，∴∠ABE＋∠CBF＝90°，‎ ‎∵BE⊥AC，∴∠BFC＝90°，∴∠BCF＋∠CBF＝90°，∴∠ABE＝∠FCB，‎ 在△ABE和△FCB中， ‎∴△ABE≌△FCB，∴BF＝AE，BE＝BC＝1，∵BE⊥AC，∴∠BAF＋∠ABF＝90°，‎ ‎∵∠ABF＋∠AEB＝90°，∴∠BAF＝∠AEB，∵∠BAE＝∠AFB，∴△ABE∽△FBA，∴＝，∴＝，∴AE＝AB2，‎ 在Rt△ABE中，BE＝1，根据勾股定理，得AB2＋AE2＝BE2＝1，∴AE＋AE2＝1，∵AE＞0，∴AE＝.‎ ‎21．(8分)已知一次函数y1＝x＋b 的图象与二次函数y2＝a(x2＋bx＋3)(a≠0，a，b 为常数)的图象交于A，B两点，且点A 的坐标为(0，3)．‎ ‎(1)求出a，b 的值；‎ ‎(2)求出点B 的坐标，并直接写出当y1≥y2时x 的取值范围；‎ ‎(3)设s＝y1＋y2，t＝y1－y2，若n≤x≤m 时，s 随着x 的增大而增大，且t 也随着x 的增大而增大，求n 的最小值和m 的最大值．‎ 解：(1)把A(0，3)代入y1＝x＋b中，得b＝3，∴y1＝x＋3，y2＝a(x2＋3x＋3)，把A(0，3)代入y2＝a(x2＋3x＋3)中，得3a＝3，a＝1，‎ ‎∴a＝1，b＝3.‎ ‎(2)由题意，得 解得或 第21题答图 ‎∴B(－2，1)，‎ 如图所示，当y1≥y2时x 的取值范围是－2≤x≤0.‎ ‎(3)s＝y1＋y2＝x＋3＋x2＋3x＋3＝x2＋4x＋6＝(x＋2)2＋2，∵抛物线开口向上，‎ 9‎ ‎∴当x≥－2时，s 随着x 的增大而增大，t＝y1－y2＝x＋3－(x2＋3x＋3)＝－x2－2x＝－(x＋1)2＋1，‎ ‎∵抛物线开口向下，∴当x≤－1时，t随着x 的增大而增大，‎ ‎∴当－2≤x≤－1时，s 随着x 的增大而增大，且t 也随着x 的增大而增大，‎ ‎∵n≤x≤m，s 随着x 的增大而增大，且t 也随着x 的增大而增大，‎ ‎∴n 的最小值－2，m 的最大值－1.‎ 第22题图 ‎22．(8分)有一块锐角三角形卡纸余料ABC，它的边BC＝‎120 cm，高AD＝‎80 cm，为使卡纸余料得到充分利用，现把它裁剪成一个邻边之比为2∶5的矩形纸片EFGH和正方形纸片PMNQ，裁剪时，矩形纸片的较长边在BC上，正方形纸片一边在矩形纸片的较长边EH上，其余顶点均分别在AB，AC上，具体裁剪方式如图所示．‎ ‎(1)求矩形纸片较长边EH的长；‎ ‎(2)裁剪正方形纸片时，小聪同学是按以下方法进行裁剪的：先沿着剩余料△AEH中与边EH平行的中位线剪一刀，再沿过该中位线两端点向边EH所作的垂线剪两刀，请你通过计算，判断小聪的剪法是否正确．‎ 解：(1)设EF＝2x，EH＝5x，∵矩形对边EH∥BC，∴△AEH∽△ABC，∴＝，即＝，解得x＝15，EH＝5x＝15×5＝75 cm，‎ 所以矩形纸片较长边EH的长为75 cm.‎ ‎(2)小聪的剪法不正确．‎ 理由如下：设正方形的边长为a，AR＝AD－RD＝80－2×15＝50 cm，AK＝50－a，由题意，知△APQ∽△AEH，‎ ‎∴＝，即＝，解得a＝30，与边EH平行的中位线＝×75＝37.5 cm，∵37.5≠30，∴小聪的剪法不正确．‎ 图(a)　　　　　　　　　图(b)‎ 第23题图 ‎23．(10分)(1)如图(a)所示，已知∠ACB＝∠DCE＝90°，AC＝BC＝6，CD＝CE，AE＝3，∠CAE＝45°，求AD的长；‎ 9‎ ‎(2)如图(b)所示，已知∠ACB＝∠DCE＝90°，∠ABC＝∠CED＝∠CAE＝30°，AC＝3，AE＝8，求AD的长．‎ 解：(1)如图(a)所示，连结BE，∵∠ACB＝∠DCE＝90°，‎ ‎∴∠ACB＋∠ACE＝∠DCE＋∠ACE，即∠BCE＝∠ACD，‎ 又∵AC＝BC，DC＝EC，在△ACD和△BCE中， ‎∴△ACD≌△BCE，∴AD＝BE，∵AC＝BC＝6，∴AB＝6，∵∠ACB＝90°，AC＝BC，∴∠BAC＝∠ABC＝45°.‎ ‎∵∠BAC＝∠CAE＝45°，∴∠BAE＝90°，在Rt△BAE中，AB＝6，AE＝3，∴BE＝9，∴AD＝9.‎ 第23题答图(a)‎ ‎　　　第23题答图(b)‎ ‎(2)如图(b)所示，连结BE，∵∠ACB＝∠DCE＝90°，∠ABC＝∠CED＝30°，∴＝＝，AB＝‎2AC＝6，∠BAC＝60°.‎ ‎∵∠ACB＝∠DCE＝90°，∠ABC＝∠CED＝30°，∴Rt△ABC∽Rt△DCE，∴＝，∴∠BCE＝∠ACD，‎ ‎∴△ACD∽△BCE，∴＝＝，∵∠BAC＝60°，∠CAE＝30°，∴∠BAE＝90°，又AB＝6，AE＝8，∴BE＝10，∴AD＝ .‎ ‎24．(10分)在平面直角坐标系中，抛物线y＝－x2＋x＋4的图象与x轴交于B，C两点(B在C的左侧)，与y轴交于点A.‎ ‎(1)求出点A，B，C的坐标；‎ ‎(2)在抛物线上有一动点P，抛物线的对称轴上有另一动点Q，若以B，C，P，Q为顶点的四边形是平行四边形，直接写出点P的坐标；‎ ‎(3)向右平移抛物线，使平移后的抛物线恰好经过△ABC的外心，求出平移后的抛物线的解析式．‎ 解：(1)当x＝0时，y＝4，∴与y轴交点A(0，4)，当y＝0时，－x2＋x＋4＝0，‎ 9‎ 解得：x1＝－2，x2＝8，∴B(－2，0)，C(8，0)．‎ ‎(2)y＝－x2＋x＋4＝－(x－3)2＋，当P在x轴的上方时，即为抛物线的顶点P时，可以构成平行四边形BPCQ，如图1，‎ 当P在x轴的下方时，∵BC＝2＋8＝10，若四边形BPCQ为平行四边形，则BC∥PQ，BC＝PQ＝10，‎ 有两种情况：①当P在抛物线对称轴的左侧时，如图2，‎ ‎∴点P的横坐标为－7，当x＝－7时，y＝－×(－7)2＋×(－7)＋4＝－，此时P；‎ ‎②当P在抛物线对称轴的右侧时，如图3，‎ ‎∴点P的横坐标为13，当x＝13时，y＝－×132＋×13＋4＝－，此时P；‎ 综上所述，点P的坐标为P或或.‎ ‎(3)如图3，‎ ‎∵A(0，4)，B(－2，0)，C(8，0)，∴OA＝4，OB＝2，OC＝8，∴＝＝，＝＝，∴＝，‎ ‎∵∠AOB＝∠AOC＝90°，∴△AOB∽△COA，∴∠BAO＝∠ACO，‎ ‎∵∠ACO＋∠OAC＝90°，∴∠BAO＋∠OAC＝90°，∴∠BAC＝90°，‎ ‎∴△ABC是直角三角形，∴△ABC的外心就是斜边AB的中点E，‎ ‎∵BC＝10，∴BC的中点E的坐标为(3，0)，‎ 即平移后的解析式经过E(3，0)，‎ ‎∴相当于把原抛物线向右平移5个单位，‎ ‎∴平移后的解析式为y＝－(x－3－5)2＋＝－x2＋4x－.‎ 第24题答图 9‎ ‎　　　　第24题答图 ‎　　　　第24题答图 9‎