北京市2008-2019年中考数学分类汇编探究性试题之代数篇pdf含解析

北京市2008-2019年中考数学分类汇编探究性试题之代数篇pdf含解析

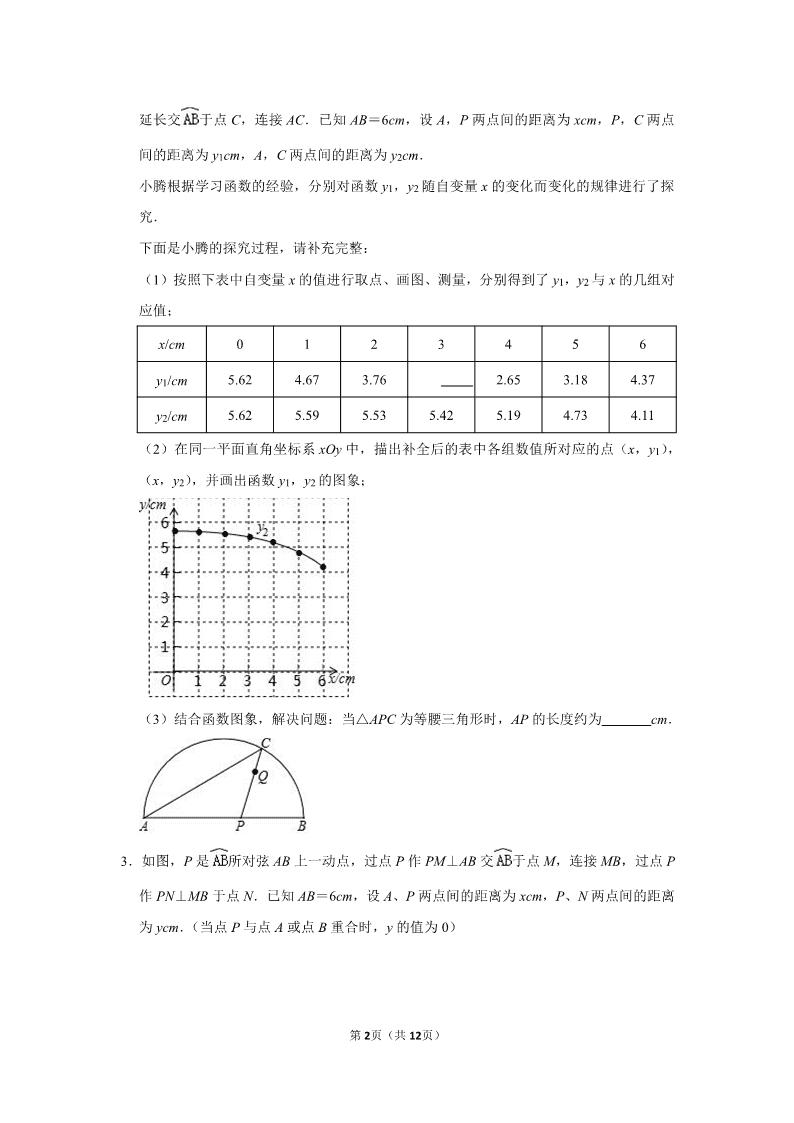
第 1页（共 12页） 2008～2019 北京中考数学分类汇编(探究性试题之代数篇) 一．解答题（共 5 小题） 1．如图，P 是 与弦 AB 所围成的图形的外部的一定点，C 是 上一动点，连接 PC 交弦 AB 于点 D． 小腾根据学习函数的经验，对线段 PC，PD，AD 的长度之间的关系进行了探究．下面是 小腾的探究过程，请补充完整： （1）对于点 C 在 上的不同位置，画图、测量，得到了线段 PC，PD，AD 的长度的几 组值，如下表： 位置 1 位置 2 位置 3 位置 4 位置 5 位置 6 位置 7 位置 8 PC/cm 3.44 3.30 3.07 2.70 2.25 2.25 2.64 2.83 PD/cm 3.44 2.69 2.00 1.36 0.96 1.13 2.00 2.83 AD/cm 0.00 0.78 1.54 2.30 3.01 4.00 5.11 6.00 在 PC，PD，AD 的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数； （2）在同一平面直角坐标系 xOy 中，画出（1）中所确定的函数的图象； （3）结合函数图象，解决问题：当 PC＝2PD 时，AD 的长度约为 cm． 2．如图，Q 是 与弦 AB 所围成的图形的内部的一定点，P 是弦 AB 上一动点，连接 PQ 并 第 2页（共 12页） 延长交 于点 C，连接 AC．已知 AB＝6cm，设 A，P 两点间的距离为 xcm，P，C 两点 间的距离为 y1cm，A，C 两点间的距离为 y2cm． 小腾根据学习函数的经验，分别对函数 y1，y2 随自变量 x 的变化而变化的规律进行了探 究． 下面是小腾的探究过程，请补充完整： （1）按照下表中自变量 x 的值进行取点、画图、测量，分别得到了 y1，y2 与 x 的几组对 应值； x/cm 0 1 2 3 4 5 6 y1/cm 5.62 4.67 3.76 2.65 3.18 4.37 y2/cm 5.62 5.59 5.53 5.42 5.19 4.73 4.11 （2）在同一平面直角坐标系 xOy 中，描出补全后的表中各组数值所对应的点（x，y1）， （x，y2），并画出函数 y1，y2 的图象； （3）结合函数图象，解决问题：当△APC 为等腰三角形时，AP 的长度约为 cm． 3．如图，P 是 所对弦 AB 上一动点，过点 P 作 PM⊥AB 交 于点 M，连接 MB，过点 P 作 PN⊥MB 于点 N．已知 AB＝6cm，设 A、P 两点间的距离为 xcm，P、N 两点间的距离 为 ycm．（当点 P 与点 A 或点 B 重合时，y 的值为 0） 第 3页（共 12页） 小东根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行了探究． 下面是小东的探究过程，请补充完整： （1）通过取点、画图、测量，得到了 x 与 y 的几组值，如下表： x/cm 0 1 2 3 4 5 6 y/cm 0 2.0 2.3 2.1 0.9 0 （说明：补全表格时相关数值保留一位小数） （2）建立平面直角坐标系，描出已补全后的表中各对对应值为坐标的点，画出该函数的 图象． （3）结合画出的函数图象，解决问题：当△PAN 为等腰三角形时，AP 的长度约为 cm． 4．已知 y 是 x 的函数，自变量 x 的取值范围 x＞0，下表是 y 与 x 的几组对应值： x … 1 2 3 5 7 9 … y … 1.98 3.95 2.63 1.58 1.13 0.88 … 小腾根据学习函数的经验，利用上述表格所反映出的 y 与 x 之间的变化规律，对该函数 的图象与性质进行了探究． 下面是小腾的探究过程，请补充完整： （1）如图，在平面直角坐标系 xOy 中，描出了以上表格中各对对应值为坐标的点，根据 描出的点，画出该函数的图象； （2）根据画出的函数图象，写出： ① x＝4 对应的函数值 y 约为 ； ② 该函数的一条性质： ． 第 4页（共 12页） 5．有这样一个问题：探究函数 y＝ x2+ 的图象与性质． 小东根据学习函数的经验，对函数 y＝ x2+ 的图象与性质进行了探究． 下面是小东的探究过程，请补充完整： （1）函数 y＝ x2+ 的自变量 x 的取值范围是 ； （2）下表是 y 与 x 的几组对应值． x … ﹣3 ﹣2 ﹣1 ﹣ ﹣ 1 2 3 … y … ﹣ ﹣ ﹣ m … 求 m 的值； （3）如图，在平面直角坐标系 xOy 中，描出了以上表中各对对应值为坐标的点．根据描 出的点，画出该函数的图象； （4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是（1， ），结合函数 的图象，写出该函数的其它性质（一条即可） ． 第 5页（共 12页） 2008～2019 北京中考数学分类汇编(探究性试题之代数篇) 参考答案与试题解析 一．解答题（共 5 小题） 1．如图，P 是 与弦 AB 所围成的图形的外部的一定点，C 是 上一动点，连接 PC 交弦 AB 于点 D． 小腾根据学习函数的经验，对线段 PC，PD，AD 的长度之间的关系进行了探究．下面是 小腾的探究过程，请补充完整： （1）对于点 C 在 上的不同位置，画图、测量，得到了线段 PC，PD，AD 的长度的几 组值，如下表： 位置 1 位置 2 位置 3 位置 4 位置 5 位置 6 位置 7 位置 8 PC/cm 3.44 3.30 3.07 2.70 2.25 2.25 2.64 2.83 PD/cm 3.44 2.69 2.00 1.36 0.96 1.13 2.00 2.83 AD/cm 0.00 0.78 1.54 2.30 3.01 4.00 5.11 6.00 在 PC，PD，AD 的长度这三个量中，确定 AD 的长度是自变量， PD 的长度和 PC 的长度都是这个自变量的函数； （2）在同一平面直角坐标系 xOy 中，画出（1）中所确定的函数的图象； （3）结合函数图象，解决问题：当 PC＝2PD 时，AD 的长度约为 2.3 和 4 cm． 第 6页（共 12页） 【解答】解：（1）根据函数的定义，PC、PD 不可能为自变量，只能是 AD 为自变量 故答案为：AD、PC、PD； （2）描点画出如图图象； （3）PC＝2PD， 从图和表格可以看出位置 4 和位置 6 符合要求， 即 AD 的长度为 2.3 和 4.0． 2．如图，Q 是 与弦 AB 所围成的图形的内部的一定点，P 是弦 AB 上一动点，连接 PQ 并 延长交 于点 C，连接 AC．已知 AB＝6cm，设 A，P 两点间的距离为 xcm，P，C 两点 间的距离为 y1cm，A，C 两点间的距离为 y2cm． 小腾根据学习函数的经验，分别对函数 y1，y2 随自变量 x 的变化而变化的规律进行了探 究． 下面是小腾的探究过程，请补充完整： （1）按照下表中自变量 x 的值进行取点、画图、测量，分别得到了 y1，y2 与 x 的几组对 应值； x/cm 0 1 2 3 4 5 6 y1/cm 5.62 4.67 3.76 3 2.65 3.18 4.37 y2/cm 5.62 5.59 5.53 5.42 5.19 4.73 4.11 （2）在同一平面直角坐标系 xOy 中，描出补全后的表中各组数值所对应的点（x，y1）， （x，y2），并画出函数 y1，y2 的图象； 第 7页（共 12页） （3）结合函数图象，解决问题：当△APC 为等腰三角形时，AP 的长度约为 3 或 4.91 或 5.77 cm． 【解答】解：（1）∵PA＝6 时，AB＝6，BC＝4.37，AC＝4.11， ∴AB2＝AC2+BC2， ∴∠ACB＝90°， ∴AB 是直径． 当 x＝3 时，PA＝PB＝PC＝3， ∴y1＝3， 故答案为 3． （2）函数图象如图所示： （3）观察图象可知：当 x＝y，即当 PA＝PC 或 PA＝AC 时，x＝3 或 4.91， 第 8页（共 12页） 当 y1＝y2 时，即 PC＝AC 时，x＝5.77， 综上所述，满足条件的 x 的值为 3 或 4.91 或 5.77． 故答案为 3 或 4.91 或 5.77． 3．如图，P 是 所对弦 AB 上一动点，过点 P 作 PM⊥AB 交 于点 M，连接 MB，过点 P 作 PN⊥MB 于点 N．已知 AB＝6cm，设 A、P 两点间的距离为 xcm，P、N 两点间的距离 为 ycm．（当点 P 与点 A 或点 B 重合时，y 的值为 0） 小东根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行了探究． 下面是小东的探究过程，请补充完整： （1）通过取点、画图、测量，得到了 x 与 y 的几组值，如下表： x/cm 0 1 2 3 4 5 6 y/cm 0 2.0 2.3 2.1 1.6 0.9 0 （说明：补全表格时相关数值保留一位小数） （2）建立平面直角坐标系，描出已补全后的表中各对对应值为坐标的点，画出该函数的 图象． （3）结合画出的函数图象，解决问题：当△PAN 为等腰三角形时，AP 的长度约为 2.2 cm． 【解答】解：（1）通过取点、画图、测量可得 x＝4 时，y＝1.6cm， 故答案为 1.6． （2）利用描点法，图象如图所示． 第 9页（共 12页） （3）当△PAN 为等腰三角形时， ∵∠APN＞90°， ∴只有 PA＝PN 一种情形，即 x＝y，作出直线 y＝x 与图象的交点坐标为（2.2，2.2）， ∴△PAN 为等腰三角形时，PA＝2.2cm． 故答案为 2.2． 4．已知 y 是 x 的函数，自变量 x 的取值范围 x＞0，下表是 y 与 x 的几组对应值： x … 1 2 3 5 7 9 … y … 1.98 3.95 2.63 1.58 1.13 0.88 … 小腾根据学习函数的经验，利用上述表格所反映出的 y 与 x 之间的变化规律，对该函数 的图象与性质进行了探究． 下面是小腾的探究过程，请补充完整： （1）如图，在平面直角坐标系 xOy 中，描出了以上表格中各对对应值为坐标的点，根据 描出的点，画出该函数的图象； （2）根据画出的函数图象，写出： ① x＝4 对应的函数值 y 约为 2 ； ② 该函数的一条性质： 该函数有最大值 ． 第 10页（共 12页） 【解答】解：（1）如图， （2） ① x＝4 对应的函数值 y 约为 2.0； ② 该函数有最大值． 故答案为 2，该函数有最大值． 5．有这样一个问题：探究函数 y＝ x2+ 的图象与性质． 小东根据学习函数的经验，对函数 y＝ x2+ 的图象与性质进行了探究． 下面是小东的探究过程，请补充完整： （1）函数 y＝ x2+ 的自变量 x 的取值范围是 x≠0 ； （2）下表是 y 与 x 的几组对应值． x … ﹣3 ﹣2 ﹣1 ﹣ ﹣ 1 2 3 … y … ﹣ ﹣ ﹣ m … 求 m 的值； （3）如图，在平面直角坐标系 xOy 中，描出了以上表中各对对应值为坐标的点．根据描 出的点，画出该函数的图象； 第 11页（共 12页） （4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是（1， ），结合函数 的图象，写出该函数的其它性质（一条即可） 该函数没有最大值 ． 【解答】解：（1）x≠0， （2）令 x＝3， ∴y＝ ×32+ ＝ + ＝ ； ∴m＝ ； （3）如图 （4）该函数的其它性质： ① 该函数没有最大值； ② 该函数在 x＝0 处断开； ③ 该函数没有最小值； ④ 该函数图象没有经过第四象限． 故答案为该函数没有最大值． 第 12页（共 12页） 声明：试 题解析著作权 属菁优网所有 ，未经书面同 意，不得复制 发布 日期：2020/1/19 13:50:50 ；用户： 金雨教育；邮 箱：309593466@qq.com ；学号： 335385