八年级下数学课件八年级下册数学课件《三角形的中位线》 北师大版 (8)_北师大版

八年级下数学课件八年级下册数学课件《三角形的中位线》 北师大版 (8)_北师大版

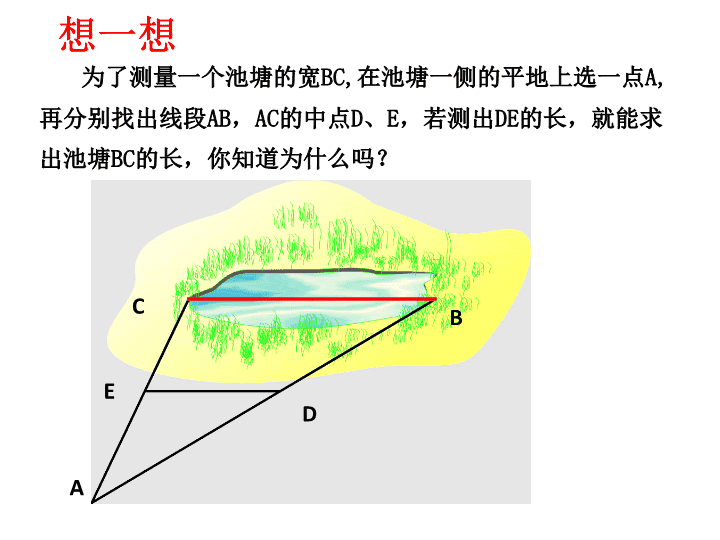
B、C两点被池塘隔开如何测量B、C两点距离？ C B 想一想 A BC D E 为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A, 再分别找出线段AB，AC的中点D、E，若测出DE的长，就能求 出池塘BC的长，你知道为什么吗？ 想一想 A B C D E 合作学习 剪一刀，将一张三角形纸片剪成 一张三角形纸片和一张梯形纸片. （1）要保证剪成一张三角形纸片和一张梯形纸片，剪 痕的位置有什么要求？ （2）若要使△ADE与梯形DBCE能拼成平行四边形， 剪痕的位置有什么要求？ （3）要把所剪得的两个图形拼成 一个平行四边形，可将其中的三角 形作怎样的图形变换？ A B C D E F 连结三角形两边中点的线段叫三角形的中位线 三角形有三条中位线 ∵D、 E分别为AB、AC的中点 ∴DE为△ABC的中位线 三角形的中位线和三角形的中线不同注意 同理DF、EF也为△ ABC的中位线 ED F A CB 三角形的中位线与第三边有什么关系? 三角形的中位线平行且等于第三边的一半 已知：如图，DE是△ABC的中位线. 求证： BCDE 2 1// 证明：如图，以点E为旋转中心，把⊿ADE绕点E， 按顺时针方向旋转180゜，得到⊿CFE A B C D E F 得到⊿CFE，⊿ADE≌⊿CFE. ∴∠ADE=∠F，AD=CF，DE=EF ∴AB∥CF 又∵BD=AD=CF, ∴四边形BCFD是平行四边形 BC 2 1 //DE BC//DF 证明命题：三角形的中位线平行且等于第三边的一半 证明二：如图，延长DE到F， 使EF=DE，连接CF ∴∠ADE=∠F，AD=CF， ∴AB∥CF 又∵BD=AD=CF, ∴四边形BCFD是平行四边形 BC 2 1 //DEBC//DF A B C D E F ∵DE=EF,AE=EC, ∠AED= ∠CEF ∴⊿ADE≌⊿CFE 已知：如图，DE是△ABC的中位线. 求证： BCDE 2 1// A B C ED F 证法三：延长DE到点F，使EF=DE， 连结AF、CF、CD ∵AE=EC∴DE=EF ∴四边形ADCF是平行四边形 ∴AD∥=FC 又D为AB中点，∴DB∥=FC 所以，四边形BCFD是平行四边形  已知：如图，DE是△ABC的中位线. 求证： BCDE 2 1// 证法四：如图，过E作AB的平行线交BC于 F，自A作BC的平行线交FE于G ∵AG∥BC ∴∠EAG=∠ECF ∴△AEG≌△CEF ∴AG=FC，GE=EF 又∵AB∥GF，AG∥BF ∴四边形ABFG是平行四边形 ∴BF=AG=FC，AB=GF 又∵D为AB中点，E为GF中点， ∴DB∥=EF ∴四边形DBFE是平行四边形 ∴DE∥BF，即DE∥BC，DE=BF=FC 即DE=1/2BC A B C ED F G 三角形的中位线平行且等于第三边的一半. 几何语言表述： ∵DE是△ABC的中位线 （或AD=BD,AE=CE) C ED B A BC 2 1 //DE ① 证明平行问题 ② 证明一条线段是另一条线段的两倍或一半 适用范围 1.如图1：在△ABC中，DE是中位线 （1）若∠ADE=60°， 则∠B= 度，为什么？ （2）若BC=8cm， 则DE= cm，为什么？ 2.如图2：在△ABC中，D、E、F分别 是各边中点AB=6cm,AC=8cm,BC=10cm， 则△DEF的周长= cm 60 4 12 图1 AB C D。 。E 图2 B A C D 。 。 E 。F 5 4 3 练一练 三角形三条中位线围成的三角形的周长与原 三角形的周长的关系？ 面积呢？ A BC D E 3、为了测量一个池塘的宽BC,在池塘一侧的平地 上选一点A,再分别找出线段AB，AC的中点D、E， 若测出DE=15m，就能求出池塘BC的长吗？ 练一练 求证：四边形EFGH是平行四边形. A B C D E F G H 证明：如图，连接AC ∵EF是△ABC的中位线 AC 2 1 //EF 同理得： AC 2 1 //GH EF//GH ∴四边形EFGH是平行四边形 ①有中点连线而无三角形,要作辅助线产生三角形 ②有三角形而无中位线,要连结两边中点得中位线 温馨提示： （1） 顺次连结平行四边 形各边中点所得的四边形是 _________？ （2）顺次连结矩形各边中点 所得的四边形是_______？ （3）顺次连结菱形各边中点 所得的四边形是________？ 平行四边形 菱形 矩形 想一想 （4）顺次连结正方 形各边中点所得的四 边形是___________？ （5）顺次连结梯形各边 中点所得的四边形是 ______________？ （6）顺次连结等腰梯形 各边中点所得的四边形 是__________？ 正方形 平行四边形 菱形 想一想 （7）顺次连结对角线相等 的四边形各边中点所得的四 边形是什么？ （9）顺次连结对角线相等且 垂直的四边形各边中点所得 的四边形是什么？ （8）顺次连结对角线垂直 的四边形各边中点所得的四 边形是什么？ 菱形 矩形 正方形 想一想 不相等且不互相垂直的四边形各边中点 组成___________ 对 角 线 平行四边形 互相垂直的四边形各边中点组成______矩形 相等的四边形各边中点组成_____菱形 相等且互相垂直的四边形各边中点 组成_______正方形 共同归纳 1.已知: 如图,DE,EF是⊿ABC的两条中位线.求证: 四边形BFED是平行四边形. 2.如图,DE是⊿ABC的中位线,AF是BC边上的中线,DE 和AF交于点O.求证:DE与AF互相平分. D B CF E A (第1题) F ED CB A O (第2题) 练一练 练一练 3、已知：如图，△ABC是锐角三角形。分别以AB， AC为边向外侧作等边三角形ABM和等边三角形CAN， D，E，F分别是MB，BC，CN的中点，连结DE，FE， 求证：DE=FE A N M F E D CB 方法点拨： 在处理问题时,要求同时出现三角形及中位线 ①有中点连线而无三角形,要作辅助线产生三角形 ②有三角形而无中位线,要连结两边中点得中位线 三角形中位线定理应用： ⑴定理为证明平行关系提供了新的工具 ⑵定理为证明一条线段是另一条线段的2倍或 一半 提供了一个新的途径