- 2021-11-01 发布 |
- 37.5 KB |
- 3页


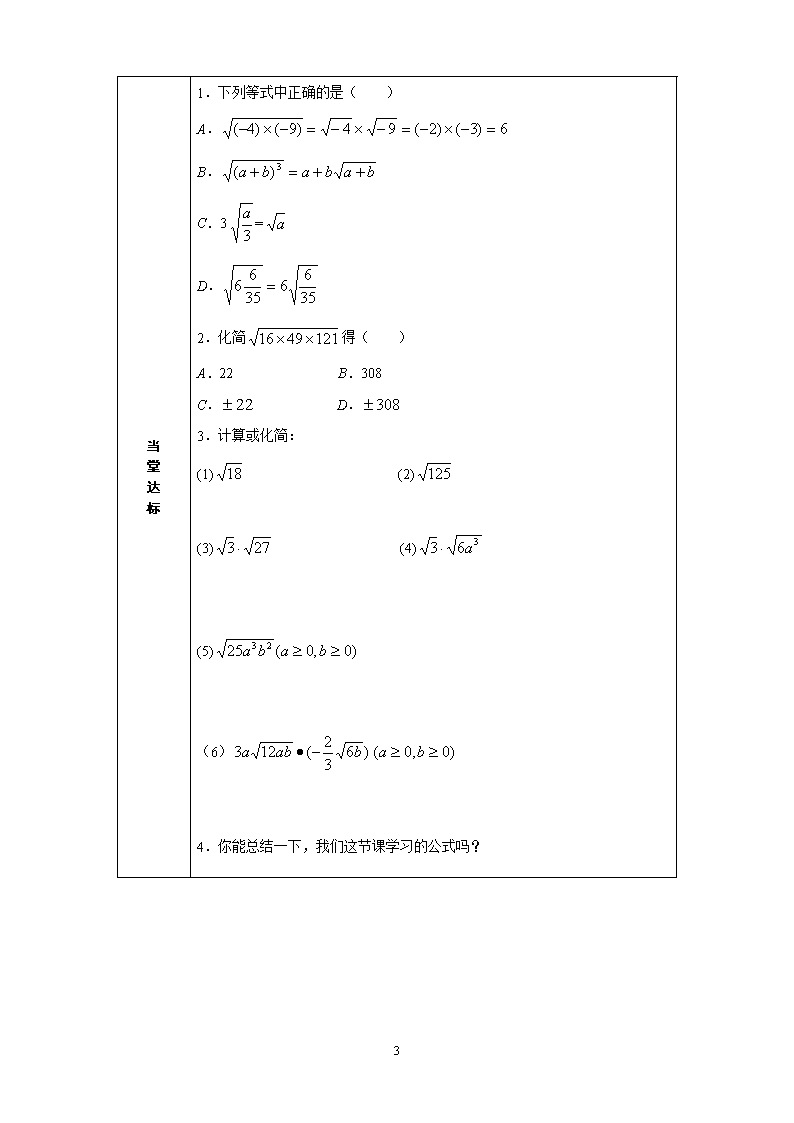
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
二次根式的乘除(1)学案
课题 12.2二次根式的乘除法(1) 学习目标 能利用公式进行二次根式的乘法计算运算或化简; 经历公式的探索过程,体会从特殊到一般的思想方法。 学习重难点 探索二次根式的乘法法则,并运用其进行二次根式的乘法运算或化简。 教学流程 预 习 导 航 (1)与 (2)与 (3)×与 探索 1.学生计算。 2.请同学们观察以上式子及其运算结果,看看其中有什么规律? 3.学生分小组讨论。 4.全班交流。 指名学生回答,其余学生补充。可要求学生举一些类似的式子。 5.概括:一般地,有 = 6.由以上公式逆向运用可得: 文字语言叙述: 积的算术平方根,等于积中各因式的算术平方根的积。 合 作 探 究 一、法则探究: 两个二次根式相乘,把被开方数相乘,根指数不变,即 = 1.注意法则中a、b的符号,这两数均为非负数时,上式才成立; 2.利用这个性质可以化简一些等式,一般地在根式运算的结果中,被开方数应不含有能开得尽方的因数或因式。 二、例题分析: 例1.计算: (1) (2) (3) 3 合 作 探 究 例2.化简: (1), (2), (3); (4) (5)(a≥0,b≥0) 三、展示交流 1.化简:(A级) (1) (2)(a>0) (3) (4) (5) 2.化简:(B级) (1 ) (2) (3) 四、提炼总结 1.概括:一般地,有=.(a≥0,b≥0) 2.由以上公式逆向运用可得: 积的算术平方根,等于积中各因式的算术平方根的积 3.一般地,二次根式的运算结果中,被开方数应不含能开方开得尽方的因数或因式。 4.解决方法: 将被开方数因式分解或因数分解,使出现“完全平方数”或“偶次方因式”) 3 当 堂 达 标 1.下列等式中正确的是( ) A. B. C.3= D. 2.化简得( ) A.22 B.308 C. D. 3.计算或化简: (1) (2) (3) (4) (5) (6) 4.你能总结一下,我们这节课学习的公式吗? 3查看更多